- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Средняя линия треугольника (8 класс)
Содержание
- 1. Презентация по геометрии на тему Средняя линия треугольника (8 класс)
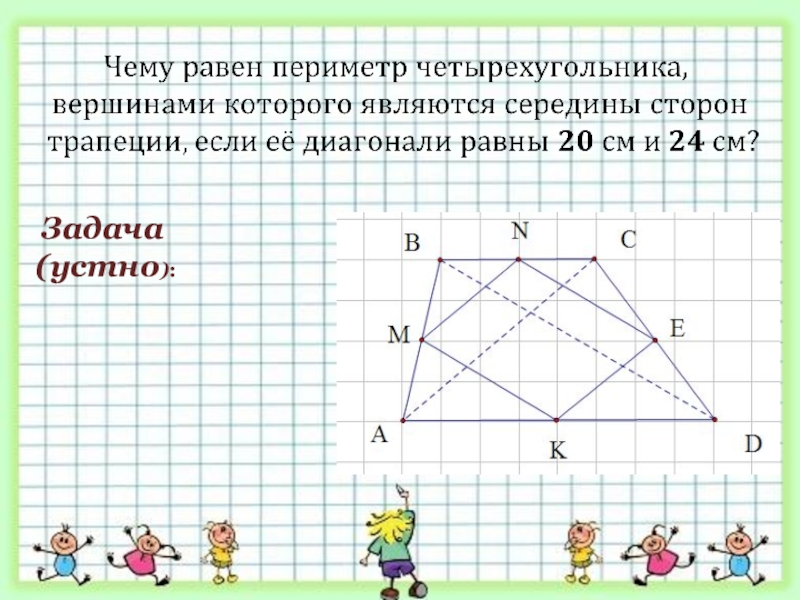
- 2. Задача (устно):
- 3. ЦЕЛИ УРОКА: узнать, что такое средняя линия
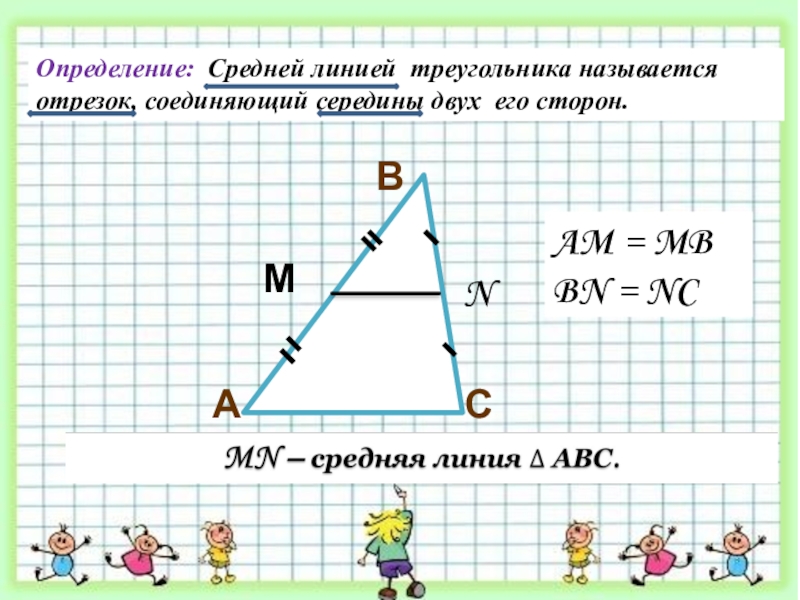
- 4. СВАМNОпределение: Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.AM = MBBN = NC
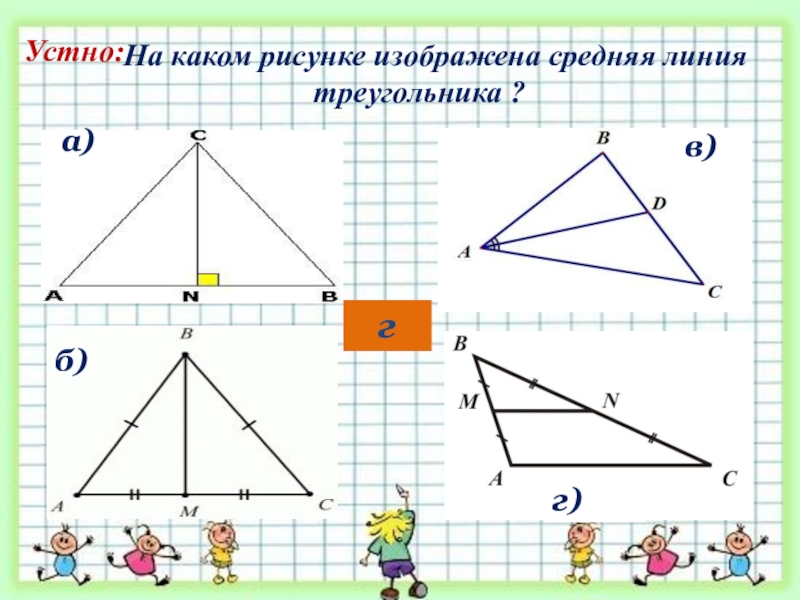
- 5. На каком рисунке изображена средняя линия треугольника ?а)г)б)в)Устно:г
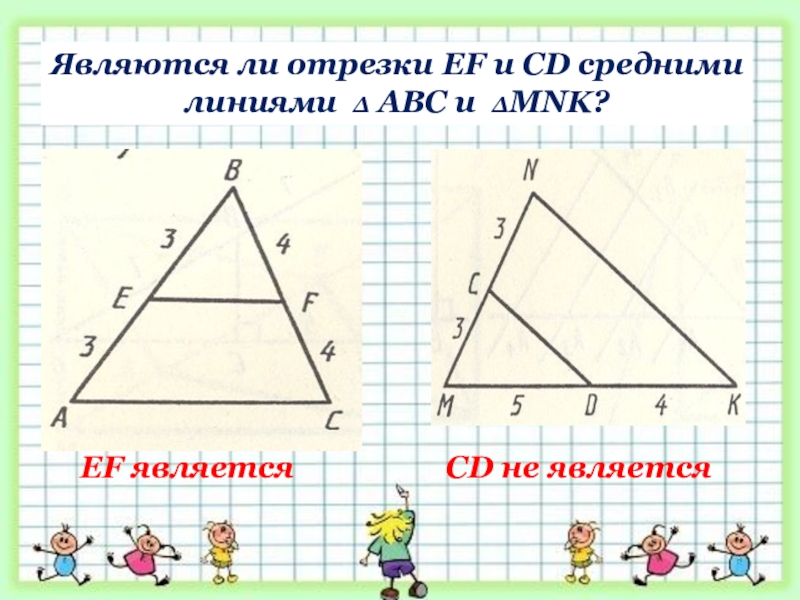
- 6. Являются ли отрезки EF и CD средними линиями ∆ АВС и ∆MNK?EF являетсяCD не является
- 7. На каком рисунке отрезок MN является средней линией треугольника?в)
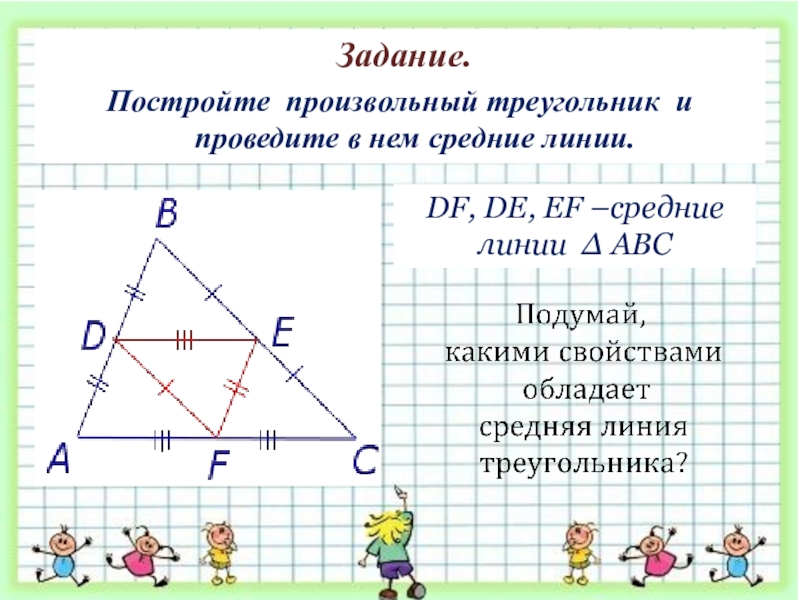
- 8. Задание.Постройте произвольный треугольник и проведите в нем средние линии.DF, DE, EF –средние линии ∆ АВС
- 9. Теорема: Средняя линия треугольника параллельна одной
- 10. Задача 1 ( ГВЭ 2016) - устноСредняя
- 11. Найти
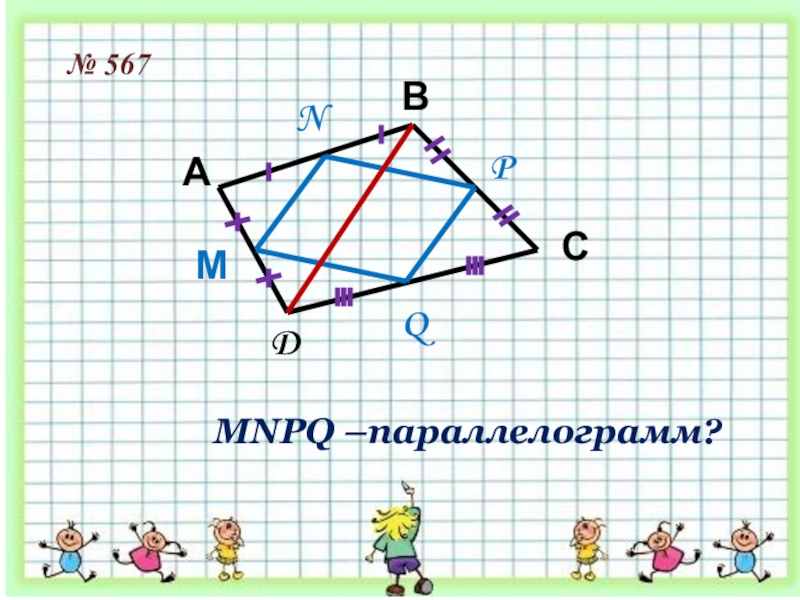
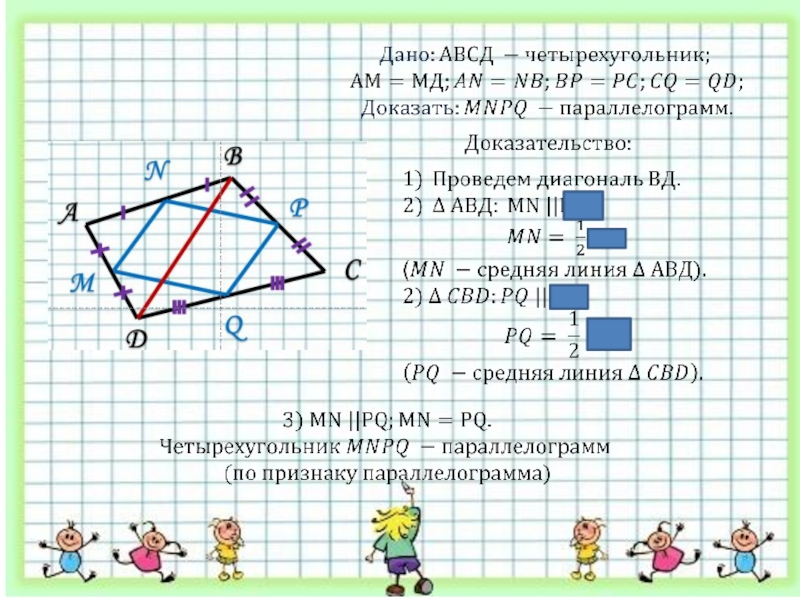
- 12. № 567АВСDМNPQMNPQ –параллелограмм?
- 13. Слайд 13
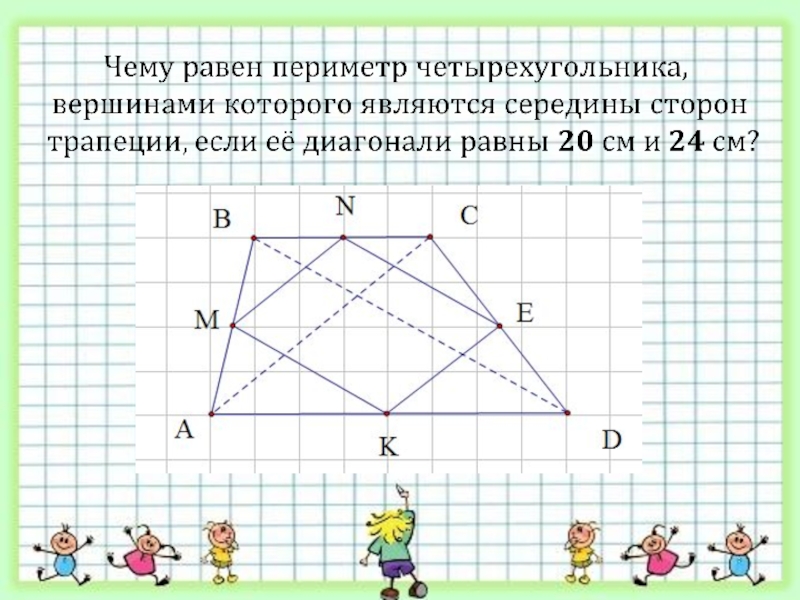
- 14. В XVIII в. французский математик Пьер Вариньон доказал, что
- 15. Слайд 15
- 16. 1. Сколько треугольников вы видите?2. Есть ли
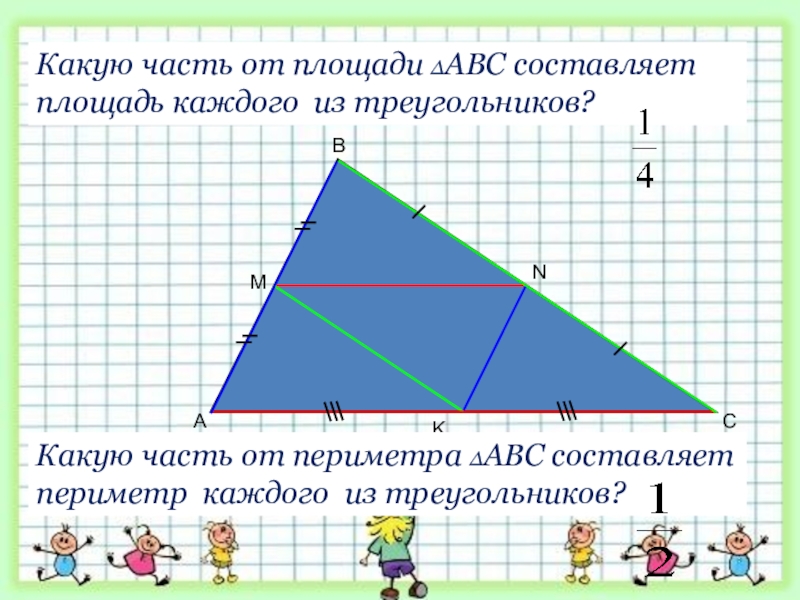
- 17. ABCMKNКакую часть от площади ∆АВС составляет площадь
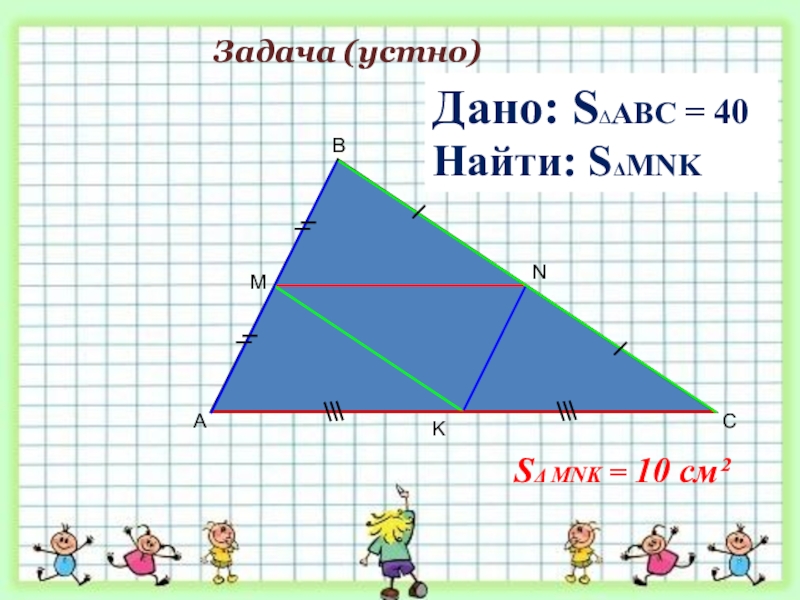
- 18. ABCMДано: S∆ABC = 40 см²Найти: SMNK KN
- 19. Какие новые знания получены на уроке?Что называют средней линией треугольника?Сформулируйте теорему о средней линии треугольника.Подведем итог
- 20. Моё настроение Отличное!Все понятно!Непонятное!Есть над чем подумать…
- 21. п.64 (стр.145), № 565, 566Домашнее задание:
- 22. Спасибо за внимание!!!
Слайд 3ЦЕЛИ УРОКА:
узнать, что такое средняя линия треугольника,
какими свойствами обладает средняя
решать задачи, используя определение и свойство средней линии.
Слайд 4С
В
А
М
N
Определение: Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
AM
BN = NC
Слайд 8 Задание.
Постройте произвольный треугольник и проведите в нем средние линии.
DF, DE,
Слайд 9Теорема: Средняя линия треугольника параллельна одной из его сторон и
С
В
А
М
N
Дано: ΔАВС, МN – средняя линия.
Доказать: МN || АС, МN =½ АС
Доказательство:
2. < 1 = < 2, (соответственные при прямых МN и АС и секущей АВ). Значит, МN || АС.
Слайд 10Задача 1 ( ГВЭ 2016) - устно
Средняя линия равностороннего треугольника АВС
А
В
С
Р ∆ АВС = 48 см
Слайд 11 Найти площадь треугольника, если высота,
Задача 3 ( ГИА 2015 с готовым чертежом)
- устно
Н
S АВС = 50 см²
Слайд 14В XVIII в. французский математик Пьер Вариньон доказал, что середины сторон выпуклого четырёхугольника
Слайд 161. Сколько треугольников вы видите?
2. Есть ли равные треугольники? Почему?
Устно:
3. Сколько
∆ADF, ∆ DBE, ∆ ECF, ∆ DEF, ∆ ABC
∆ADF= ∆ DBE= ∆ ECF= ∆ DEF
ADEF, DBEF, ECFD
Слайд 17A
B
C
M
K
N
Какую часть от площади ∆АВС составляет площадь каждого из треугольников?
Какую часть
Слайд 19Какие новые знания получены на уроке?
Что называют средней линией треугольника?
Сформулируйте теорему
Подведем итог