- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Средняя линия треугольника
Содержание
- 1. Презентация по геометрии на тему Средняя линия треугольника
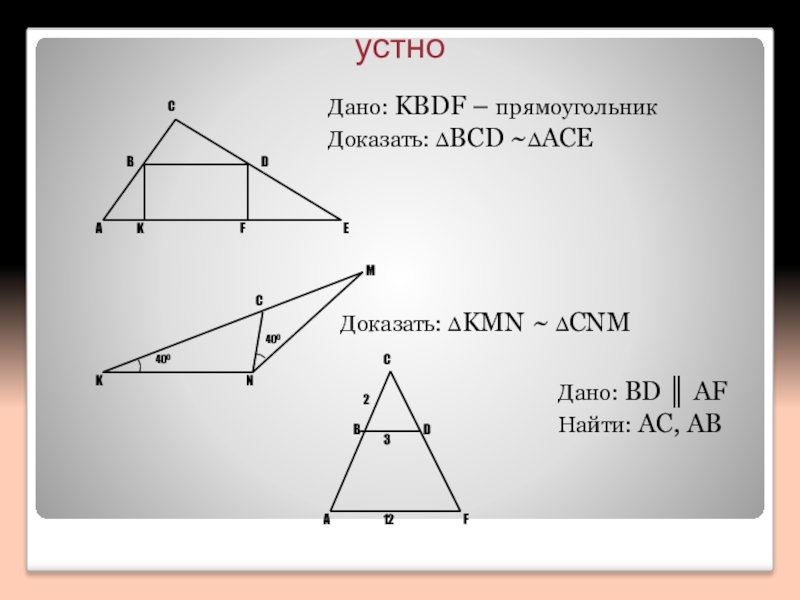
- 2. устно
- 3. Построение средней линии треугольника (1-й способ)Начертите
- 4. Построение средней линии треугольника (2-й способ)Начертите
- 5. Теорема:Средняя линия треугольника параллельна одной из его
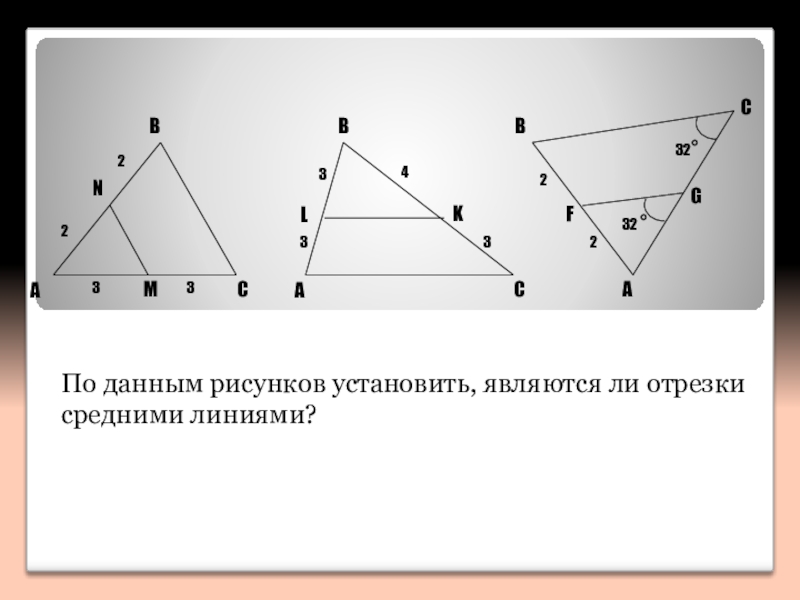
- 6. ABCNM2233ABCLK33432232°32 °ABCFGПо данным рисунков установить, являются ли отрезки средними линиями?
- 7. Решить задачу:Диагональ прямоугольника равна 17 см. Найти периметр четырехугольника, вершинами сторон которого являются середины сторон прямоугольника.
- 8. Задача с практическим применениемНайти длину поля, если
- 9. Итоги урокаКакой отрезок называют средней линией треугольника?Какими
- 10. Домашнее заданиеОтветить на вопросы учебника, стр. 154,
Слайд 3 Построение средней линии треугольника (1-й способ)
Начертите произвольный треугольник ABC
С помощью
Через точку N проведите прямую, параллельную стороне AC
Измерьте длины отрезков BM и MC и сделайте вывод
NM - средняя линия треугольника ABC
N
M
Определение:
Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника.
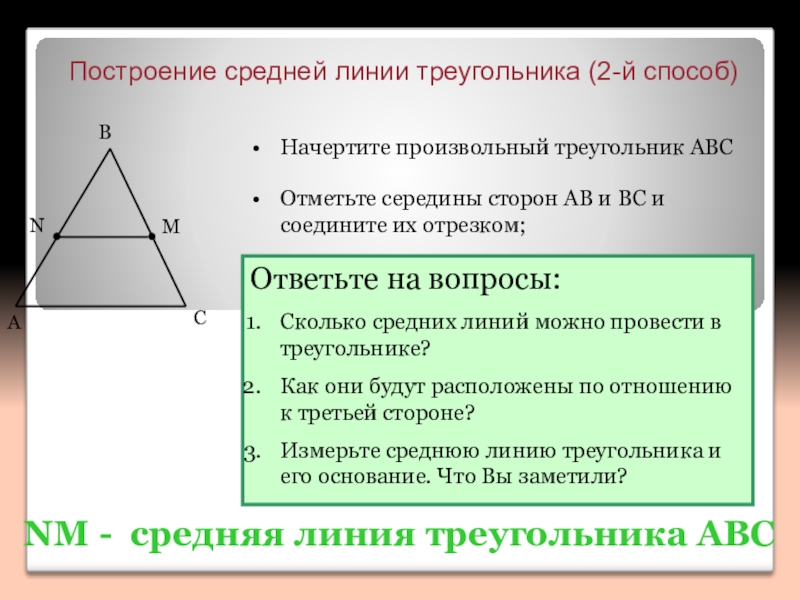
Слайд 4 Построение средней линии треугольника (2-й способ)
Начертите произвольный треугольник ABC
Отметьте середины
NM - средняя линия треугольника ABC
N
M
Ответьте на вопросы:
Сколько средних линий можно провести в треугольнике?
Как они будут расположены по отношению к третьей стороне?
Измерьте среднюю линию треугольника и его основание. Что Вы заметили?
Слайд 5Теорема:
Средняя линия треугольника параллельна одной из его сторон и равна половине
Дано:
∆ABC, M Є BC, N Є AB.
NM-средняя линия.
Доказать:
NM ║ AC, NM = ½ AC
Доказательство:
∆BNM ~ ∆ABC по 2 п.п.т.(LB–общий, BM:BC = BN:BA = ½),
значит L1 = L2 и NM:AC = ½;
Т.е. NM=1/2AC
2. Т.к. L1 = L2 (из подобия треугольников) , а они соответственные при прямых NM и AC и секущей АВ, то NM ║ AC.
Слайд 6A
B
C
N
M
2
2
3
3
A
B
C
L
K
3
3
4
3
2
2
32°
32 °
A
B
C
F
G
По данным рисунков установить, являются ли отрезки средними линиями?
Слайд 7Решить задачу:
Диагональ прямоугольника равна 17 см. Найти периметр четырехугольника, вершинами сторон
Слайд 8Задача с практическим применением
Найти длину поля, если в ней оказалось сто
Слайд 9Итоги урока
Какой отрезок называют средней линией треугольника?
Какими способами можно построить среднюю
Каким свойством обладает средняя линия треугольника?
Где на практике применяется свойство средней линии треугольника?
Ответить на вопросы: