Понятие употребляется для следующих фигур: треугольник, четырёхугольник, трапеция.
Средняя линия треугольника
Средняя линия треугольника
Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника[1].
Свойства
средняя линия треугольника параллельна основанию и равна его половине.
при пересечении всех трёх средних линий образуются 4 равных треугольника, подобных(даже гомотетичных) исходному с коэффициентом 1/2.
средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четвёртой площади исходного треугольника.
Три средние линии треугольника разбивают его на 4 равных (одинаковых) треугольника, подобных исходному треугольнику. Все 4 таких одинаковых треугольника называют серединными треугольниками. Центральный из этих 4 одинаковых треугольников называется дополнительным треугольником.
Признаки
если отрезок параллелен одной из сторон треугольника и соединяет середину одной стороны треугольника с точкой, лежащей на другой стороне треугольника, то это средняя линия.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Средняя линия
Содержание
- 1. Презентация по геометрии на тему Средняя линия
- 2. Средняя линия фигур в планиметрии — отрезок, соединяющий середины
- 3. Средняя линия четырехугольникаСредняя линия четырёхугольника — отрезок, соединяющий середины
- 4. Средняя линия трапецииСредняя линия трапеции — отрезок, соединяющий середины
- 5. Слайд 5
- 6. Слайд 6
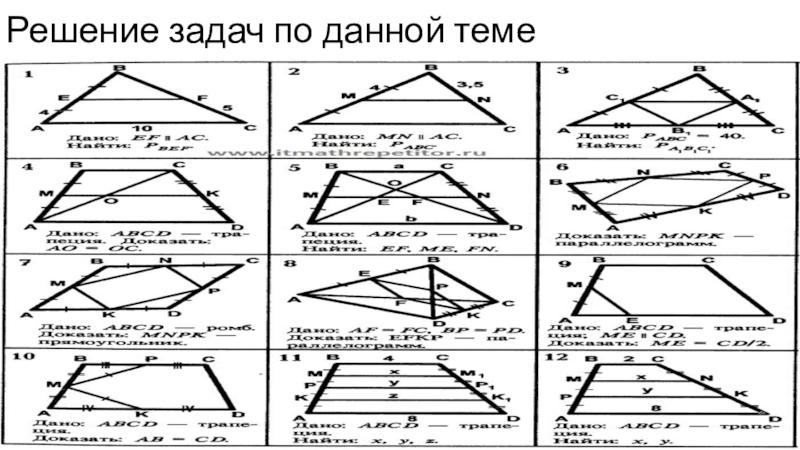
- 7. Основные формулы для решения задач
- 8. Решение задач по данной теме
- 9. Домашняя работаНайдите среднюю линию трапеции, если ее
- 10. До свидания !
Средняя линия фигур в планиметрии — отрезок, соединяющий середины двух сторон данной фигуры. Понятие употребляется для следующих фигур: треугольник, четырёхугольник, трапеция.Средняя линия треугольникаСредняя линия треугольникаСредняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника[1].Свойствасредняя линия треугольника параллельна основанию и равна
Слайд 3Средняя линия четырехугольника
Средняя линия четырёхугольника — отрезок, соединяющий середины противолежащих сторон четырёхугольника.
Свойства
Первая линия
соединяет 2 противоположные стороны. Вторая соединяет 2 другие противоположные стороны. Третья соединяет центры двух диагоналей (не во всех четырёхугольниках диагонали пунктом пересечения делятся пополам).
Если в выпуклом четырёхугольнике средняя линия образует равные углы с диагоналями четырёхугольника, то диагонали равны.
Длина средней линии четырёхугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
Середины сторон произвольного четырёхугольника — вершины параллелограмма. Его площадь равна половине площади четырёхугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона;
Последний пункт означает следующее: В выпуклом четырёхугольнике можно провести четыре средние линии второго рода. Средние линии второго рода - четыре отрезка внутри четырёхугольника, проходящие через середины его смежных сторон параллельно диагоналям. Четыре средние линии второго рода выпуклого четырёхугольника разрезают его на четыре треугольника и один центральный четырёхугольник. Этот центральный четырёхугольник является параллелограммом Вариньона.
Точка пересечения средних линий четырёхугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центроидом вершин четырёхугольника.
В произвольном четырёхугольнике вектор средней линии равен полусумме векторов оснований
Если в выпуклом четырёхугольнике средняя линия образует равные углы с диагоналями четырёхугольника, то диагонали равны.
Длина средней линии четырёхугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
Середины сторон произвольного четырёхугольника — вершины параллелограмма. Его площадь равна половине площади четырёхугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона;
Последний пункт означает следующее: В выпуклом четырёхугольнике можно провести четыре средние линии второго рода. Средние линии второго рода - четыре отрезка внутри четырёхугольника, проходящие через середины его смежных сторон параллельно диагоналям. Четыре средние линии второго рода выпуклого четырёхугольника разрезают его на четыре треугольника и один центральный четырёхугольник. Этот центральный четырёхугольник является параллелограммом Вариньона.
Точка пересечения средних линий четырёхугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центроидом вершин четырёхугольника.
В произвольном четырёхугольнике вектор средней линии равен полусумме векторов оснований
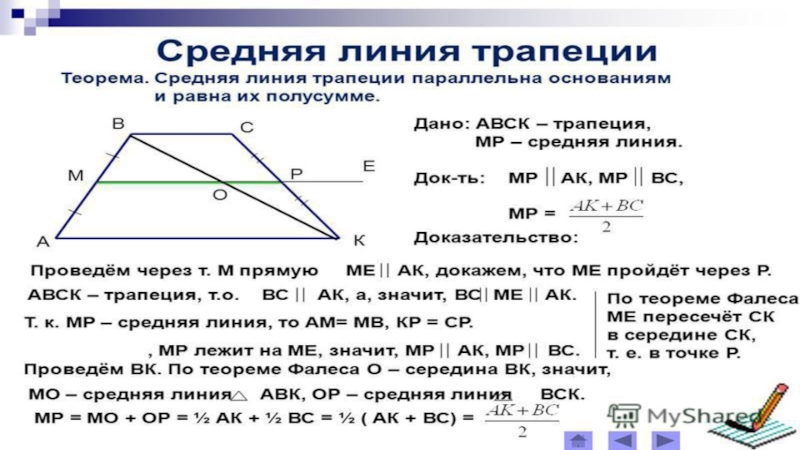
Слайд 4Средняя линия трапеции
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции.
Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.
Она рассчитывается по формуле: EF=AD+BC2, где AD и BC — основания трапеции.
Свойства
средняя линия параллельна основаниям
средняя линия равна полусумме оснований
cредняя линия разбивает фигуру на две трапеции, площади которых соотносятся как [1]
S1/S2=3ВС+AD/BC+3AD
Она рассчитывается по формуле: EF=AD+BC2, где AD и BC — основания трапеции.
Свойства
средняя линия параллельна основаниям
средняя линия равна полусумме оснований
cредняя линия разбивает фигуру на две трапеции, площади которых соотносятся как [1]
S1/S2=3ВС+AD/BC+3AD
Слайд 9Домашняя работа
Найдите среднюю линию трапеции, если ее основания равны 30 и
16.
Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.
Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.