- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Средняя линия треугольника 8 класс решение задач
Содержание
- 1. Презентация по геометрии на тему Средняя линия треугольника 8 класс решение задач
- 2. ОглавлениеСредняя линия треугольникаРешение задач (урок 2)
- 3. Средняя линия треугольникаОпределениеАВСМNСредняя линия треугольника это отрезок
- 4. Средняя линия треугольникаТеоремаВАССредняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.NМ12Доказательство:
- 5. Средняя линия треугольникаТеоремаВАСNМ12
- 6. Средняя линия треугольникаЗадачаУстно №564АВСМNК
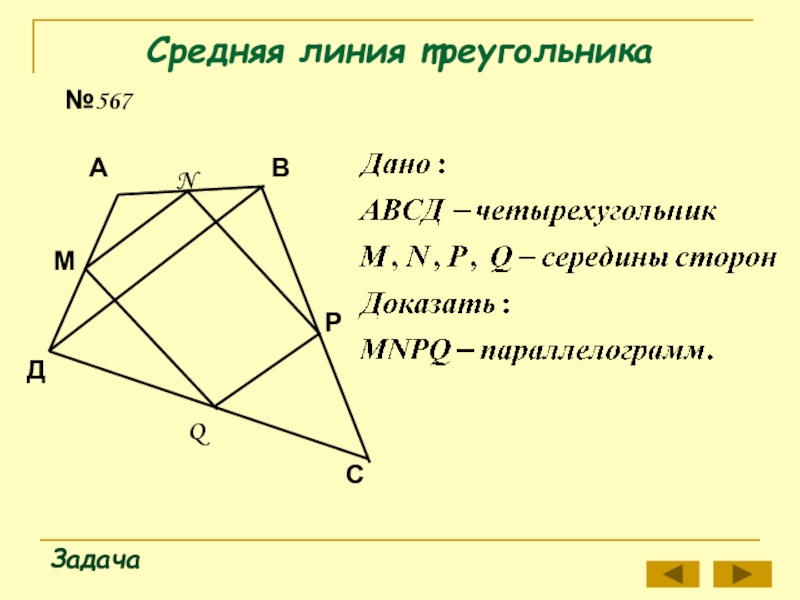
- 7. Средняя линия треугольникаЗадача№567ДАВQМNРС
- 8. Средняя линия треугольникаЗадача№567ДАВQМNРС
- 9. Свойство медиан треугольникаЗадачаМедианы треугольника пересекаются в одной
- 10. Свойство медиан треугольникаЗадачаМедианы треугольника пересекаются в одной
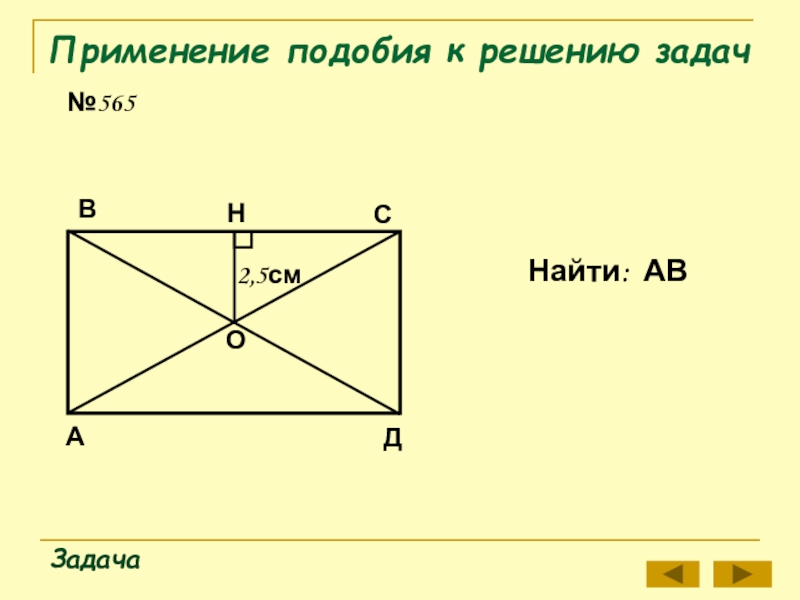
- 11. Применение подобия к решению задач№565ЗадачаНайти: АВ
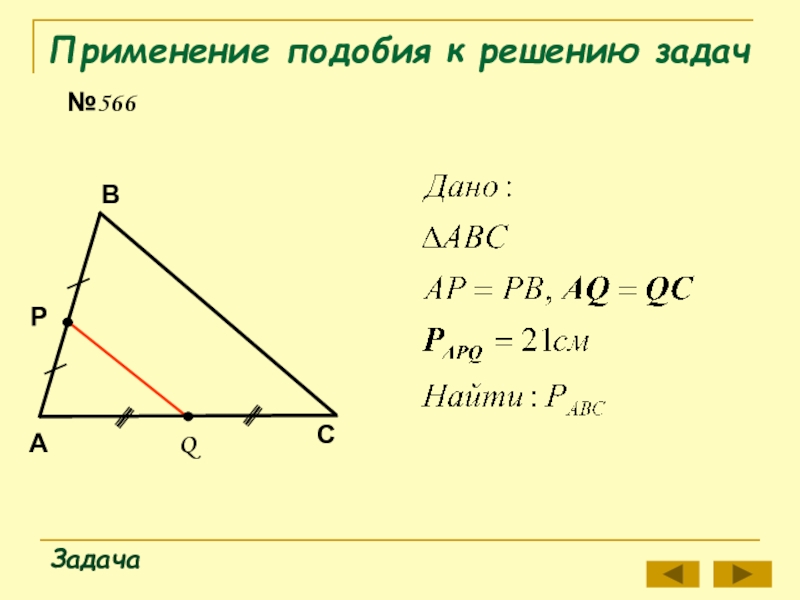
- 12. Применение подобия к решению задач№566ЗадачаАВСРQ
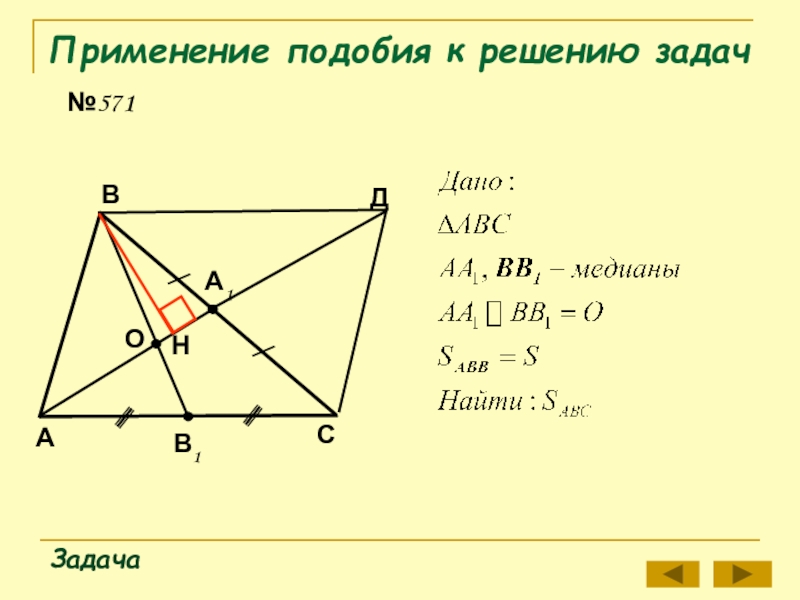
- 13. Применение подобия к решению задач№571ЗадачаОВСВ1А1АДН
- 14. Применение подобия к решению задачУстноЗадачаАВСKMЕF4433NCD3354CDEMN3443Назовите средние линии
- 15. Применение подобия к решению задач2) Сколько средних
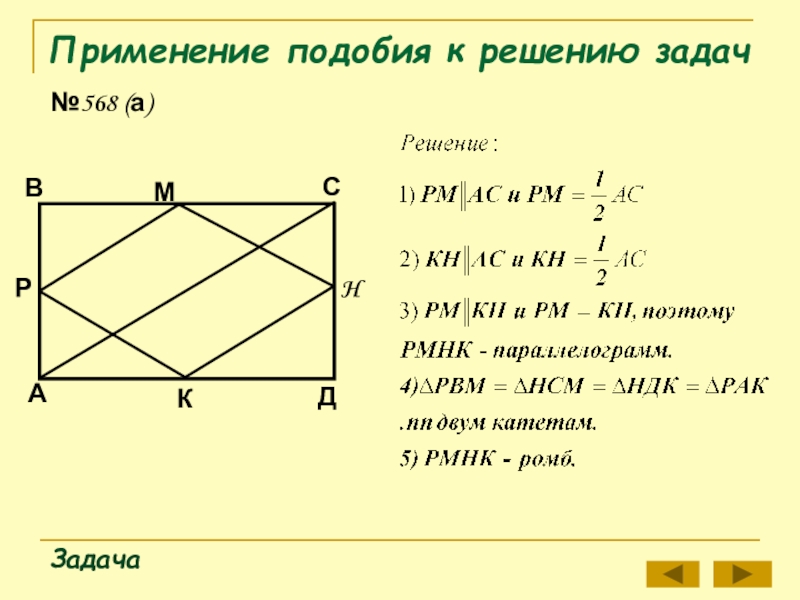
- 16. Применение подобия к решению задач№568 (а)ЗадачаАДКВМСРH
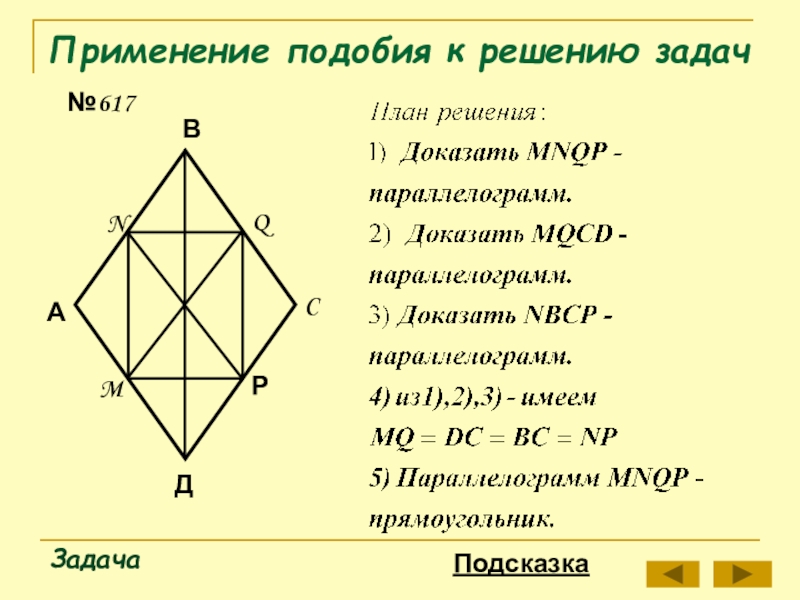
- 17. Применение подобия к решению задач№617ЗадачаАВРNMQCДПодсказка
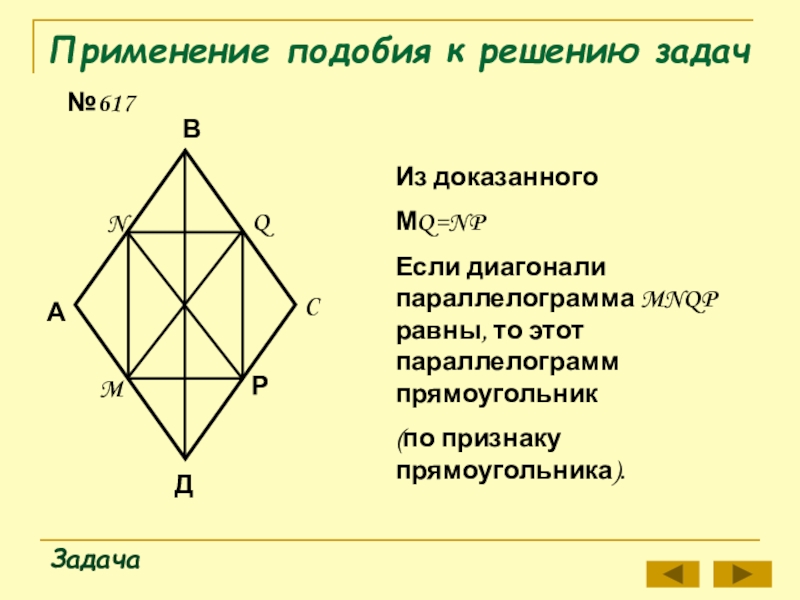
- 18. Применение подобия к решению задач№617ЗадачаАВРNMQCДИз доказанногоМQ=NPЕсли диагонали
- 19. I вариант Площадь ромба 48 см2. Найти
- 20. Л.С. Атанасян «Геометрия7-9» М., Просвещение, 2002.Т.Л. Афанасьева,
ОглавлениеСредняя линия треугольникаРешение задач (урок 2)
Слайд 1Геометрия 8 класс
Средняя линия треугольника
Автор: Бобель Юлия Анатольевна
учитель математики
ГОУ СОШ №313
Фрунзенский район
г. Санкт-Петербург
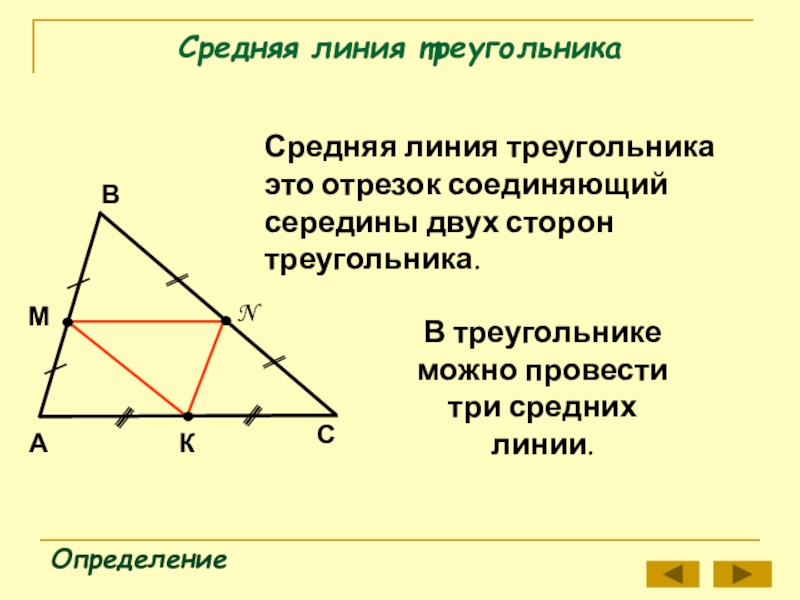
Слайд 3Средняя линия треугольника
Определение
А
В
С
М
N
Средняя линия треугольника это отрезок соединяющий середины двух сторон
треугольника.
В треугольнике можно провести три средних линии.
К
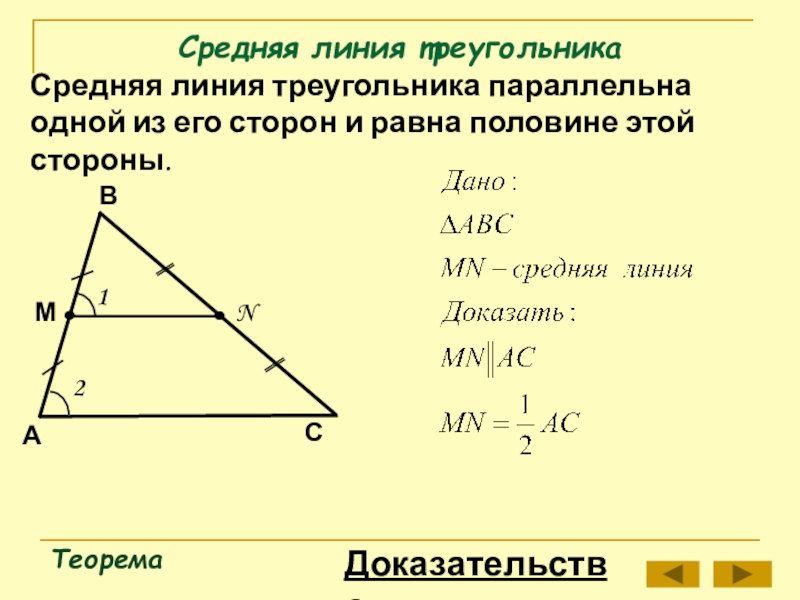
Слайд 4Средняя линия треугольника
Теорема
В
А
С
Средняя линия треугольника параллельна одной из его сторон и
равна половине этой стороны.
N
М
1
2
Доказательство:
Слайд 9Свойство медиан треугольника
Задача
Медианы треугольника пересекаются в одной точке , которая делит
каждую медиану в отношении 2:1, считая от вершины.
А
В
С
А1
В1
C1
Слайд 10Свойство медиан треугольника
Задача
Медианы треугольника пересекаются в одной точке , которая делит
каждую медиану в отношении 2:1, считая от вершины.
А
О
1
3
2
4
Д/З с.154 вопросы 8,9; №565, №566, №571
Слайд 14Применение подобия к решению задач
Устно
Задача
А
В
С
K
M
Е
F
4
4
3
3
N
C
D
3
3
5
4
C
D
E
M
N
3
4
4
3
Назовите средние линии
Слайд 15Применение подобия к решению задач
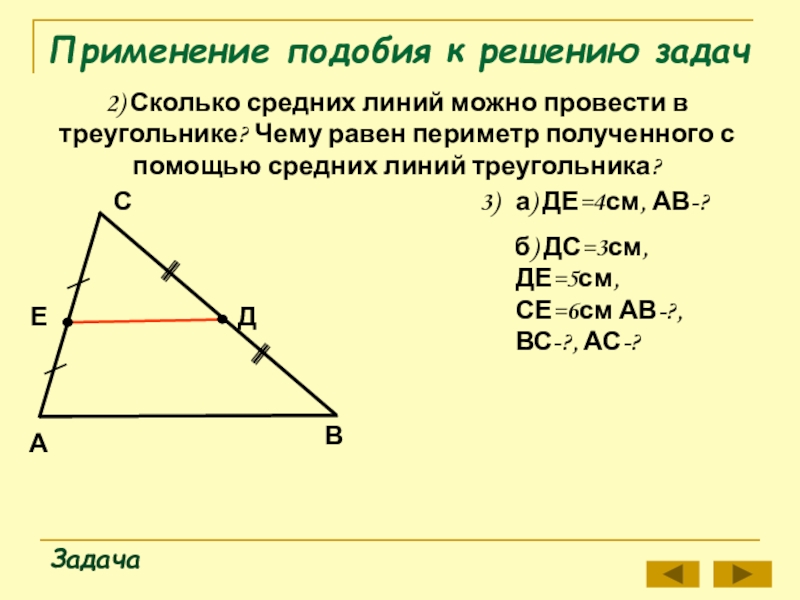
2) Сколько средних линий можно провести в
треугольнике? Чему равен периметр полученного с помощью средних линий треугольника?
Задача
А
В
С
Е
Д
а) ДЕ=4см, АВ-?
б) ДС=3см, ДЕ=5см, СЕ=6см АВ-?, ВС-?, АС-?
Слайд 18Применение подобия к решению задач
№617
Задача
А
В
Р
N
M
Q
C
Д
Из доказанного
МQ=NP
Если диагонали параллелограмма MNQP равны, то
этот параллелограмм прямоугольник
(по признаку прямоугольника).
(по признаку прямоугольника).
Слайд 19I вариант
Площадь ромба 48 см2. Найти площадь четырехугольника, вершинами которого
являются середины сторон данного ромба.
Применение подобия к решению задач
Самостоятельная работа
II вариант
Площадь прямоугольника равна 36 см2. Найти площадь четырехугольника, вершинами которого являются середины сторон данного прямоугольника.
Д/З №568(б), №618
Слайд 20Л.С. Атанасян «Геометрия7-9» М., Просвещение, 2002.
Т.Л. Афанасьева, Л.А. Тапилина Геометрия. 8
класс: Поурочные планы по учебнику Л.С. Атанасяна и др. «Геометрия7-9»
Литература
