:
«Смежные и вертикальные углы»
учителя математики
ГБОУ школы №1056
Романенко Елены Алексеевны
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Смежные и вертикальные углы
Содержание
- 1. Презентация по геометрии на тему Смежные и вертикальные углы
- 2. Смежные углы
- 3. Смежные углы - такие два угла, у
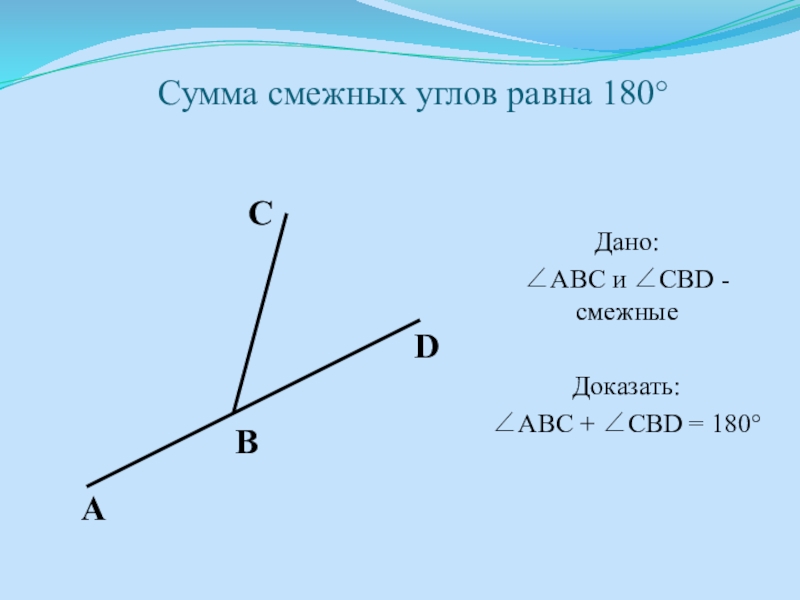
- 4. Сумма смежных углов равна 180Дано:ABC и CBD - смежныеДоказать:ABC + CBD = 180DCAB
- 5. Доказательство:Пусть ABC и CBD – смежные. BC
- 6. Следствия:Если два угла равны, то смежные с
- 7. Задачи для устного решения
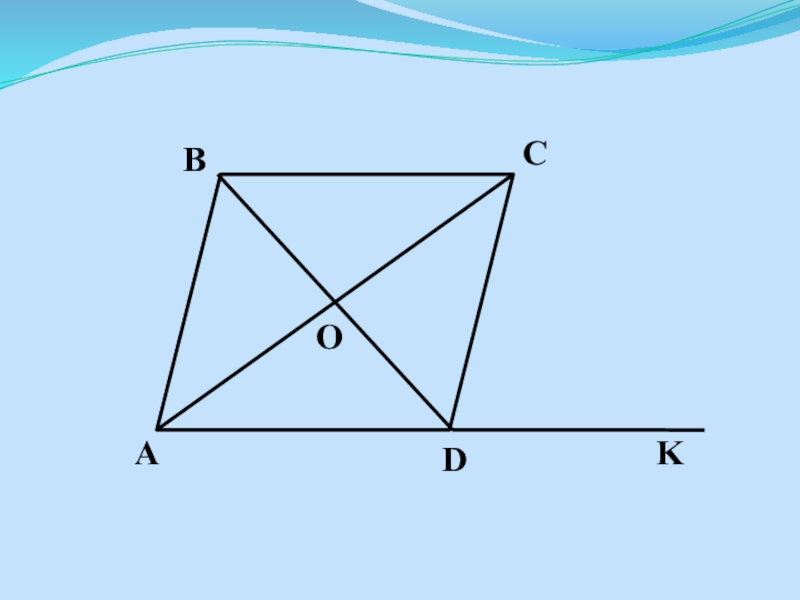
- 8. Найдите на рисунке смежные углы.
- 9. Слайд 9
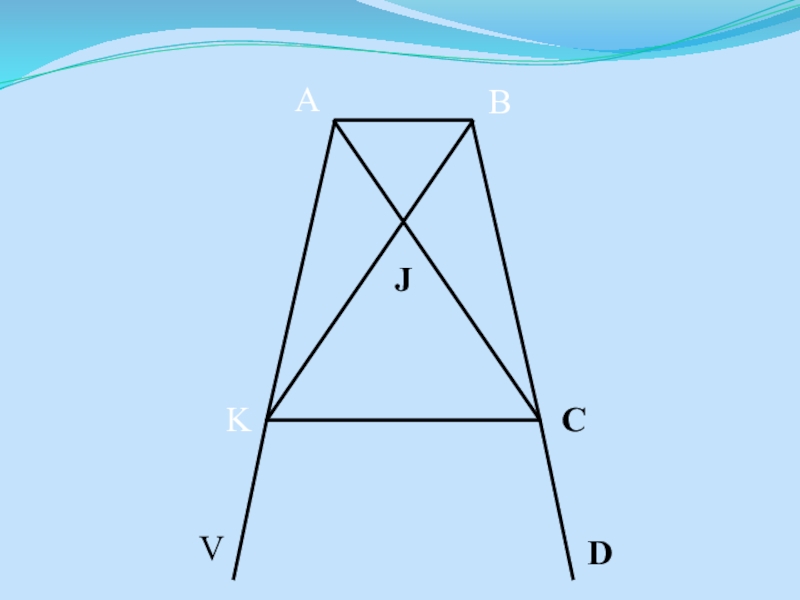
- 10. JCVABKD
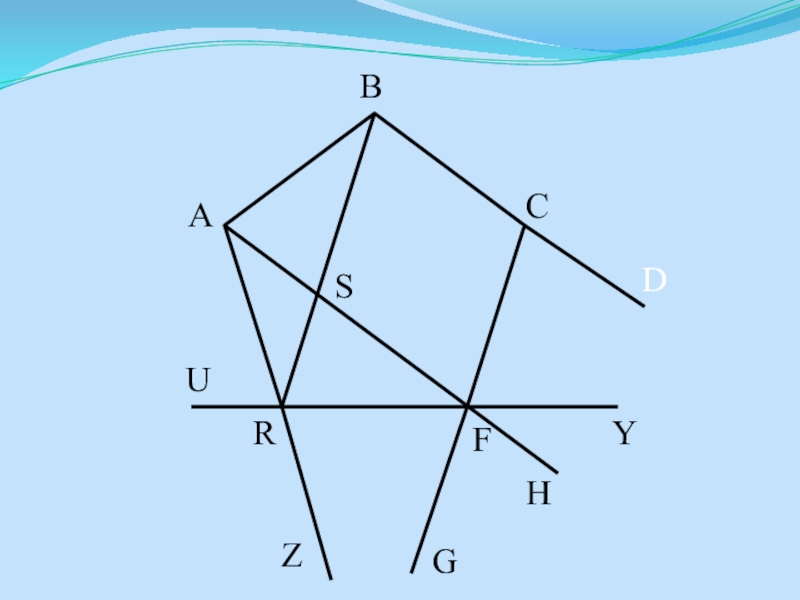
- 11. BZSARFYDGCUH
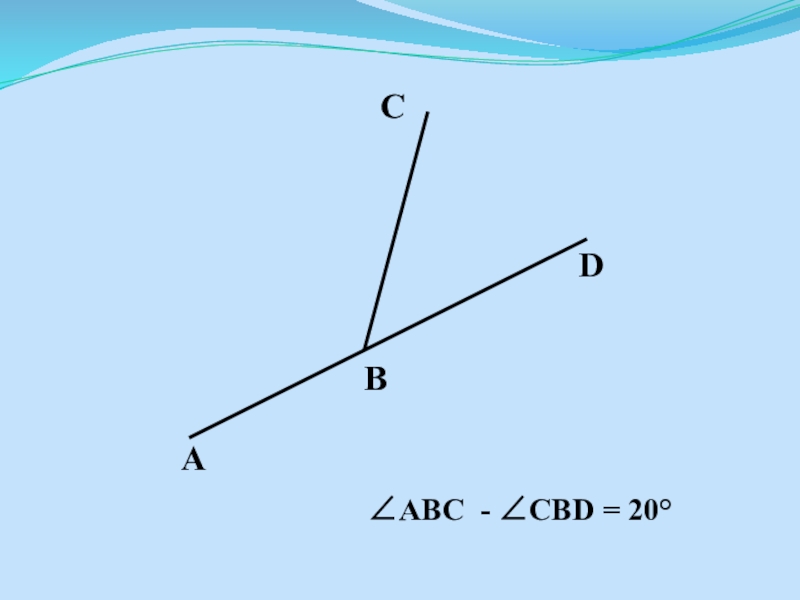
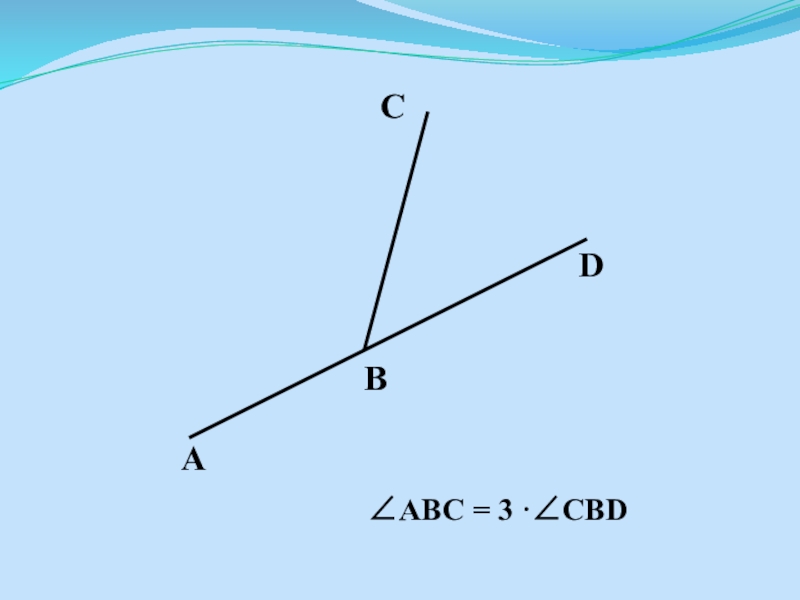
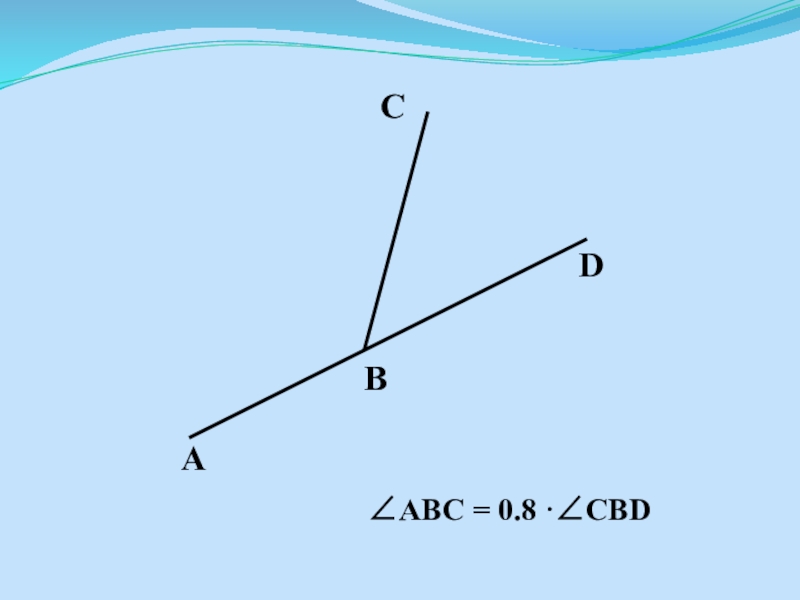
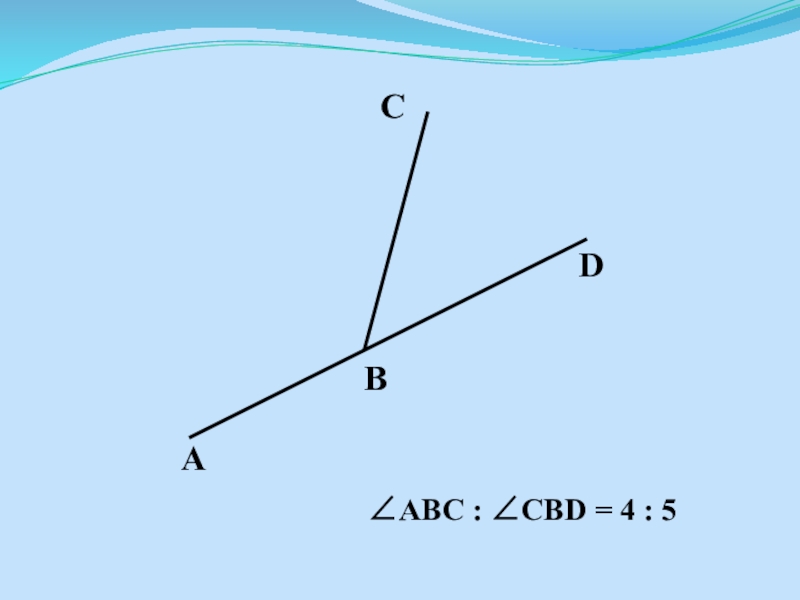
- 12. Найдите углы ABC и CBD.
- 13. ABC - CBD = 20
- 14. ABC = 3 ·CBD
- 15. ABC = 0.8 ·CBD
- 16. ABC : CBD = 4 : 5
- 17. Вертикальные углы
- 18. Вертикальные углы - такие два угла, что
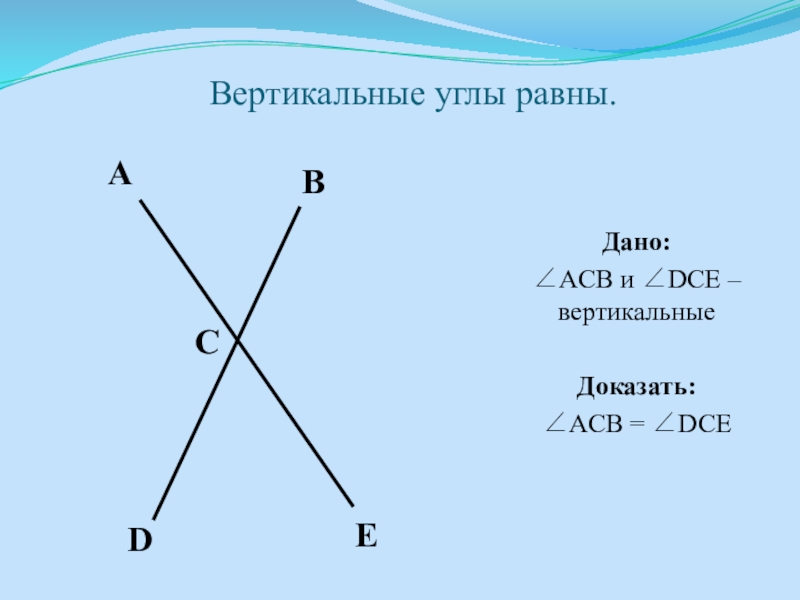
- 19. Вертикальные углы равны.Дано:ACB и DCE – вертикальныеДоказать:ACB = DCEDCABE
- 20. Доказательство:1) Рассмотрим ACB и BCE:
Смежные углы
Слайд 1Департамент образования города Москвы
Северо-Западное окружное управление образования
Презентация по геометрии на тему
Слайд 3Смежные углы -
такие два угла, у которых одна сторона общая,
а другие стороны этих углов являются дополнительными полупрямыми.
D
C
A
B
BC – общая
BA, BD – дополнительные полупрямые
ABC и CBD - смежные
Слайд 5Доказательство:
Пусть ABC и CBD – смежные. BC – луч, проходящий между
сторонами ABD.
ABD = ABC + CBD (аксиома об измерении углов). ABD – развернутый, т.е. ABD = 180
Получаем ABC + CBD = 180
ч.т.д.
ABD = ABC + CBD (аксиома об измерении углов). ABD – развернутый, т.е. ABD = 180
Получаем ABC + CBD = 180
ч.т.д.
Слайд 6Следствия:
Если два угла равны, то смежные с ними углы равны.
Если угол
не развернутый, то его градусная мера меньше 180.
Если один угол прямой, то смежный с ним угол тоже прямой.
Если один угол прямой, то смежный с ним угол тоже прямой.
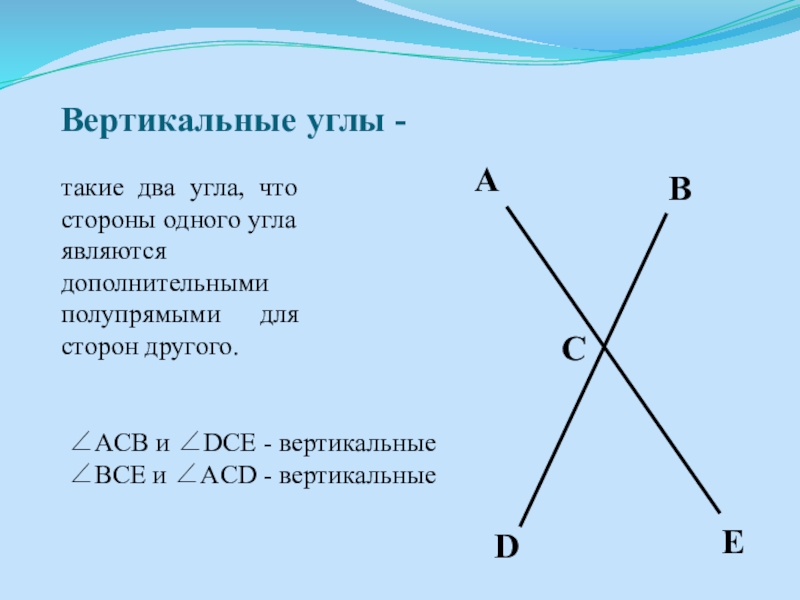
Слайд 18Вертикальные углы -
такие два угла, что стороны одного угла являются
дополнительными полупрямыми для сторон другого.
D
C
A
B
ACB и DCE - вертикальные
BCE и ACD - вертикальные
E
Слайд 20Доказательство:
1) Рассмотрим ACB и BCE: смежные, а значит
ACB +
BCE = 180 (по теореме о смежных углах).
ACB =180 - BCE
2) Рассмотрим BCE и DCE: смежные, а значит
DCE + BCE = 180 (по теореме о смежных углах).
DCE =180 - BCE
3) ACB =180 - BCE
DCE =180 - BCE => ACB = DCE
ч.т.д.
ACB =180 - BCE
2) Рассмотрим BCE и DCE: смежные, а значит
DCE + BCE = 180 (по теореме о смежных углах).
DCE =180 - BCE
3) ACB =180 - BCE
DCE =180 - BCE => ACB = DCE
ч.т.д.