Презентация, доклад по геометрии на тему Синус, косинус и тангенс угла (9 класс)

Содержание

Соотношения в прямоугольном треугольникеСинусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузеКосинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузеТангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему

Слайд 1Синус, косинус и тангенс угла

Синус, косинус и тангенс угла

Слайд 2Соотношения в прямоугольном треугольнике
Синусом острого угла прямоугольного треугольника называется отношение противолежащего

катета к гипотенузе

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему

Соотношения в прямоугольном треугольникеСинусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузеКосинусом острого угла прямоугольного

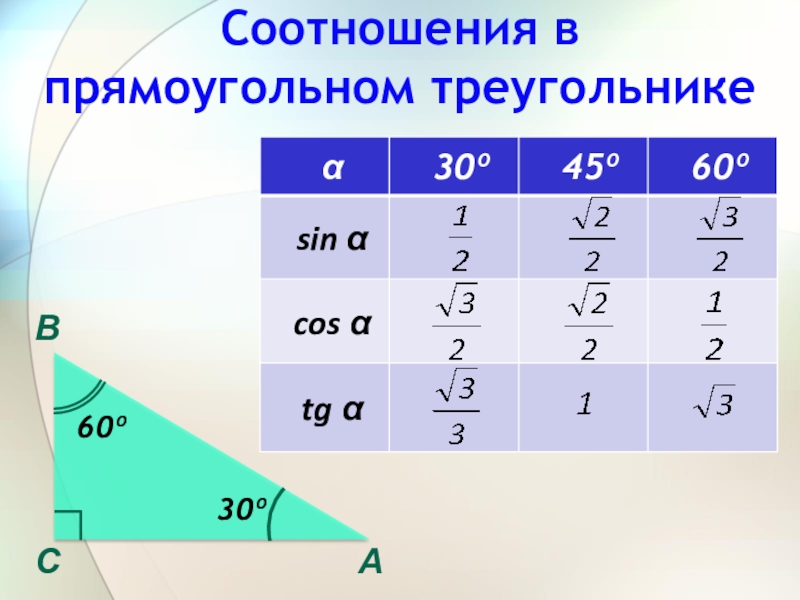
Слайд 3Соотношения в прямоугольном треугольнике

Соотношения в прямоугольном треугольнике

Слайд 4Основное тригонометрическое тождество

Основное тригонометрическое тождество

Слайд 5Соотношения в прямоугольном треугольнике
60º
30º

Соотношения в прямоугольном треугольнике60º30º

Слайд 6Единичная окружность
x
y
1
-1
-1
1
M
N
P
K
0

Единичная окружностьxy1-1-11MNPK0

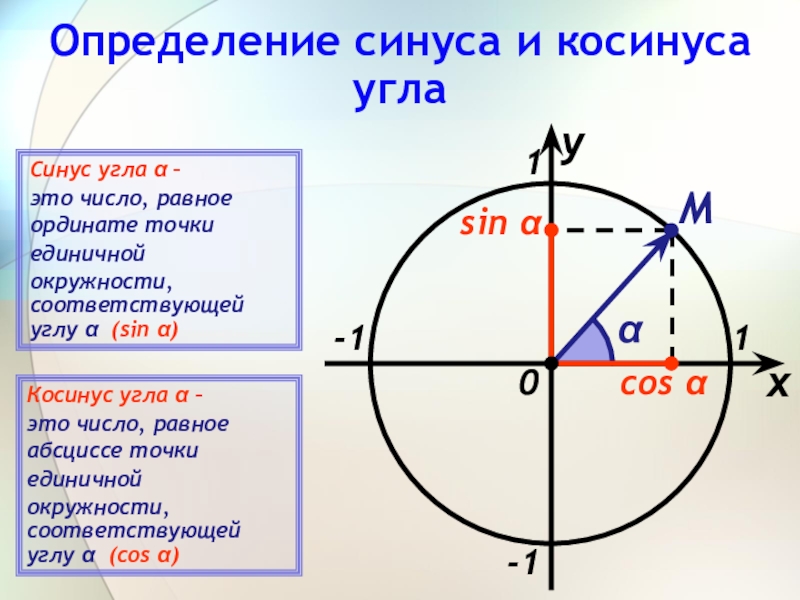
Слайд 7Определение синуса и косинуса угла
x
y
1
-1
-1
1
M
0
sin α
Синус угла α –
это число,

равное ординате точки
единичной
окружности, соответствующей углу α (sin α)

Косинус угла α –
это число, равное абсциссе точки
единичной
окружности, соответствующей углу α (cos α)

α

cos α

Определение синуса и косинуса углаxy1-1-11M0sin αСинус угла α – это число, равное ординате точки единичнойокружности, соответствующей углу

Слайд 8Основное тригонометрическое тождество (1)
x
1
-1
-1
1
M
0
α
sin 2α + cos 2α = 1
x2 +

y 2 = 1

y

x

y

x = ОM ∙ cos α = cos α

y = ОM ∙ sin α = sin α

Основное тригонометрическое тождество (1)x1-1-11M0αsin 2α + cos 2α = 1x2 + y 2 = 1yxyx = ОM

Слайд 9Формулы приведения
sin (90° – α) = cos α
cos (90° – α)

= sin α

sin (180° – α) = sin α

cos (180° – α) = – cos α

Формулы приведенияsin (90° – α) = cos αcos (90° – α) = sin αsin (180° – α)

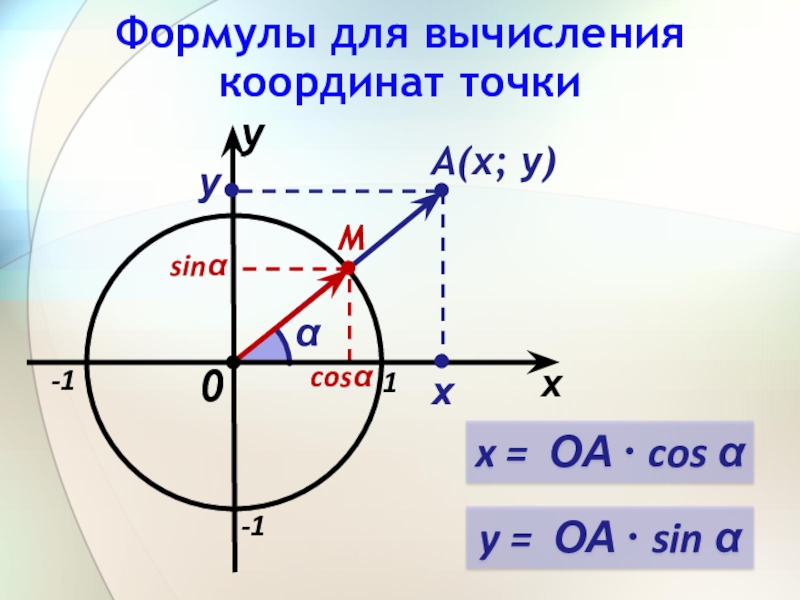
Слайд 10Формулы для вычисления координат точки
x
1
-1
-1
А(х; у)
0
α
y
cosα
sinα
x = ОА ∙ cos α
y

= ОА ∙ sin α

х

y

M

Формулы для вычисления координат точкиx1-1-1А(х; у)0αycosαsinαx = ОА ∙ cos αy = ОА ∙ sin αхyM
Скачать презентацию

Похожие презентации

Центральные и вписанные углы геометрия 8 класс Центральные и вписанные углы геометрия 8 класс 268
Презентация по теме Пифагор и его школа ученицы 8 класса Рябовой Марины Презентация по теме Пифагор и его школа ученицы 8 класса Рябовой Марины 208
Презентация по математике: Параллельность прямых и плоскостей Презентация по математике: Параллельность прямых и плоскостей 239
Презентация к уроку по геометрии на тему Симметрия (8 класс) Презентация к уроку по геометрии на тему Симметрия (8 класс) 415
Презентация к уроку Практическое применение теоремы Пифагора Презентация к уроку Практическое применение теоремы Пифагора 194
Гл.2. Урок 11. Теорема, обратная теореме Пифагора Гл.2. Урок 11. Теорема, обратная теореме Пифагора 206

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Яндекс.Метрика

Обратная связь

Email: Нажмите что бы посмотреть