- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Симметрия
Содержание
- 1. Презентация по геометрии на тему Симметрия
- 2. Движение -преобразование,
- 3. СИММЕТРИЯ - (греч.)
- 4. «Симметрия является той идеей, посредством которой
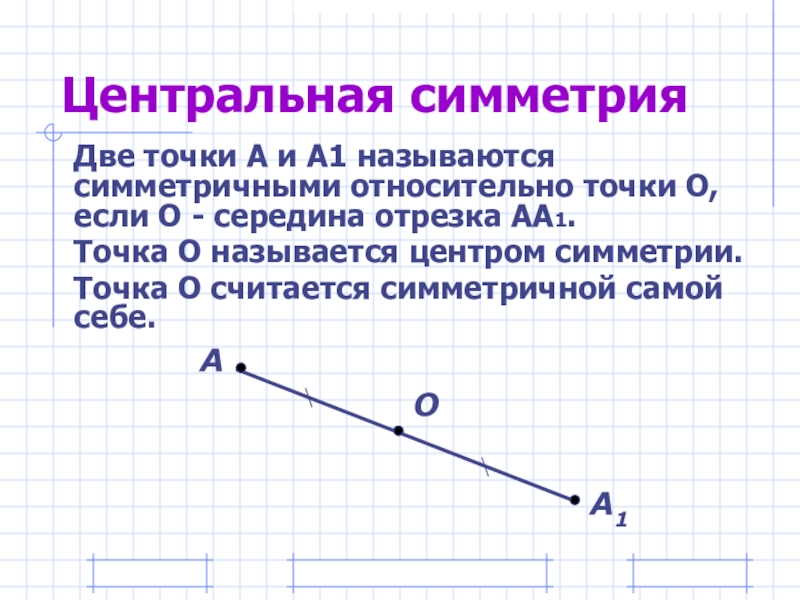
- 5. Центральная симметрияДве точки А и А1 называются
- 6. Центральная симметрияСимметрия относительно точки (центральная симметрия) –
- 7. Слайд 7
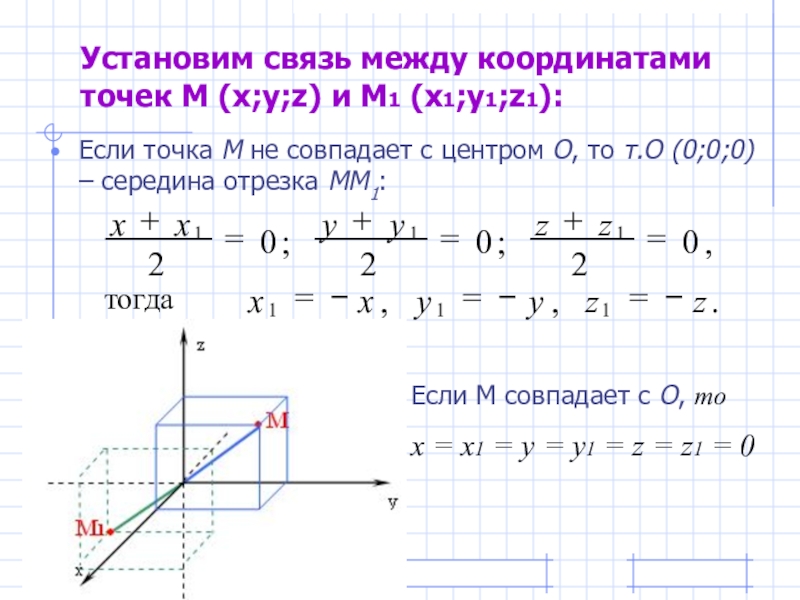
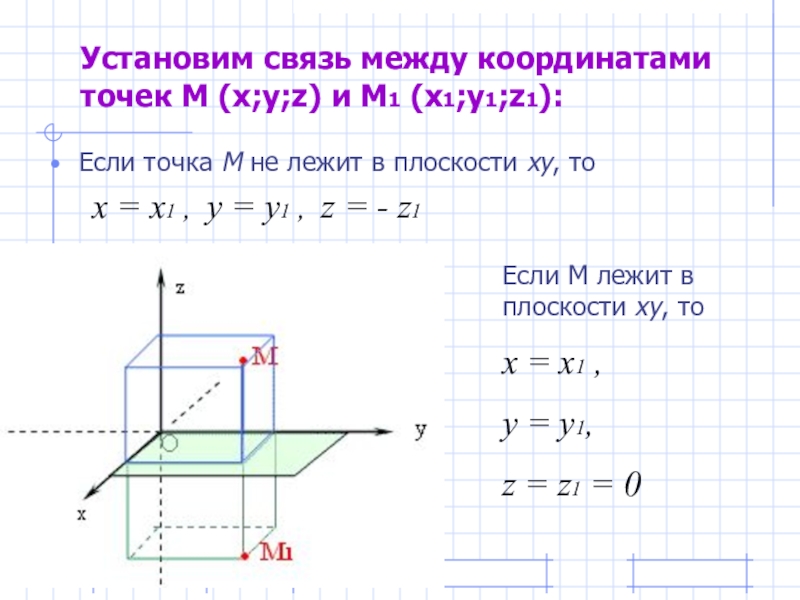
- 8. Установим связь между координатами точек М (x;y;z)
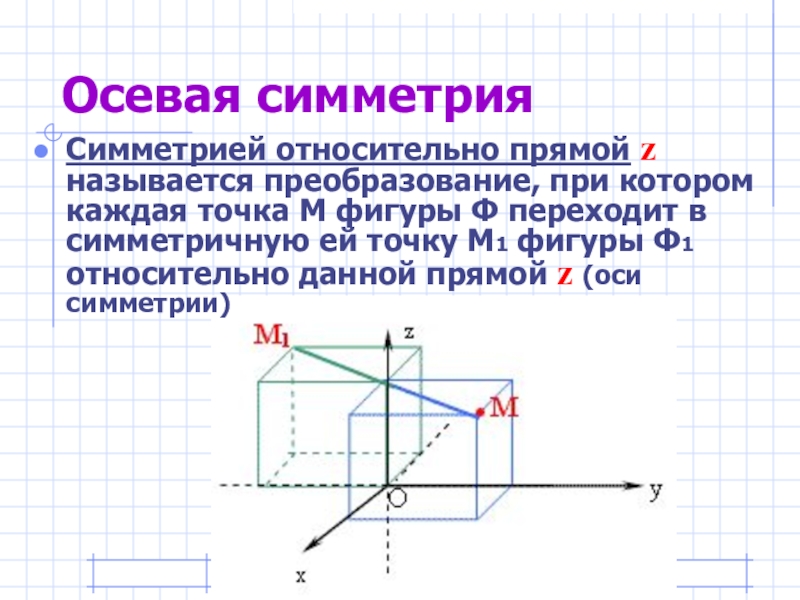
- 9. Осевая симметрияДве точки А и А1 называются
- 10. Осевая симметрияСимметрией относительно прямой z называется преобразование,
- 11. Слайд 11
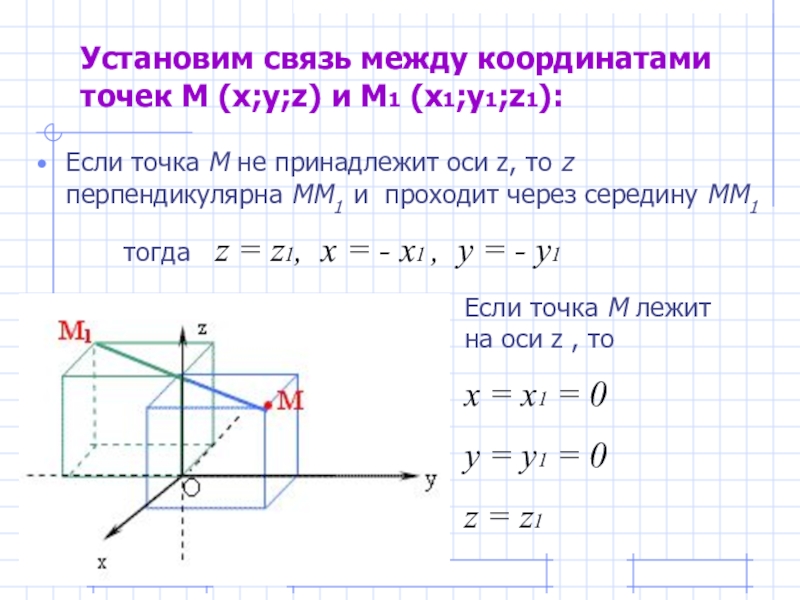
- 12. Установим связь между координатами точек М (x;y;z)
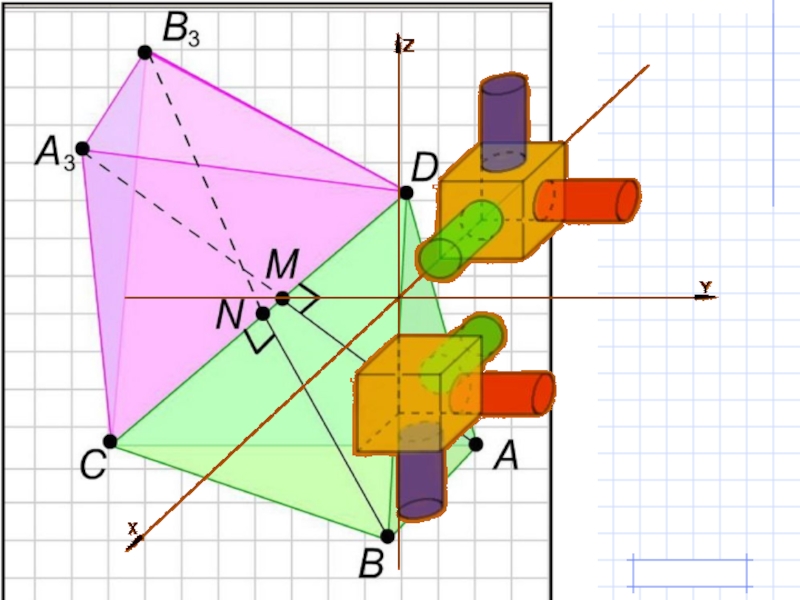
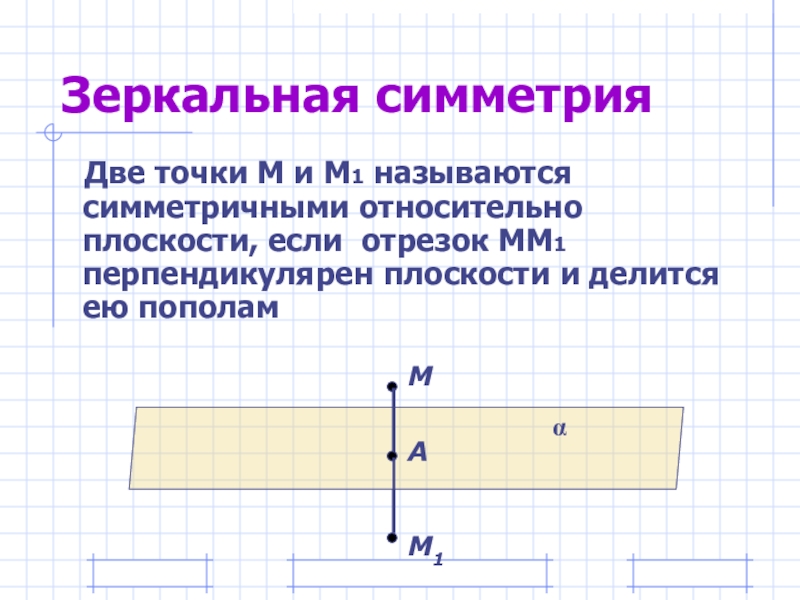
- 13. Зеркальная симметрия Две точки М и М1 называются
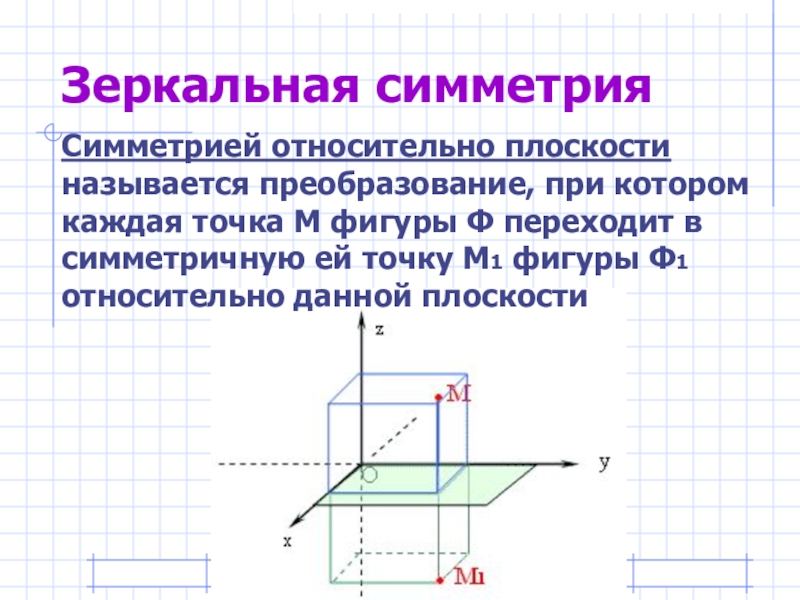
- 14. Зеркальная симметрияСимметрией относительно плоскости называется преобразование, при
- 15. Слайд 15
- 16. Установим связь между координатами точек М (x;y;z)
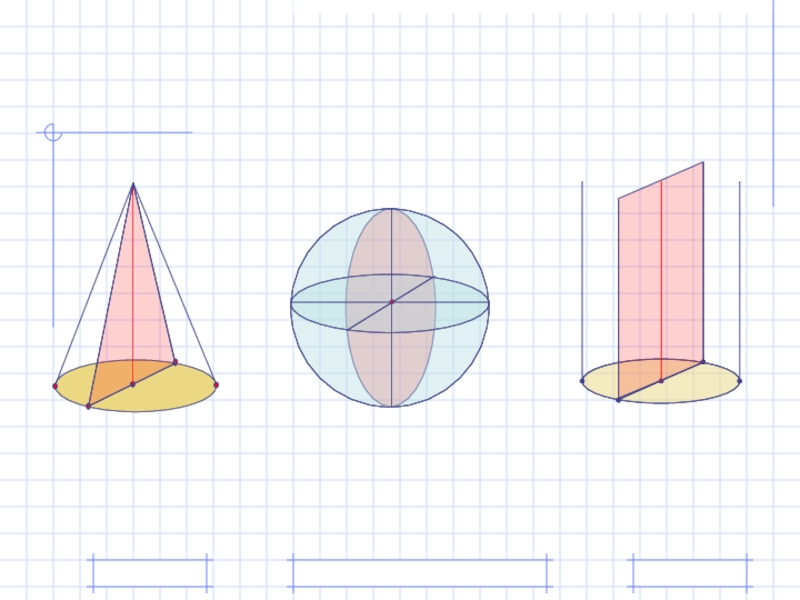
- 17. Фигуры, обладающие симметрией
- 18. Слайд 18
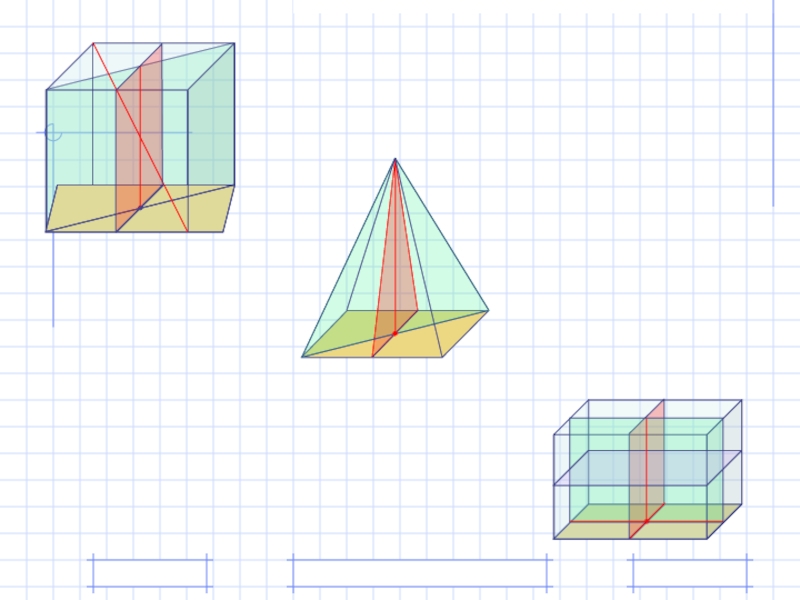
- 19. Фигуры, обладающие симметрией
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. При центральной симметрии относительно точки О (0;0;0)
- 25. При осевой симметрии относительно оси Ох:х1 =
- 26. При зеркальной симметрии относительно плоскости zy:
Движение -преобразование, при котором сохраняются расстояния между точками
Слайд 4 «Симметрия является той идеей, посредством которой
человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство»
(Герман Вейль)
(Герман Вейль)
Слайд 5Центральная симметрия
Две точки А и А1 называются симметричными относительно точки О,
если О - середина отрезка АА1.
Точка О называется центром симметрии.
Точка О считается симметричной самой себе.
Точка О называется центром симметрии.
Точка О считается симметричной самой себе.
О
А1
А
Слайд 6Центральная симметрия
Симметрия относительно точки (центральная симметрия) – преобразование, при котором каждая
точка М фигуры Ф переходит в симметричную ей точку М1 фигуры Ф1 относительно точки О (центра симметрии)
Слайд 8Установим связь между координатами точек М (x;y;z) и М1 (x1;y1;z1):
Если точка
М не совпадает с центром О, то т.О (0;0;0) – середина отрезка ММ1:
Если М совпадает с О, то
х = х1 = у = у1 = z = z1 = 0
Слайд 9Осевая симметрия
Две точки А и А1 называются симметричными относительно прямой а,
если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе
А
А1
а
Слайд 10Осевая симметрия
Симметрией относительно прямой z называется преобразование, при котором каждая точка
М фигуры Ф переходит в симметричную ей точку М1 фигуры Ф1 относительно данной прямой z (оси симметрии)
Слайд 12Установим связь между координатами точек М (x;y;z) и М1 (x1;y1;z1):
Если точка
М не принадлежит оси z, то z перпендикулярна ММ1 и проходит через середину ММ1
Если точка М лежит на оси z , то
х = х1 = 0
у = у1 = 0
z = z1
тогда z = z1, х = - х1 , у = - у1
Слайд 13Зеркальная симметрия
Две точки М и М1 называются симметричными относительно плоскости, если
отрезок ММ1 перпендикулярен плоскости и делится ею пополам
М
М1
α
А
Слайд 14Зеркальная симметрия
Симметрией относительно плоскости называется преобразование, при котором каждая точка М
фигуры Ф переходит в симметричную ей точку М1 фигуры Ф1 относительно данной плоскости
Слайд 16Установим связь между координатами точек М (x;y;z) и М1 (x1;y1;z1):
Если точка
М не лежит в плоскости ху, то
Если М лежит в плоскости ху, то
х = х1 ,
у = у1,
z = z1 = 0
х = х1 , у = у1 , z = - z1
Слайд 17Фигуры,
обладающие симметрией
Осевой
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
Прямая а называется осью симметрии фигуры.
Говорят также, что фигура обладает осевой симметрией
Прямая а называется осью симметрии фигуры.
Говорят также, что фигура обладает осевой симметрией
Центральной
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
Точка О называется центром симметрии фигуры.
Говорят также, что фигура обладает центральной симметрией
Слайд 19Фигуры, обладающие симметрией
Зеркальной
Фигура называется симметричной относительно , если для каждой точки фигуры симметричная ей точка относительно также принадлежит этой фигуре. называется симметрии фигуры. Говорят также, что фигура обладает симметрией.
плоскости α
плоскости α
Плоскость α
плоскостью
ЗЕРКАЛЬНОЙ
Слайд 24При центральной симметрии относительно точки О (0;0;0)
х1 =
; у1 = ; z1 = .
А(0;1;2) —> А1( )
В(3;-1;4) —> В1( )
С(1;0;-2) —> С1( )
А(0;1;2) —> А1( )
В(3;-1;4) —> В1( )
С(1;0;-2) —> С1( )
Слайд 25
При осевой симметрии относительно оси Ох:
х1 = ; у1
= ; z1 = .
А(0;1;2) —> А1( )
В(3;-1;4) —> В1( )
С(1;0;-2) —> С1( )
А(0;1;2) —> А1( )
В(3;-1;4) —> В1( )
С(1;0;-2) —> С1( )
Слайд 26
При зеркальной симметрии относительно плоскости zy:
х1 =
; у1 = ; z1 = .
А(0;1;2) —> А1( )
В(3;-1;4) —> В1( )
С(1;0;-2) —> С1( )
А(0;1;2) —> А1( )
В(3;-1;4) —> В1( )
С(1;0;-2) —> С1( )
