- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Симметрия (11 класс)
Содержание
- 1. Презентация по геометрии на тему Симметрия (11 класс)
- 2. Эпиграф: “ГЕОМЕТРИЯ есть познание всего сущего”.
- 3. ПодсолнухиЭти дети солнца имеют сразу две формы
- 4. Слайд 4
- 5. Слайд 5
- 6. Слайд 6
- 7. Модель атома Томсона
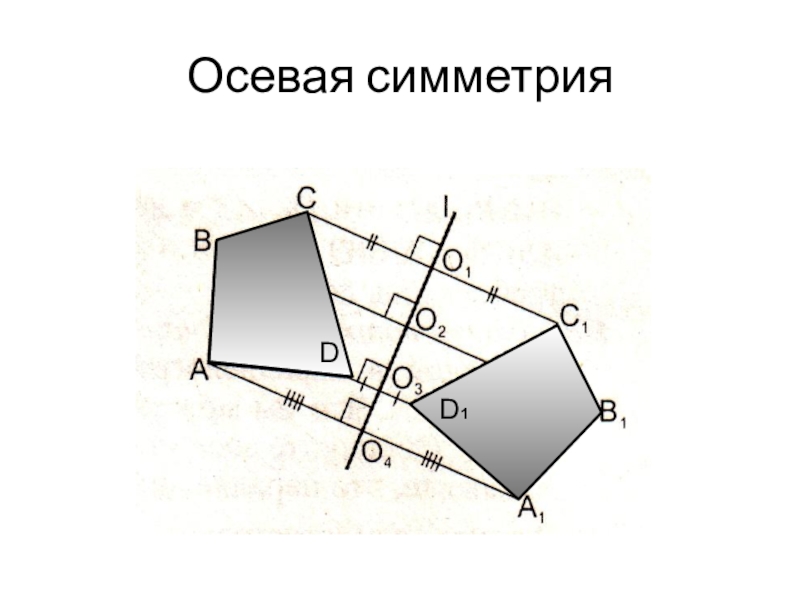
- 8. Осевая симметрия DА1B1C1D1IО1О2О3О4D1DD1
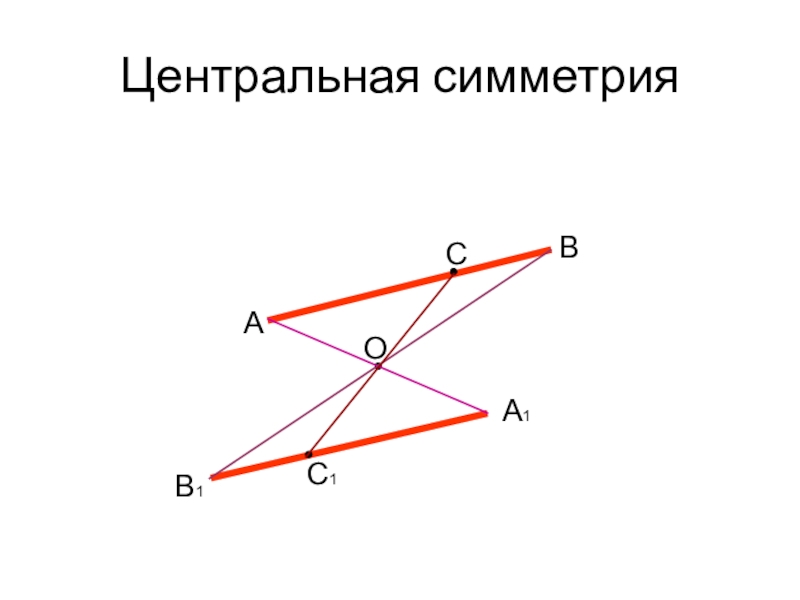
- 9. Центральная симметрияАВСОА1В1С1
- 10. Параллельный переносАВС→аА1В1С1С→а
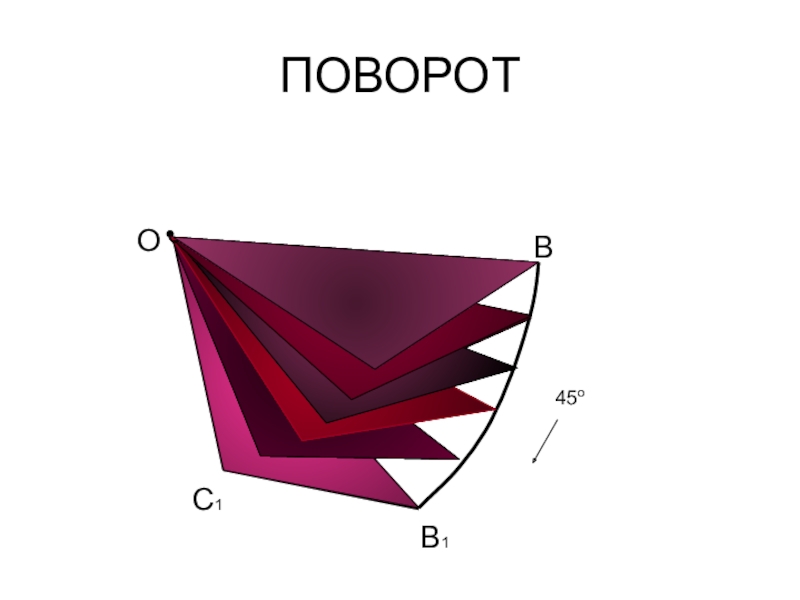
- 11. ПОВОРОТВСВ1С1O
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
- 27. Ряд Фибаначчи
- 28. Слайд 28
- 29. Размеры головы обозначим ГТогда плечи равны
- 30. Слайд 30
- 31. Галактика Млечного пути — поразительный пример зеркальной
- 32. Слайд 32
- 33. Животные, как и люди, симметричны с двух
- 34. Слайд 34
- 35. Вам определенно понадобится микроскоп, чтобы засвидетельствовать красивую
- 36. Слайд 36
- 37. Слайд 37
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. …конца познанью нет!
Эпиграф: “ГЕОМЕТРИЯ есть познание всего сущего”. Платон
Слайд 3
Подсолнухи
Эти дети солнца имеют сразу две формы симметрии – радиальная симметрия,
и числовая симметрия последовательности Фибоначчи. Последовательность Фибоначчи проявляется в числе спиралей из семян цветка.
Слайд 29Размеры головы обозначим Г
Тогда плечи равны
2Г
Размах рук 8Г
Грудь 2Г
Бедро 2Г
Голень 2Г
Пояс – колени 3Г
Пояс – щиколотки 5Г
Макушка – ступня 8Г
Размах одной руки 3Г
Размах рук 8Г
Грудь 2Г
Бедро 2Г
Голень 2Г
Пояс – колени 3Г
Пояс – щиколотки 5Г
Макушка – ступня 8Г
Размах одной руки 3Г
Слайд 31
Галактика Млечного пути — поразительный пример зеркальной симметрии и составлена из
двух главных рукавов, известных как Персей и Щит Центавра. У каждого из этих рукавов есть логарифмическая спираль, подобная оболочке наутилуса, с последовательностью Фибоначчи, которая начинается в центре галактики и расширяется.
Слайд 33Животные, как и люди, симметричны с двух сторон. Это означает, что
есть осевая линия, где они могут быть разделены на две идентичных половины.
Слайд 35Вам определенно понадобится микроскоп, чтобы засвидетельствовать красивую радиальную симметрию в этих
миниатюрных шестисторонних кристаллах. Эта симметрия сформирована в процессе кристаллизации в молекулах воды, которые формируют снежинку. Когда молекулы воды замерзают, они создают водородные связи с гексагональными формами.