- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Сфера (11 класс)
Содержание
- 1. Презентация по геометрии на тему Сфера (11 класс)
- 2. СодержаниеСфера и ее элементыУравнение сферыВзаимное расположение плоскости и сферыПлощадь сферы
- 3. СфераСфера - это фигура, состоящая из всех
- 4. Уравнение сферыM
- 5. Уравнение сферыРасстояние от произвольной точки М(x;y;z) до
- 6. Взаимное расположение плоскости и сферы Пусть d
- 7. Взаимное расположение плоскости и сферы 1) d
- 8. Взаимное расположение плоскости и сферы 3) d>R
- 9. Взаимное расположение плоскости и сферы Касательная плоскость
- 10. Доказательство теоремПредположим, что ОА не перпендикулярен плоскости,
- 11. Площадь сферыДля определения площади сферы воспользуемся понятием
Слайд 2Содержание
Сфера и ее элементы
Уравнение сферы
Взаимное расположение плоскости и сферы
Площадь сферы
Слайд 3Сфера
Сфера - это фигура, состоящая из всех точек пространства, удалённых от
Точка О называется центром сферы,
R-радиус сферы
Любой отрезок, соединяющий центр и какую-нибудь точку сферы, называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы .
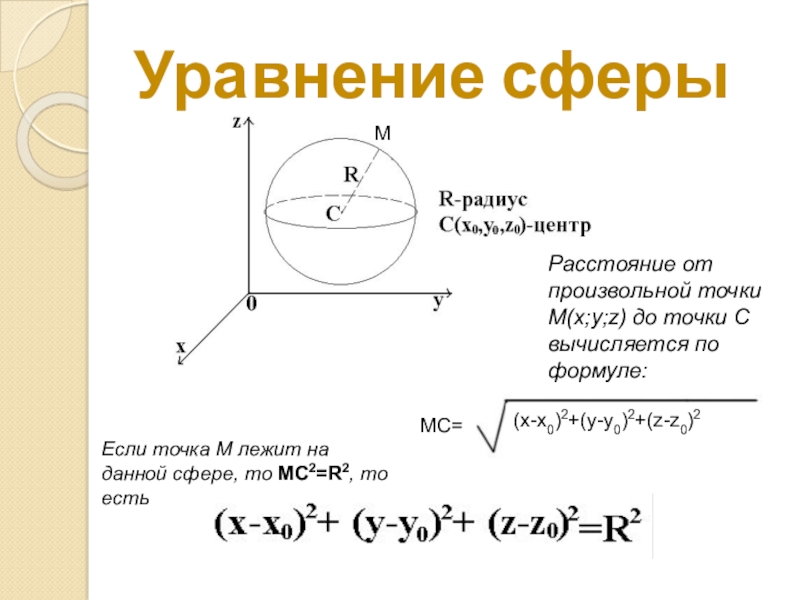
Слайд 5Уравнение сферы
Расстояние от произвольной точки М(x;y;z) до точки С вычисляется по
Если точка М лежит на данной сфере, то МС2=R2, то есть
Слайд 6Взаимное расположение плоскости и сферы
Пусть d - расстояние от центра сферы
Следовательно, C(0;0;d). Поэтому сфера имеет уравнение
Плоскость совпадает с Оxy и поэтому её уравнение имеет вид z=0.
Если точка М(x;y;z) удовлетворяет обоим уравнениям, то она лежит и в плоскости и на сфере, т.е. является общей точкой плоскости и сферы.
Следовательно, возможны 3 решения системы:
Слайд 7Взаимное расположение плоскости и сферы
1) d
уравнение имеет множество решений, сечение сферы плоскостью - окружность с центром в точке
О(0;0;0) и r2=R2 – d2
2) d=R , x2 + y2 =0 , x=y=0 следовательно сфера пересекается с плоскостью только в одной точке О(0;0;0).
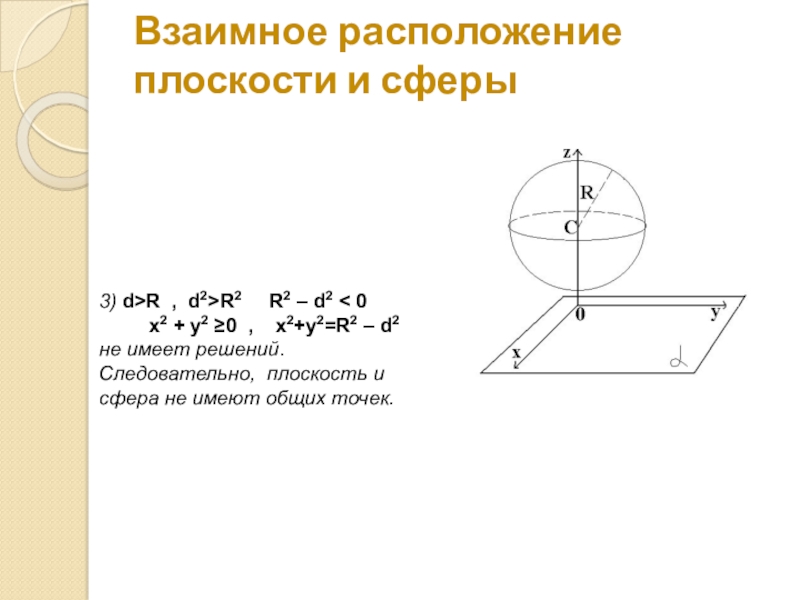
Слайд 8Взаимное расположение плоскости и сферы
3) d>R , d2>R2 R2
x2 + y2 ≥0 , x2+y2=R2 – d2 не имеет решений.
Следовательно, плоскость и сфера не имеют общих точек.
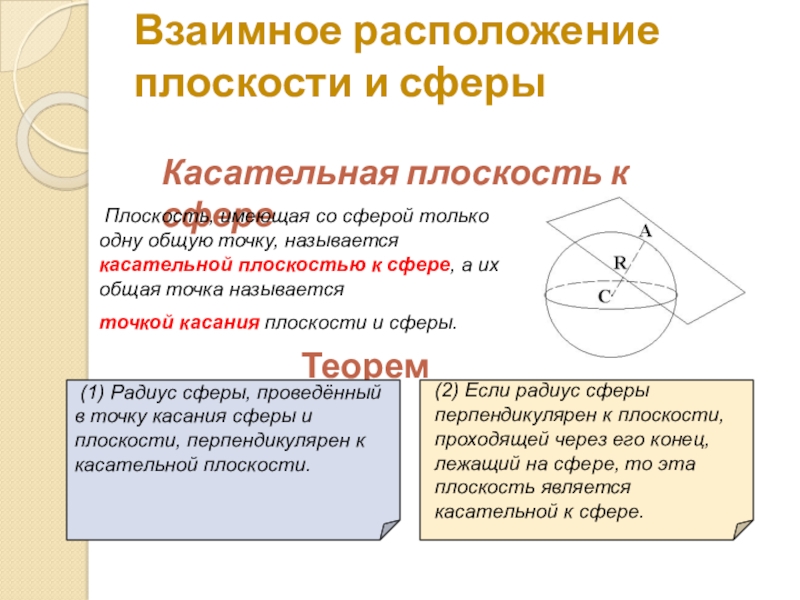
Слайд 9Взаимное расположение плоскости и сферы
Касательная плоскость к сфере
Плоскость, имеющая
точкой касания плоскости и сферы.
Теоремы
(1) Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
(2) Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
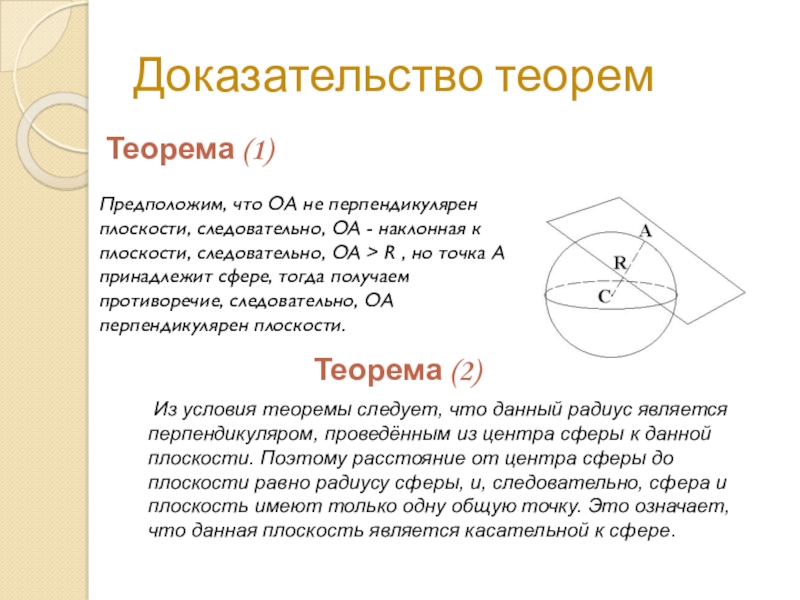
Слайд 10Доказательство теорем
Предположим, что ОА не перпендикулярен плоскости, следовательно, ОА - наклонная
Теорема (1)
Теорема (2)
Из условия теоремы следует, что данный радиус является перпендикуляром, проведённым из центра сферы к данной плоскости. Поэтому расстояние от центра сферы до плоскости равно радиусу сферы, и, следовательно, сфера и плоскость имеют только одну общую точку. Это означает, что данная плоскость является касательной к сфере.
Слайд 11Площадь сферы
Для определения площади сферы воспользуемся понятием описанного многогранника. Многогранник называется
Пусть описанный около сферы многогранник имеет n-граней. Будем неограниченно увеличивать n таким образом, чтобы наибольший размер каждой грани стремился к нулю. За площадь сферы примем предел последовательности площадей поверхностей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани.
Можно доказать, что этот предел существует, и получить формулу для вычисления площади сферы радиуса R :