Сфера и шар. Уравнение сферы
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Сфера и шар. Уравнение сферы (11 класс)
Содержание
- 1. Презентация по геометрии на тему Сфера и шар. Уравнение сферы (11 класс)
- 2. Сферой называется поверхность, состоящая из всех точек
- 3. Сфера как тело вращенияСфера получена вращением полуокружности
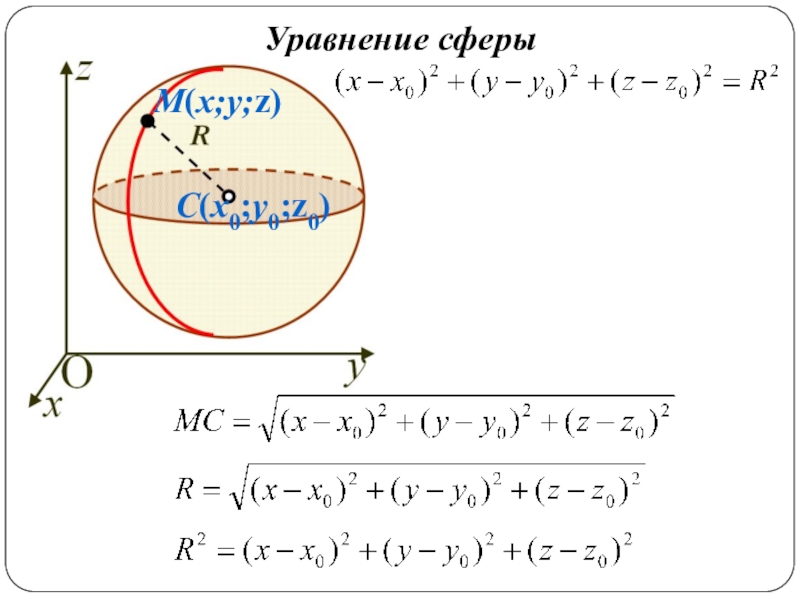
- 4. Уравнение сферыM(x;y;z)С(x0;y0;z0)
- 5. Уравнение сферы№ 576 а, б А(5;
- 6. Уравнение сферы№ 579Докажите, что каждое из следующих
- 7. ЕГЭ задача 8 профильПрямоугольный параллелепипед описан около сферы радиуса 1. Найдите площадь его поверхности.
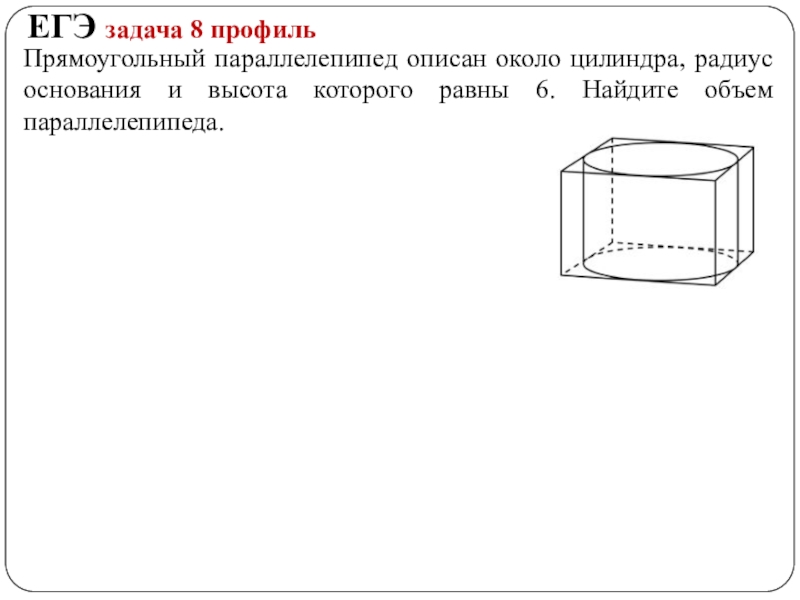
- 8. Прямоугольный параллелепипед описан около цилиндра, радиус основания
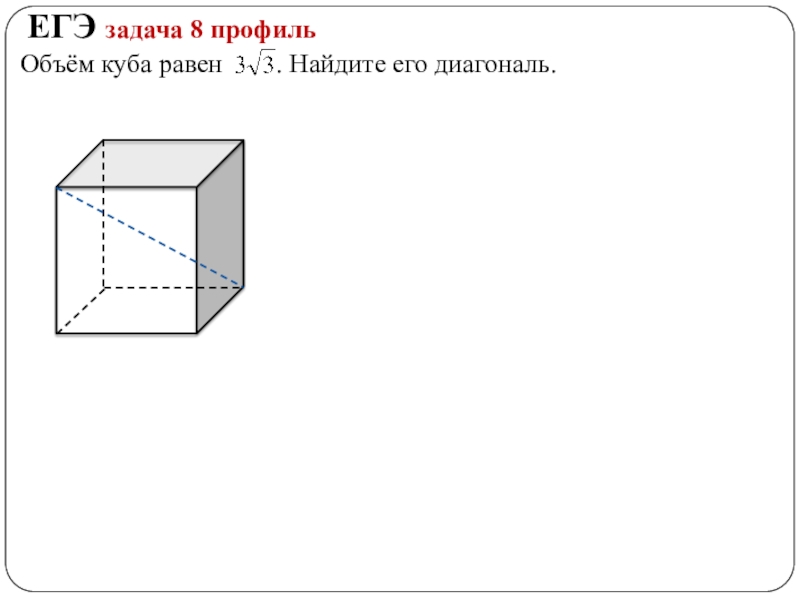
- 9. ЕГЭ задача 8 профильОбъём куба равен . Найдите его диагональ.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.Данная точка называется центром сферы.Данное расстояние называется радиусом сферы.RОтрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы.2R
Слайд 1Домашняя работа:
п. 64, 65 с. 140 -141,
№ 576 в),
№ 577 в), № 579 (в, г) c. 150
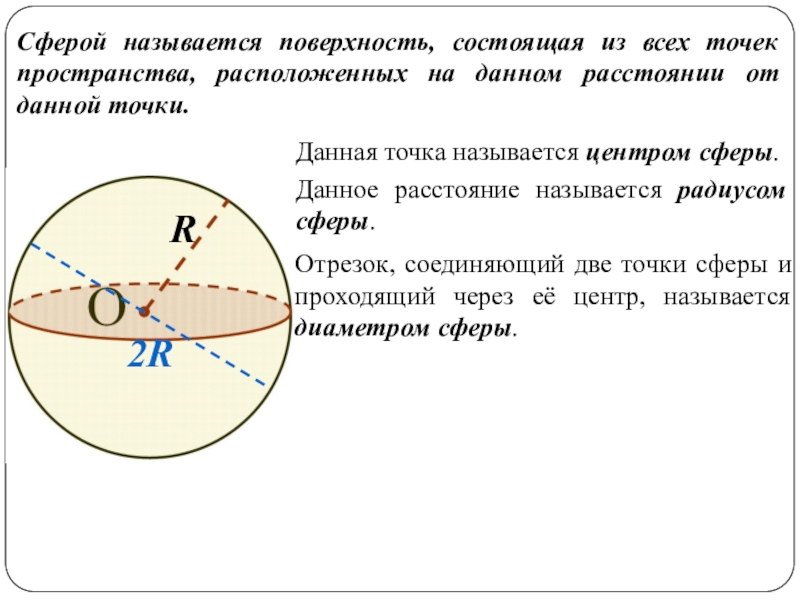
Слайд 2Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном
расстоянии от данной точки.
Данная точка называется центром сферы.
Данное расстояние называется радиусом сферы.
R
Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы.
2R
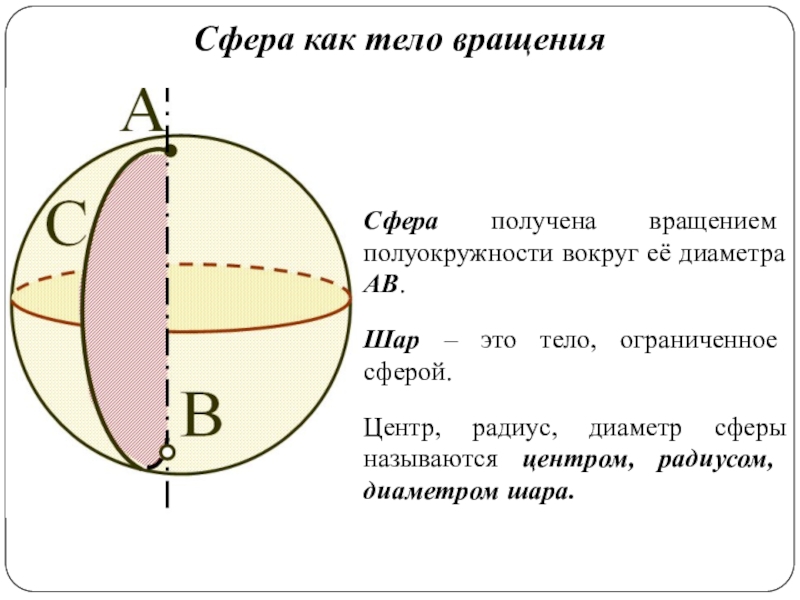
Слайд 3Сфера как тело вращения
Сфера получена вращением полуокружности вокруг её диаметра АВ.
Шар
– это тело, ограниченное сферой.
Центр, радиус, диаметр сферы называются центром, радиусом, диаметром шара.
Слайд 5Уравнение сферы
№ 576 а, б
А(5; 6; 1), R =
5
А(0; 12; 5), R = 1,2
№ 577 а, б
Напишите уравнение сферы с центром в точке А, проходящей через точку N, если: а) А( 2; 2; 0), N(5; 0; 1); б) А( 2; 2; 0), N(0; 0; 0)
№ 578
Найдите координаты центра и радиус сферы, заданной уравнением: а) x2 + y2 + z2 = 49, б) (x – 3)2 + (y + 2)2 + z2 = 2
Напишите уравнение сферы радиуса R с центром в точке А, если:
Слайд 6Уравнение сферы
№ 579
Докажите, что каждое из следующих уравнений является уравнением сферы.
Найдите координаты центра и радиус этой сферы: а) x2 – 4х + y2 + z2 = 0, б) x2 + y2 + z2 – 2у = 24
Слайд 7ЕГЭ задача 8 профиль
Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите
площадь его поверхности.
Слайд 8Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны
6. Найдите объем параллелепипеда.
ЕГЭ задача 8 профиль
