г. Донецка» Панченко И. С.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Решение задач на нахождение площадей параллелограмма и треугольника. Площадь трапеции.
Содержание
- 1. Презентация по геометрии на тему Решение задач на нахождение площадей параллелограмма и треугольника. Площадь трапеции.
- 2. Цель урока: Создать
- 3. Развивающие: - способствовать развитию мыслительной операции
- 4. Тип урока: урок закрепления знаний, умений и
- 5. Основные этапы урока: 1. Организационный момент
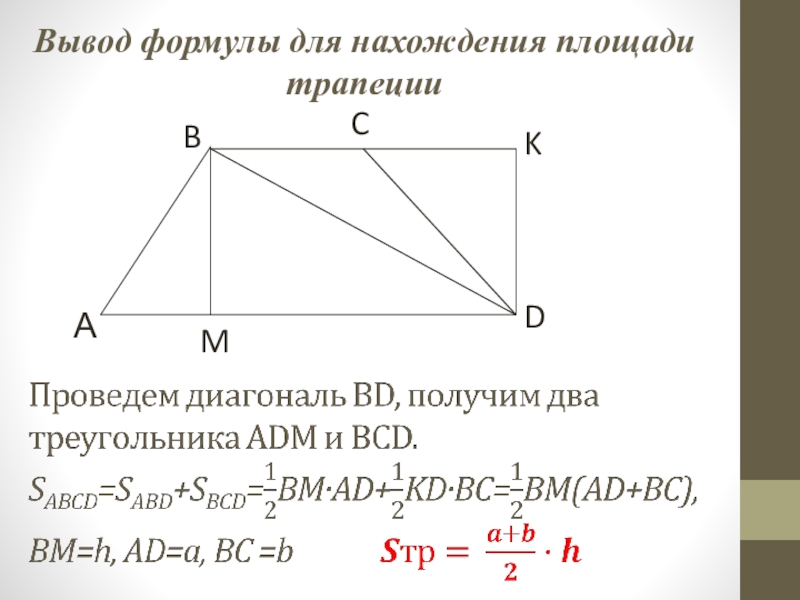
- 6. 8. Вывод формулы для нахождения площади трапеции
- 7. Решение задач на вычисление площадей параллелограмма, треугольника. Площадь трапеции.
- 8. Проверка домашнего задания
- 9. Актуализация знаний
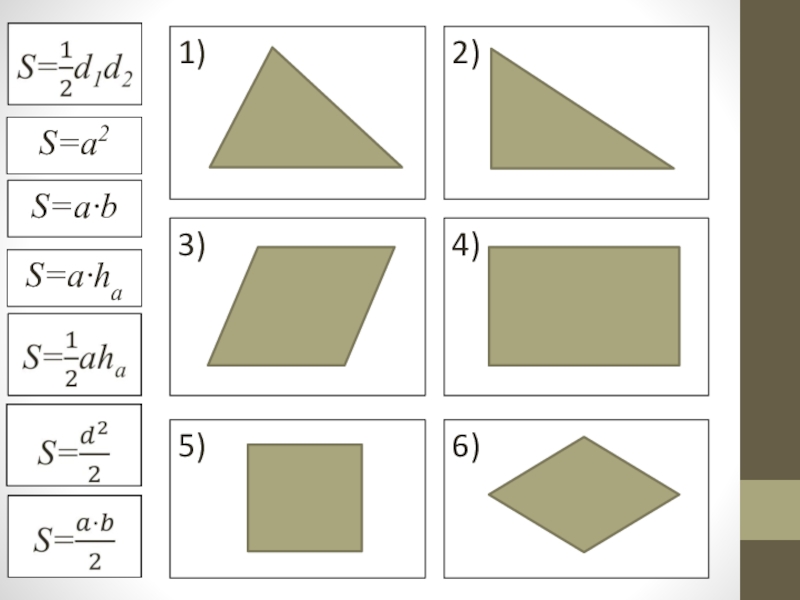
- 10. Повторить формулы нахождения площадей квадрата, прямоугольника, параллелограмма,
- 11. S=a2S=a·bS=a·ha
- 12. Математический диктант. 1. Площадь квадрата
- 13. 5. Параллелограмм, у которого все стороны равны
- 14. Проверим себя: 1. Площадь квадрата со
- 15. 5. Параллелограмм, у которого все стороны
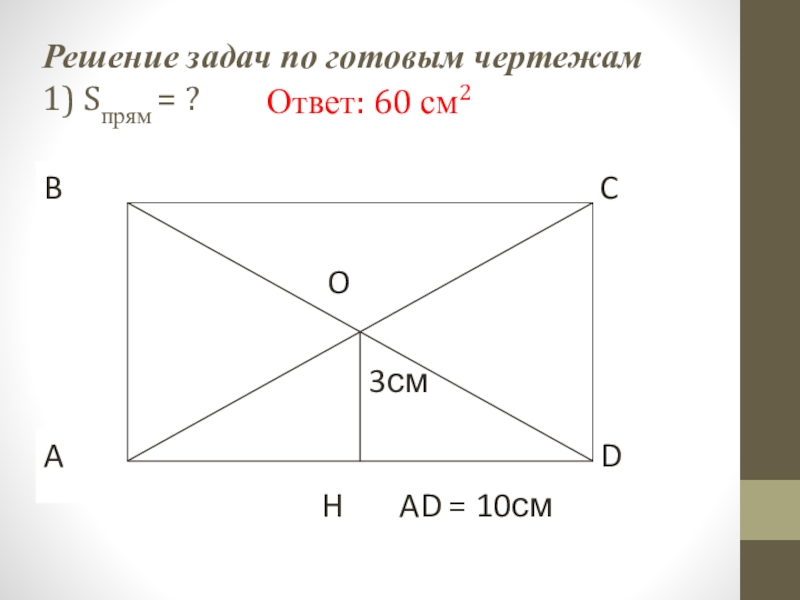
- 16. Решение задач по готовым чертежам 1) Sпрям = ? Ответ: 60 см2
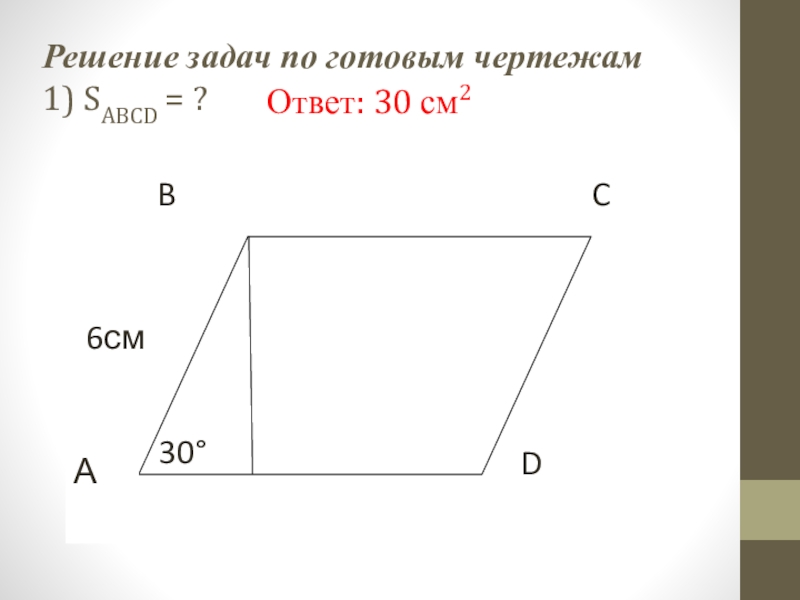
- 17. Решение задач по готовым чертежам 1) SABCD = ? Ответ: 30 см2
- 18. Решение задач по готовым чертежам 1) SABCD = ? Ответ: 20 см2
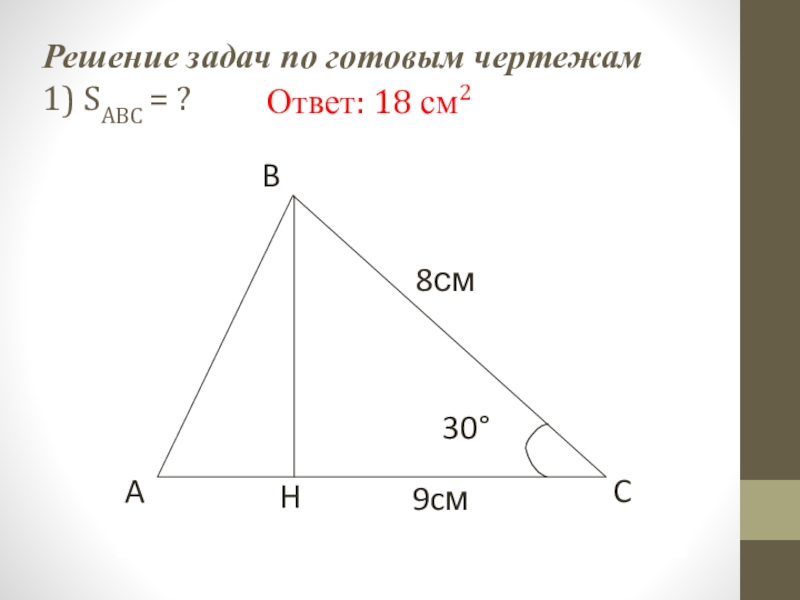
- 19. Решение задач по готовым чертежам 1) SABC = ? Ответ: 18 см2
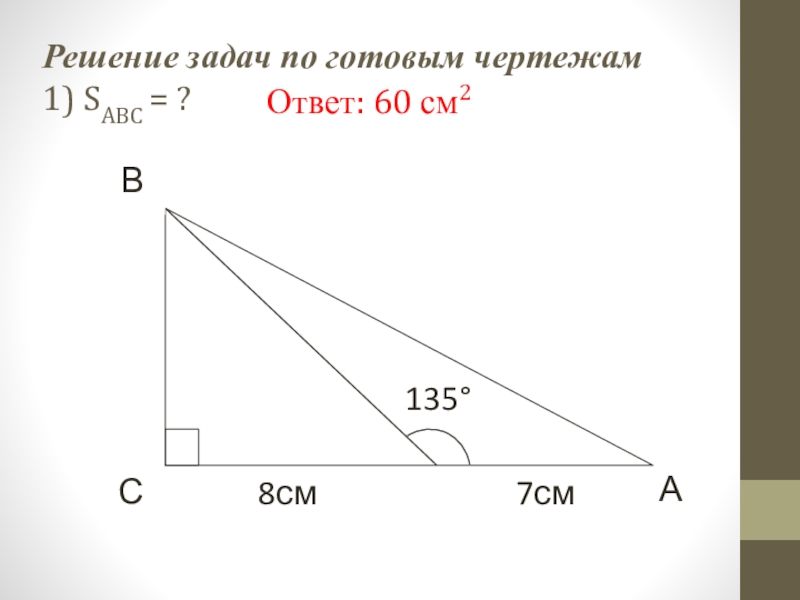
- 20. Решение задач по готовым чертежам 1) SABC = ? Ответ: 60 см2
- 21. Решение задач. Решить на доске и в
- 22. Решение задач. Решить на доске и в
- 23. Физкультминутка
- 24. У прямоугольника хотя бы один угол
- 25. Площадь прямоугольного треугольника равна произведению катетов? Руки,
- 26. Вывод формулы для нахождения площади трапеции
- 27. Закрепление новых знаний учащихся «Аквариум». Класс делится
- 28. Задача 1. Основания трапеции и высота относятся
- 29. Задача 4. Площадь трапеции 72 см2, а
- 30. Исторические сведения
- 31. Вычисление площадей в древности.
- 32. Узкая полоса земли между Нилом и пустыней
- 33. Евклид – древнегреческий ученый, живший в
- 34. Архимед – древнегреческий ученый, математик и
- 35. В своем произведении «Об измерении круга», Архимед
- 36. Одним из поздних греческих математиков был Герон
- 37. В своем наиболее важном произведении «Метрика» Герон
- 38. Пишем самостоятельную работу
- 39. Проверим ответы Самостоятельная работа. Решение тестовых заданий.
- 40. 3. В треугольнике высота, опущенная к стороне с
- 41. Проверим ответы Самостоятельная работа. Решение тестовых заданий.
- 42. 3. В треугольнике высота, опущенная к стороне с
- 43. Подведение итогов урока. Рефлексия. Чему
- 44. Домашнее задание. Повторить формулы для
- 45. Слайд 45
Цель урока: Создать условия для развития умений вычислять площади фигур, применяя изученные свойства и формулы. Обучающие: - закрепить навыки вычисление площадей фигур по формулам; - способствовать формированию умений применять изученные свойства
Слайд 2 Цель урока: Создать условия для развития умений вычислять площади фигур, применяя
изученные свойства и формулы.
Обучающие:
- закрепить навыки вычисление площадей фигур по формулам;
- способствовать формированию умений применять изученные свойства и формулы в типовой и нестандартной ситуациях.
Слайд 3Развивающие: - способствовать развитию мыслительной операции анализа, сравнения, обобщения; - способствовать развитию
коммуникативных качеств личности.
Воспитательные:
- способствовать воспитанию трудолюбия, настойчивости в достижении цели, аккуратности.
Слайд 4Тип урока: урок закрепления знаний, умений и отработки навыков. Форма урока: урок-практикум. Формы
работы: фронтальная, дифференцированная.
Оборудование: презентация; текстовые документы.
Слайд 5Основные этапы урока: 1. Организационный момент –1 минута. 2. Постановка цели урока –3
минуты.
3. Проверка домашнего задания – 5минут.
4. Актуализация опорных знаний:
а) соответствие – 5 минут;
б) математический диктант – 5минут;
5. Работа по готовым чертежам – 10минут.
6. Решение задач – 15минут.
7. Физкультминутка - 1минута.
Слайд 68. Вывод формулы для нахождения площади трапеции – 7 минут. 9. «Аквариум»
– 8минут.
10. Исторические сведения – 7минут.
11. Самостоятельная работа. Решение тестовых заданий – 15минут.
12. Подведение итога урока – 5минут.
13. Рефлексия – 2минуты.
14. Постановка домашнего задания – 1минута.
Слайд 10Повторить формулы нахождения площадей квадрата, прямоугольника, параллелограмма, треугольника. Даны набор формул
геометрических фигур и набор изображений геометрических фигур. В течение 5 минут учащиеся должны для каждой геометрической фигуры найти соответствующую формулу для вычисления ее площади.
Слайд 12 Математический диктант. 1. Площадь квадрата со стороной, равной 1 м, равна … 2.
Равные фигуры имеют …
площади.
3. Стороны параллелограмма, которые выходят из одной вершины называются …
4. Четырехугольник, у которого противолежащие стороны попарно параллельны, называется …
Слайд 135. Параллелограмм, у которого все стороны равны называется … 6. Четырехугольник, у
которого две стороны параллельны, а две другие не параллельны, называется …
7. Если длину прямоугольника умножить на ширину, то получится …
8. Не параллельные стороны трапеции называются …
Слайд 14Проверим себя: 1. Площадь квадрата со стороной, равной 1м, равна 1м2. 2. Равные
фигуры имеют равные площади.
3. Стороны параллелограмма, которые выходят из одной вершины называются соседними.
4. Четырехугольник, у которого противолежащие стороны попарно параллельны, называется параллельными.
Слайд 15 5. Параллелограмм, у которого все стороны равны называется ромбом. 6. Четырехугольник, у
которого две стороны параллельны, а две другие не параллельны, называется трапеция.
7. Если длину прямоугольника умножить на ширину, то получится площадь прямоугольника.
8. Не параллельные стороны трапеции называются боковыми.
Слайд 21Решение задач. Решить на доске и в тетрадях задачи (один работает
у доски, остальные в тетрадях):
1. Стороны прямоугольника относится как 9:1, а их разность равна 32см. Найди: а)площадь прямоугольника; б)сторону квадрата ,площадь которого равна площади прямоугольника.
2. Периметр ромба равен 72см, а один из углов 30°. Найти площадь ромба.
Ответ: а)144см2; б)12см.
Ответ: 162см2.
Слайд 22Решение задач. Решить на доске и в тетрадях задачи (один работает
у доски, остальные в тетрадях):
3. Основание треугольника равно 8см,а высота, проведенная к нему,-3см. Какой должна быть высота второго треугольника с основанием 6см, чтобы его площадь была в 3 раза больше площади первого треугольника?
Ответ: 12см.
Слайд 24
У прямоугольника хотя бы один угол острый?
Голова
У квадрата все стороны
равны?
Да
У параллелограмма все углы равны?
Нет
У ромба диагонали пересекаются под прямым углом?
Да
Нет
Слайд 25Площадь прямоугольного треугольника равна произведению катетов?
Руки, ноги
Площадь прямоугольника равна а
умножить на b?
Да (Хлопаем руками)
Средняя линия трапеции соединяет противолежащие вершины?
Нет (Топаем ногами)
Сумма внутренних углов четырехугольника равна 360° ?
Нет (Топаем ногами)
Да (Хлопаем руками)
Слайд 27Закрепление новых знаний учащихся «Аквариум». Класс делится на группы по 5-6 человек.
Одна из групп выходит к доске. Эта группа сначала зачитывает вслух задание, затем в течение 5 минут обсуждает его, и пытается найти общее решение, остальные группы внимательно слушают обсуждение. После дискуссии класс должен либо принять предложенное решение, либо опровергнуть его. После решения первой задачи место в «аквариуме» занимает следующая группа .
Слайд 28Задача 1. Основания трапеции и высота относятся как 5:6:4. Найти меньшее
основание трапеции, если ее площадь равна 88 см2.
Задача 2. Основания трапеции равны 9 см и 11 см, а ее площадь – 150 см2. Найти высоту трапеции .
Задача 3. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны 6 см, а больший угол равен 135° .
(Ответ: 10 см)
(Ответ: 15 см)
(Ответ: 54 см2)
Слайд 29Задача 4. Площадь трапеции 72 см2, а ее высота – 9
см. Найдите основания трапеции, если одно из них в 3 раза больше второго .
Задача 5. Найдите площадь равнобедренной трапеции, если ее меньшее основание равно 18 см, высота – 9 см, а острый угол равен 45°?
(Ответ: 4 см и 12 см)
(Ответ: 243 см2)
Слайд 31 Вычисление площадей в древности. Зачатки геометрических знаний, связанных с измерением площадей,
теряются в глубине тысячелетий. Еще 4-5 тыс . лет назад вавилоняне умели определять площадь прямоугольника и трапеции в квадратных единицах. 5 000 лет назад древние египтяне умели определять площади.
Слайд 32Узкая полоса земли между Нилом и пустыней была плодородной. С каждой
единицы ее площади люди платили налог. Но ежегодно эта полоска затоплялась Нилом. После спада воды надо было восстанавливать границы. Необходимость быстро и правильно определять площадь была одной из причин раннего развития геометрии как науки об измерении земли.
Слайд 33 Евклид – древнегреческий ученый, живший в III нашей эры. В своих
«Началах» Евклид не употребляет слово «площадь», так как он под самим словом «фигура» понимает часть плоскости, ограниченной замкнутой линией. Евклид не выражает результат измерения площади числом, а сравнивает площади разных фигур между собой. Как и другие ученые древности, Евклид занимается вопросами превращения одних фигур в другие, им равновеликие. При этом Евклид оперирует самими площадями, а не числами, которые выражают эти площади.
Слайд 34 Архимед – древнегреческий ученый, математик и механик. Развил метод нахождения площадей
поверхностей и объемов различных фигур и тел. Архимед вычислил площади эллипса, сегмента, а так же различных тел вращения. Архимеду принадлежит формула для определения площади треугольника через три его стороны, которую мы называем формулой Герона.
Слайд 35В своем произведении «Об измерении круга», Архимед на основе строгих теоретических
рассуждений вычислил отношение длины окружности к своему диаметру и нашел приближенное значение числа π, которое называется числом Архимеда.
Слайд 36Одним из поздних греческих математиков был Герон Александрийский. О жизни Герона
дошли лишь обрывочные сведения. Известно, что он был выдающимся ученым-механиком. Он много внимания уделял практическому применению геометрии. Одна из книг Герона «Геометрика» является сборником формул и соответствующих задач. Она содержит примеры на вычисление площадей квадратов, прямоугольников, треугольников, круга, а так же сегмента и сектора круга.
Слайд 37В своем наиболее важном произведении «Метрика» Герон излагает доказательство формулы для
площади треугольника, которую мы называем формулой Герона. Практические правила Герона для вычисления площадей применялись греческими, римскими и средневековыми землемерами и техниками.
Слайд 39 Проверим ответы Самостоятельная работа. Решение тестовых заданий. Вариант 1. 1. Площадь прямоугольника 20 см2,
одна из сторон – 5 см. Найти другую сторону.
1) 15см 2) 4 см 3) 5 см 4) 100 см
2. В параллелограмме одна из сторон 7 см, высота, опущенная на нее 3 см. Найти площадь.
1) 21см 2) 10 см2 3) 21 см2 4) 10,5 см2
Слайд 403. В треугольнике высота, опущенная к стороне с длинной 10 см, равна
6 см. Найти площадь.
1) 60см2 2) 30 см2 3) 16 см2 4) 8 см2
4. Основания трапеции 5 и 8 см, а высота 12 см. Найти площадь.
1) 13см2 2) 156 см2 3) 78 см2 4) 39 см2
5. Площадь квадрата 4 м2. Найти периметр квадрата.
1) 1 м 2) 8 м 3) 2 м 4) 16 м
Отметка: «5» - нет ошибок, «4» - 1 ошибка, «3» - 2 ошибки, более двух неверных ответов – выучи формулу, упражняйся в устном счете.
Слайд 41 Проверим ответы Самостоятельная работа. Решение тестовых заданий. Вариант 2. 1. Площадь прямоугольника 40 см2, одна
из сторон – 10 см. Найти другую сторону.
1) 4 см 2) 2 см 3) 30 см 4) 200 см
2. В параллелограмме одна из сторон 8 см, высота, опущенная на нее 5 см. Найти площадь.
1) 13см 2) 40 см2 3) 40 см 4) 26 см2
Слайд 423. В треугольнике высота, опущенная к стороне с длинной 9 см, равна
4 см. Найти площадь.
1) 35 см2 2) 13 см2 3) 18 см2 4) 72 см2
4. Основания трапеции 4 и 9 см, а высота 6 см. Найти площадь.
1) 13см2 2) 3 см2 3) 39 см2 4) 78 см2
5. Площадь квадрата 16 м2. Найти периметр квадрата.
1) 4 м 2) 64 м 3) 8 м 4) 16 м
Отметка: «5» - нет ошибок, «4» - 1 ошибка, «3» - 2 ошибки, более двух неверных ответов – выучи формулу, упражняйся в устном счете.
Слайд 43 Подведение итогов урока. Рефлексия. Чему вы научились при изучении темы раздела; Какими
навыками, умениями овладели;
Какими формулами, понятиями воспользовались при решении задач?
Решение каких задач показалось вам сложным?
Какие вопросы требуют вашего особого внимания?
Какие задачи вам понравилось решать?
Слайд 44 Домашнее задание. Повторить формулы для вычисления площади прямоугольника, квадрата, параллелограмма, ромба,
треугольника, трапеции;
№ 471(б), 477, 482 (учебник).
