- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Решение задач (10-11 класс)
Содержание
- 1. Презентация по геометрии на тему Решение задач (10-11 класс)
- 2. Объем прямоугольного параллелепипеда4. Составьте план вычисления длины отрезка AD и объема параллелепипедаСАDВa????
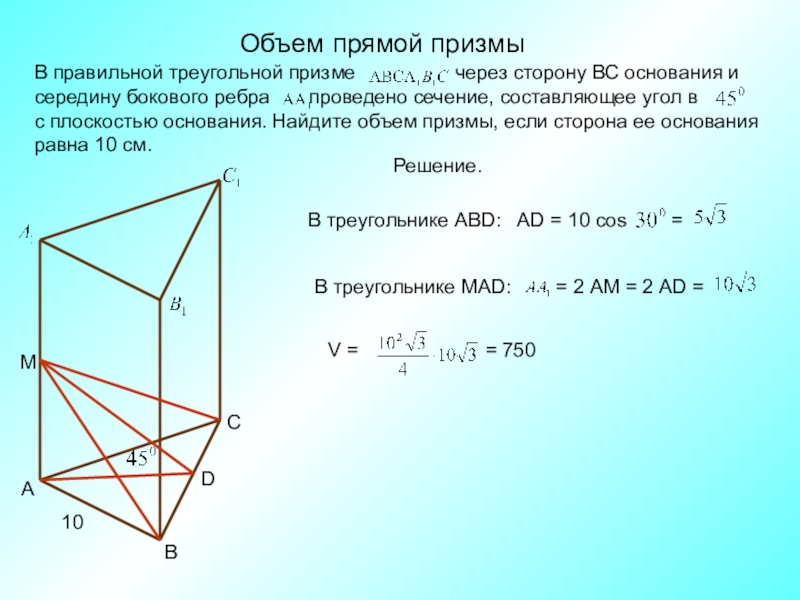
- 3. Объем прямой призмыСВАМD10Решение.
- 4. Объем призмы и цилиндраДана правильная шестиугольная призма,
- 5. Задача Дано: АМ – наклонная к плоскости
- 6. Задача Дано: луч АМ образует равные острые
- 7. Объем наклонной призмыНайдите объем параллелепипеда.САDВКαаРешение. тогда cos 60 = cos α ∙ cos 30,
- 8. Если боковые ребра пирамиды равны (или составляют
- 9. Если двугранные углы при основании пирамиды равны
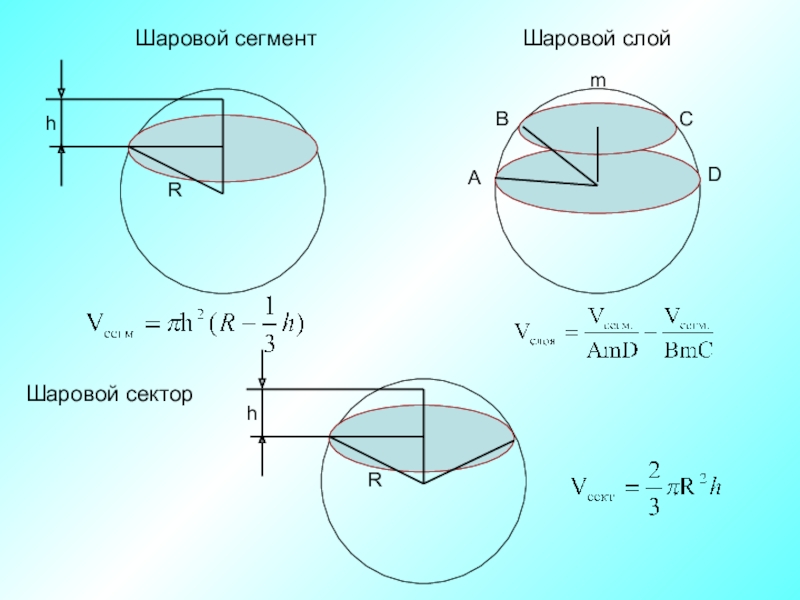
- 10. Шаровой сегментШаровой слойШаровой сектор
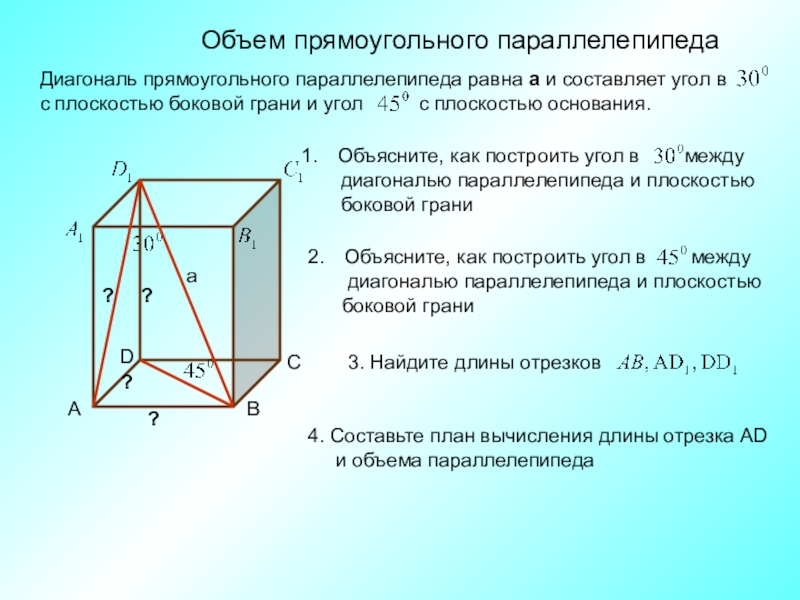
Слайд 2Объем прямоугольного параллелепипеда
4. Составьте план вычисления длины отрезка AD
С
А
D
В
a
?
?
?
?
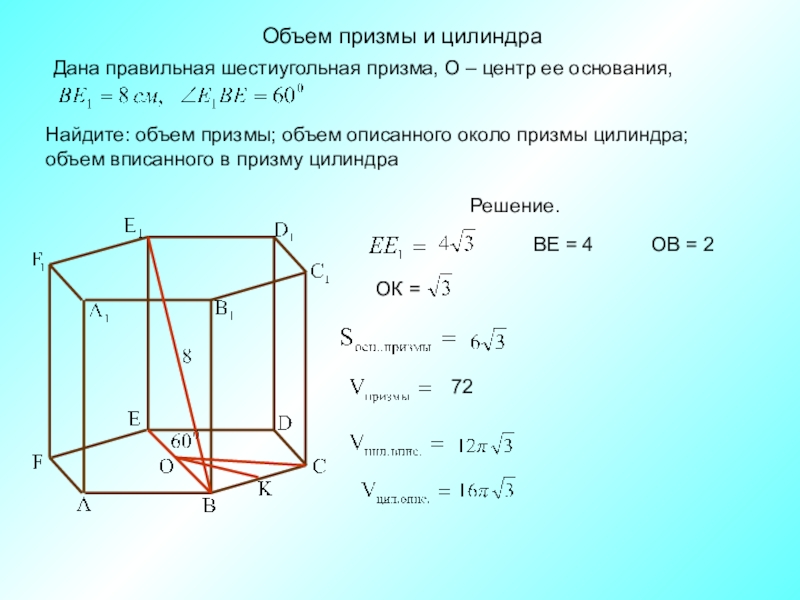
Слайд 4Объем призмы и цилиндра
Дана правильная шестиугольная призма, О – центр ее
Найдите: объем призмы; объем описанного около призмы цилиндра;
объем вписанного в призму цилиндра
Решение.
ВЕ = 4
ОВ = 2
ОК =
72
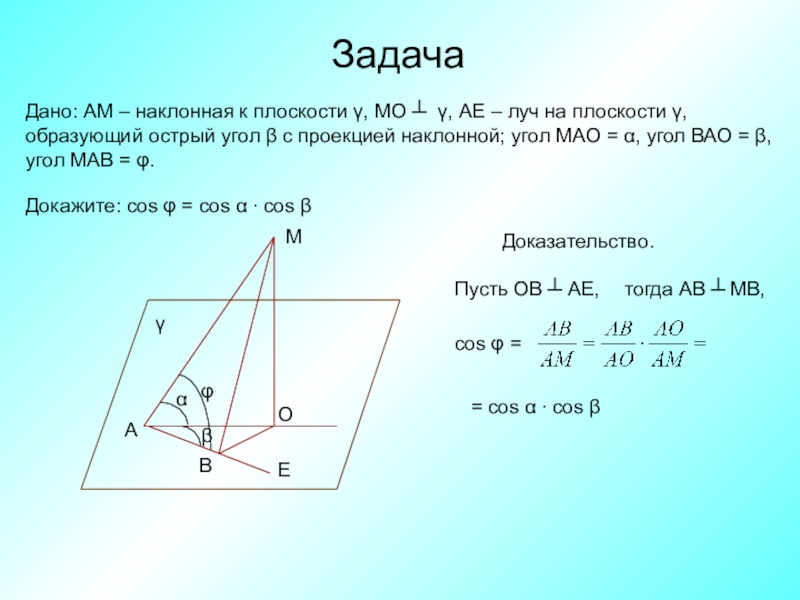
Слайд 5Задача
Дано: АМ – наклонная к плоскости γ, МО ┴ γ,
образующий острый угол β с проекцией наклонной; угол МАО = α, угол ВАО = β,
угол МАВ = φ.
Докажите: cos φ = cos α ∙ cos β
β
α
Е
В
О
А
М
φ
γ
Доказательство.
Пусть ОВ ┴ АЕ,
тогда АВ ┴ МВ,
cos φ =
= cos α ∙ cos β
Слайд 6Задача
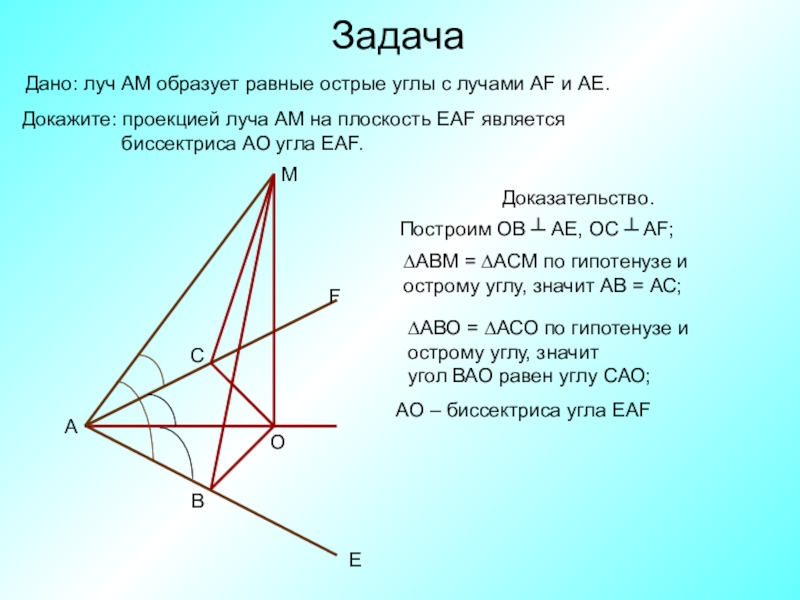
Дано: луч АМ образует равные острые углы с лучами AF
Докажите: проекцией луча АМ на плоскость EAF является
биссектриса АО угла EAF.
C
B
O
F
Е
М
А
Доказательство.
Построим ОВ ┴ АЕ, ОС ┴ АF;
∆АВМ = ∆АСМ по гипотенузе и острому углу, значит АВ = АС;
∆АВО = ∆АСО по гипотенузе и
острому углу, значит
угол ВАО равен углу САО;
АО – биссектриса угла EAF
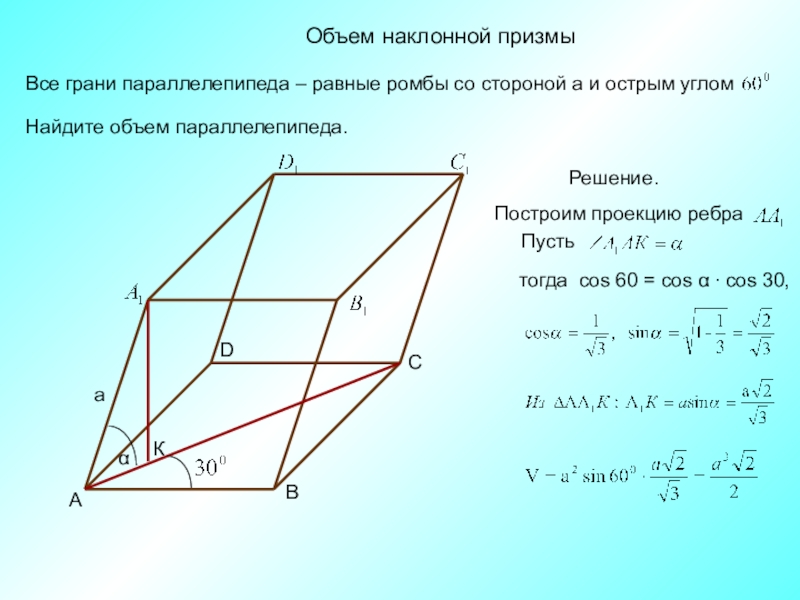
Слайд 7Объем наклонной призмы
Найдите объем параллелепипеда.
С
А
D
В
К
α
а
Решение.
тогда cos 60 = cos α
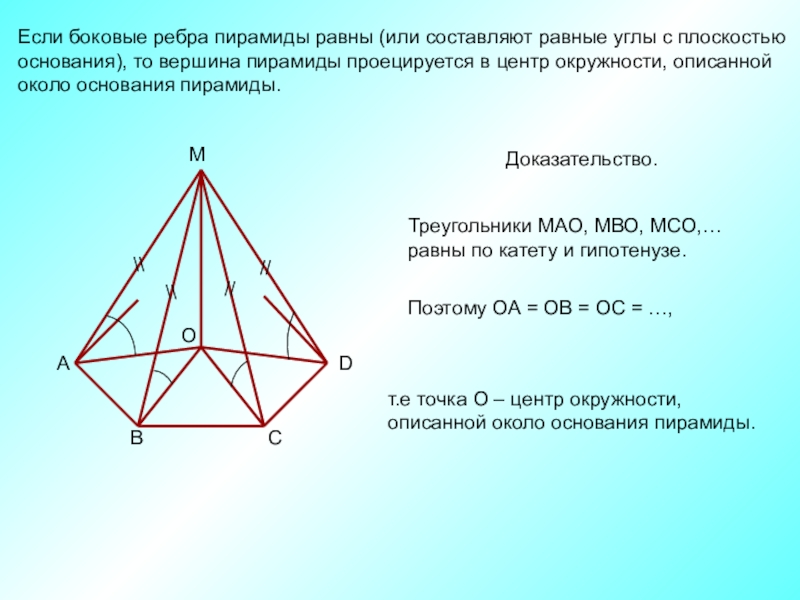
Слайд 8Если боковые ребра пирамиды равны (или составляют равные углы с плоскостью
основания), то вершина пирамиды проецируется в центр окружности, описанной
около основания пирамиды.
Доказательство.
Треугольники МАО, МВО, МСО,…
равны по катету и гипотенузе.
Поэтому ОА = ОВ = ОС = …,
т.е точка О – центр окружности,
описанной около основания пирамиды.
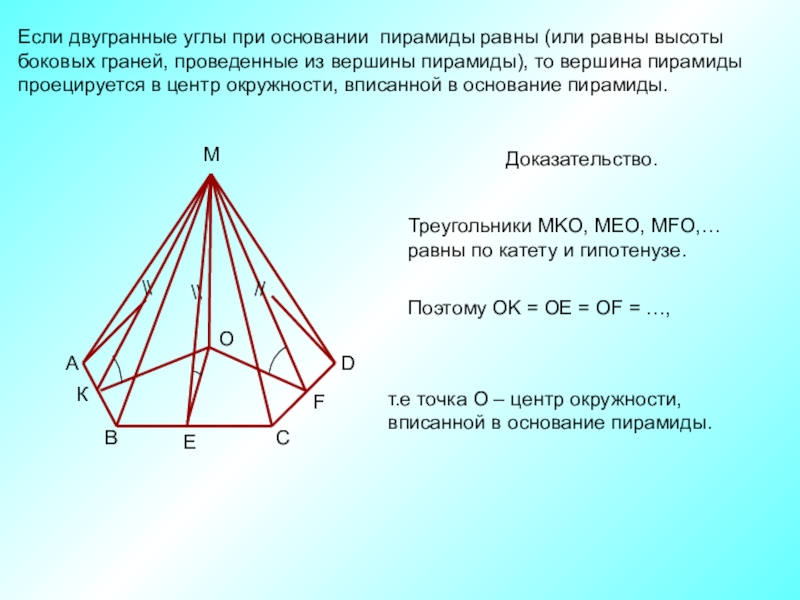
Слайд 9Если двугранные углы при основании пирамиды равны (или равны высоты
боковых
проецируется в центр окружности, вписанной в основание пирамиды.
Доказательство.
Треугольники МKО, МEО, МFО,…
равны по катету и гипотенузе.
Поэтому ОK = ОE = ОF = …,
т.е точка О – центр окружности,
вписанной в основание пирамиды.