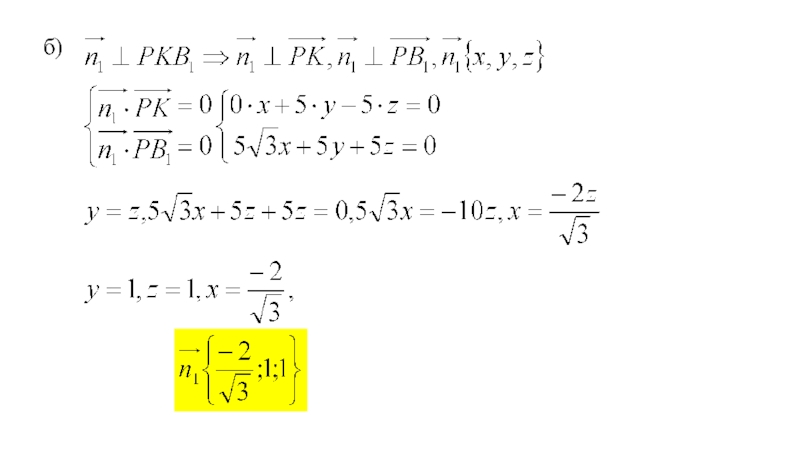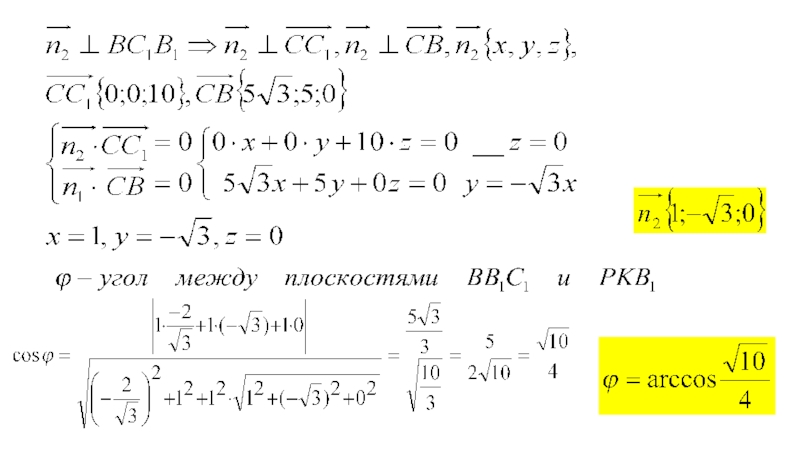- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Решение стереометрических задач
Содержание
- 1. Презентация по геометрии на тему Решение стереометрических задач
- 2. Основные виды задачНахождение угламежду прямыми;между прямой и
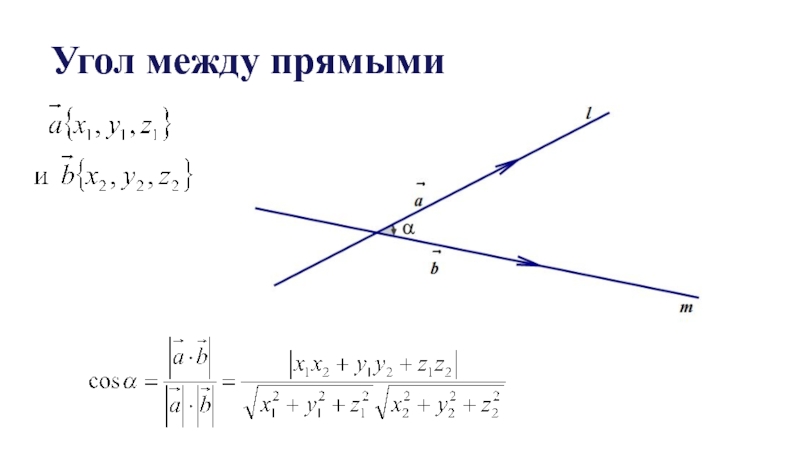
- 3. Угол между прямыми
- 4. №1. В кубе ABCDA1B1C1D1 найдите угол между
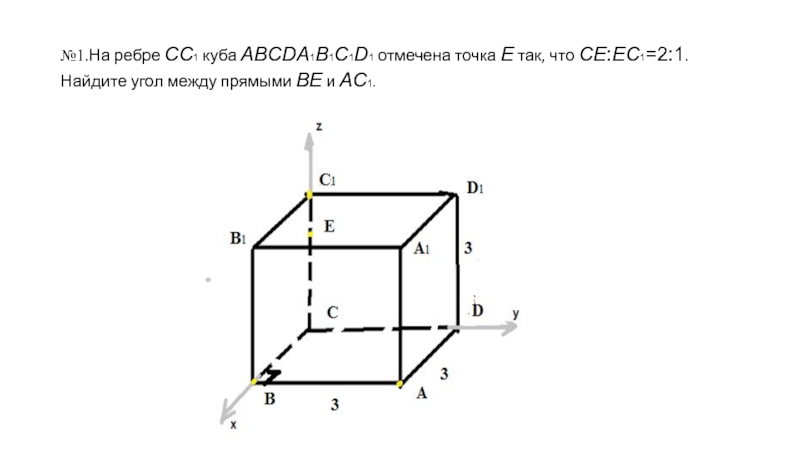
- 5. №1.На ребре CC1 куба ABCDA1B1C1D1 отмечена точка E так, что CE:EC1=2:1. Найдите угол между прямыми BE и AC1.
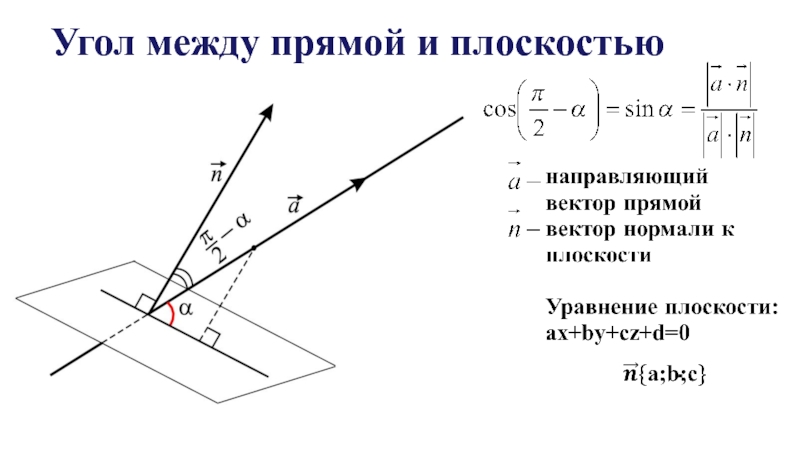
- 6. Угол между прямой и плоскостью
- 7. Координаты вектора нормали к плоскостиA(x;y;z) : аx+by+сz+d=0B(x1;y1;z1) : аx1+by1+сz1+d=0 C(x2;y2;z2) : аx2+by2+сz2+d=0
- 8. Координаты вектора нормали к плоскости
- 9. №2. В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите угол
- 10. Ответ:Пусть α – угол между ВС1 и плоскостью BA1C
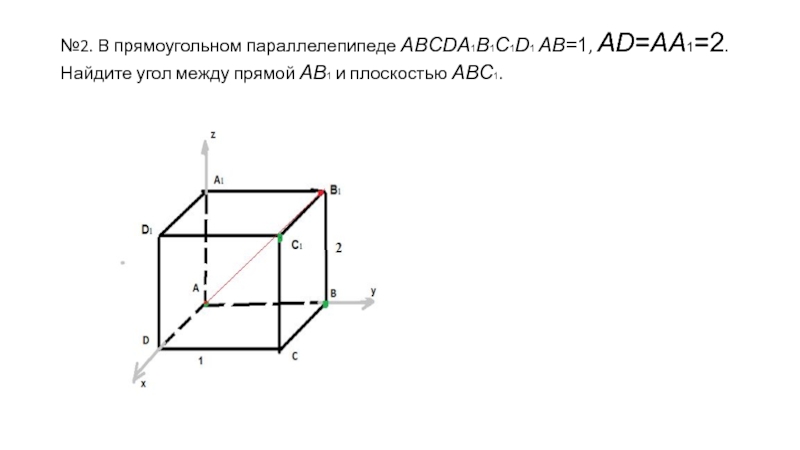
- 11. №2. В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=1, AD=AA1=2. Найдите угол между прямой AB1 и плоскостью ABC1.
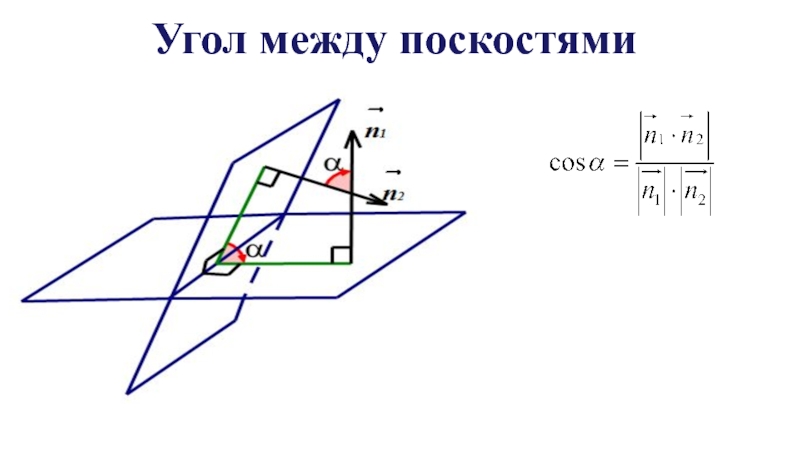
- 12. Угол между поскостями
- 13. №3. В правильной треугольной призме ABCA1B1C1 стороны
- 14. Слайд 14
- 15. №3. В правильной четырёхугольной призме ABCDA1 В1
- 16. №4. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1
- 17. Слайд 17
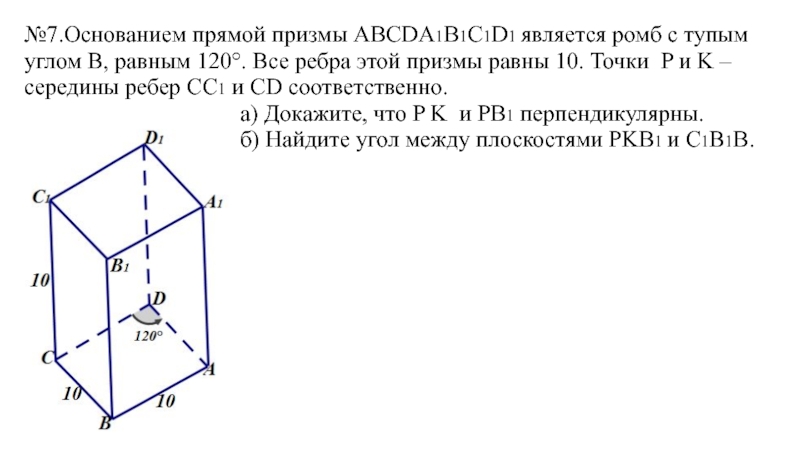
- 18. №7.Основанием прямой призмы ABCDA1B1C1D1 является ромб с
- 19. а)
- 20. б)
- 21. Слайд 21
- 22. Слайд 22
Основные виды задачНахождение угламежду прямыми;между прямой и плоскостью;между плоскостями;Нахождение расстоянияот точки до прямой;от точки до плоскости;между двумя скрещивающимися прямыми.
Слайд 2Основные виды задач
Нахождение угла
между прямыми;
между прямой и плоскостью;
между плоскостями;
Нахождение расстояния
от точки
до прямой;
от точки до плоскости;
между двумя скрещивающимися прямыми.
от точки до плоскости;
между двумя скрещивающимися прямыми.
Слайд 4№1. В кубе ABCDA1B1C1D1 найдите угол между прямыми A1АCА1 и DE,
если E - середина ребра СС11
.
Слайд 5№1.На ребре CC1 куба ABCDA1B1C1D1 отмечена точка E так, что CE:EC1=2:1. Найдите угол между
прямыми BE и AC1.
Слайд 7Координаты вектора нормали к плоскости
A(x;y;z) : аx+by+сz+d=0
B(x1;y1;z1) : аx1+by1+сz1+d=0
C(x2;y2;z2) : аx2+by2+сz2+d=0
Слайд 9№2. В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите угол между плоскостью A1BC и
прямой BC1, если AA1 = 8, AB = 6, BC = 15.
Уравнение плоскости: ax+by+cz+d=0 (1)
B(0;0;0): а0+b0+с0+d=0, d=0
A1(6;0;8):6а+ b0+8с+0=0 , 6a+8c=0
C(0;15;0): 0а+15b+0с+0=0, 15b=0, b=0
BA1C:
6a+8c=0
Слайд 11№2. В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=1, AD=AA1=2. Найдите угол между прямой AB1 и
плоскостью ABC1.
Слайд 13№3. В правильной треугольной призме ABCA1B1C1 стороны основания равны 2, боковые
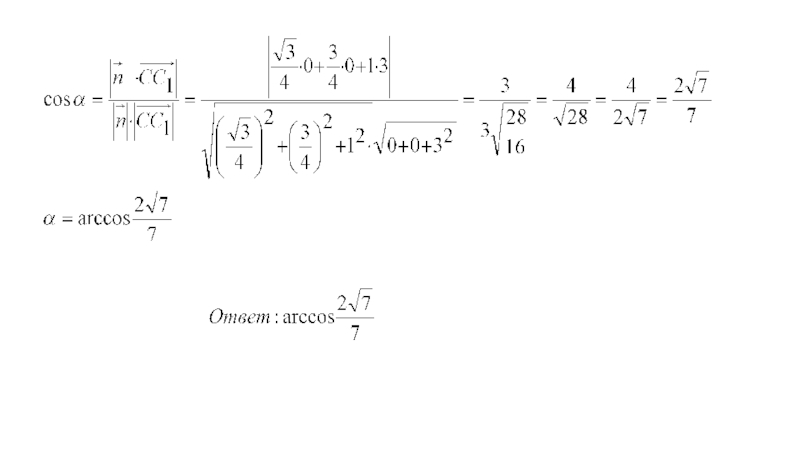
рёбра равны 3, точка D -середина ребра CC1. Найдите угол между плоскостями ABC и ADB1.
.
Решение. Oxyz
Проведем AK
CB, CK=KB=1
AKC ,
K=90 , AK=
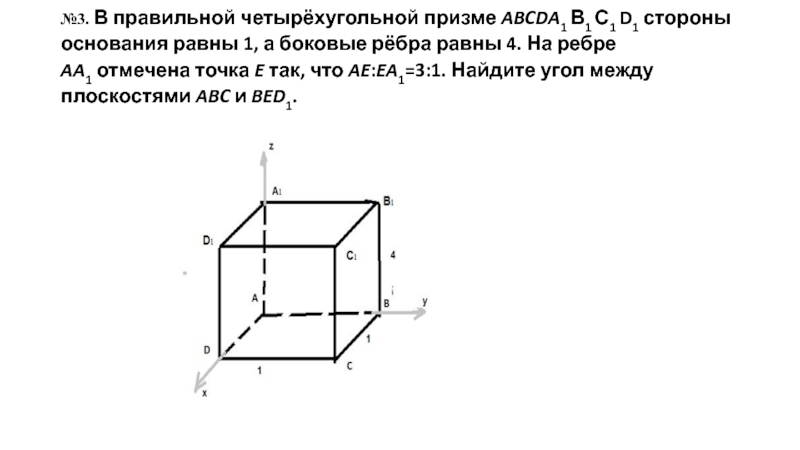
Слайд 15№3. В правильной четырёхугольной призме ABCDA1 В1 С1 D1 стороны основания равны
1, а боковые рёбра равны 4. На ребре AA1 отмечена точка E так, что AE:EA1=3:1. Найдите угол между плоскостями ABC и BED1.
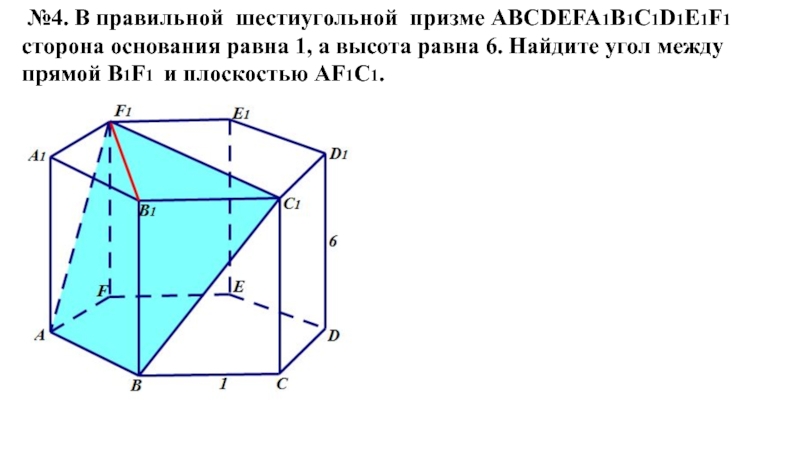
Слайд 16 №4. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона основания равна 1,
а высота равна 6. Найдите угол между прямой B1F1 и плоскостью AF1C1.
Слайд 18№7.Основанием прямой призмы ABCDA1B1C1D1 является ромб с тупым углом B, равным
120°. Все ребра этой призмы равны 10. Точки P и K – середины ребер СС1 и СD соответственно.
а) Докажите, что P K и PB1 перпендикулярны.
б) Найдите угол между плоскостями PKB1 и С1B1B.