г. Мозыря»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Равнобедренный треугольник 7 класс
Содержание
- 1. Презентация по геометрии на тему Равнобедренный треугольник 7 класс
- 2. Цель урока: ввести определение равнобедренного
- 3. Отгадайте ребус Треугольник
- 4. Треугольник называется
- 5. Теорема. (о свойстве углов при основании)В равнобедренном
- 6. Дано: ∆ABC, АВ =BС, ВК
- 7. Дано: ∆ABC, ےА= ےС. Доказать: АВ=ВС.Доказательство. Мысленно
- 8. Доказанный признак равнобедренного треугольника является теоремой, обратной
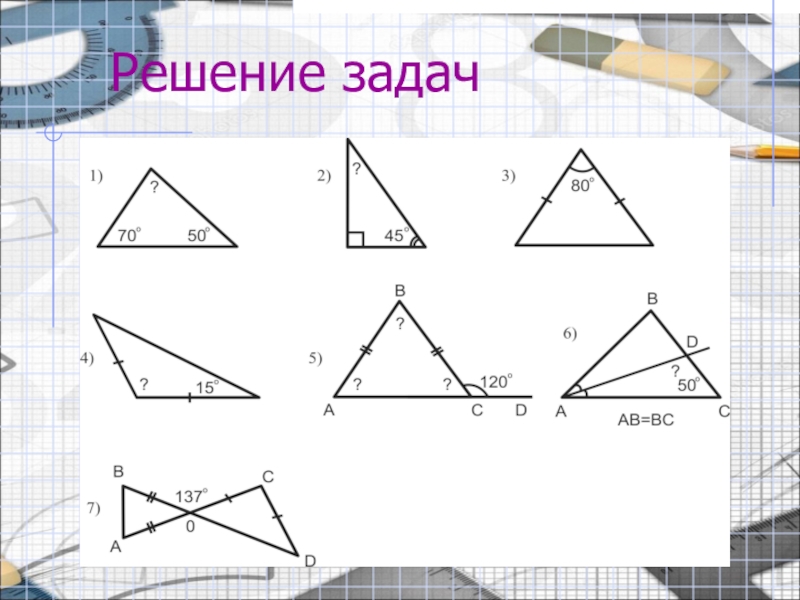
- 9. Решение задачНайдите угол KBA.ےKBA = 70° ےKBA = 40° ےKBA = 110°12 3
- 10. Решение задач
- 11. Слайд 11
- 12. РЕШАЕМ САМОСТОЯТЕЛЬНО№ 83 устно№85№87 (а,б,в)Домашняя работаГлава 2, §11 №84, №86
- 13. Удачи!
Цель урока: ввести определение равнобедренного треугольника и его элементов; познакомится со свойством углов равнобедренного треугольника;научиться пользоваться доказанным свойством при решении задач.
Слайд 1Равнобедренный треугольник
Геометрия 7 класс
Савенок Инна Сергеевна,
учитель математики,
ГУО «Средняя школа №5
Слайд 2 Цель урока:
ввести определение равнобедренного треугольника и его
элементов;
познакомится со свойством углов равнобедренного треугольника;
научиться пользоваться доказанным свойством при решении задач.
познакомится со свойством углов равнобедренного треугольника;
научиться пользоваться доказанным свойством при решении задач.
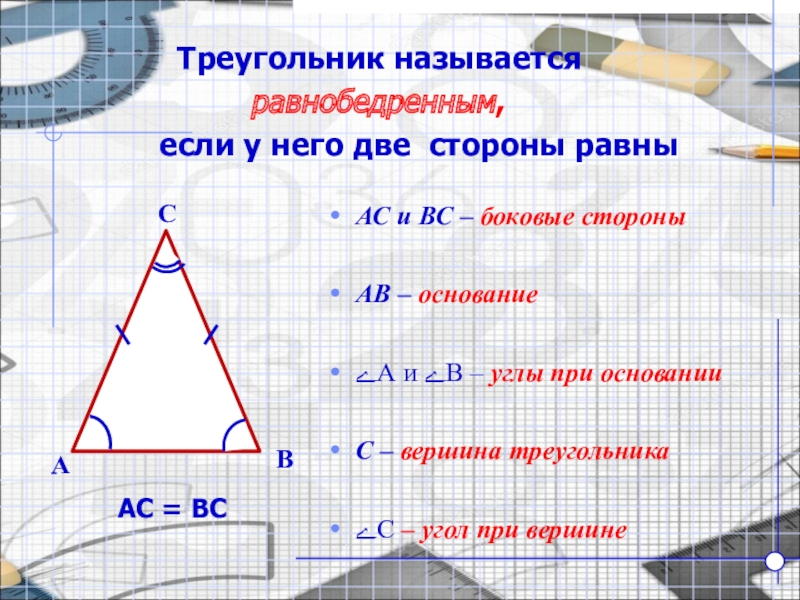
Слайд 4 Треугольник называется
равнобедренным,
если у него две стороны равны
если у него две стороны равны
B
A
C
АС и ВС – боковые стороны
АВ – основание
ےА и ےВ – углы при основании
С – вершина треугольника
ےС – угол при вершине
АС = ВС
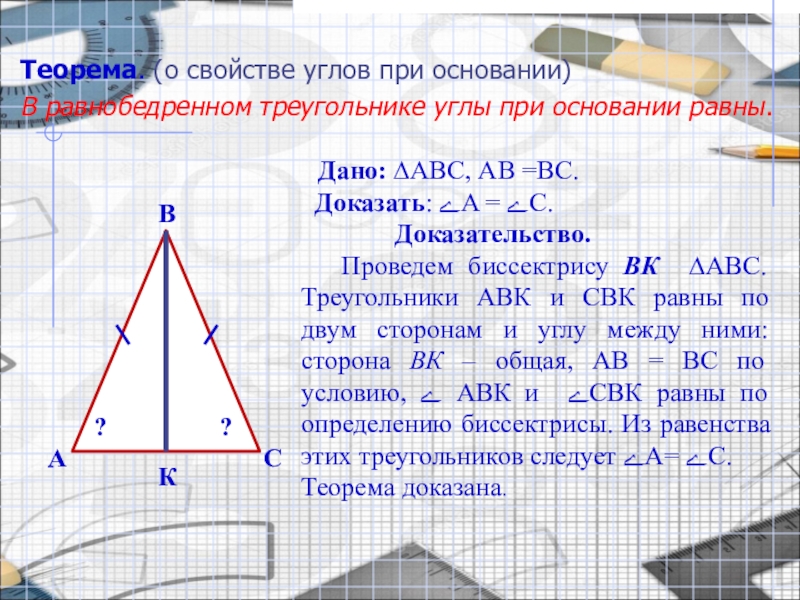
Слайд 5Теорема. (о свойстве углов при основании)
В равнобедренном треугольнике углы при основании
равны.
Дано: ∆ABC, АВ =BС.
Доказать: ےA = ےС.
Доказательство.
Проведем биссектрису ВК ∆ABС. Треугольники АВК и СВК равны по двум сторонам и углу между ними: сторона ВК – общая, АВ = ВС по условию, ے АВК и ےСВК равны по определению биссектрисы. Из равенства этих треугольников следует ےА= ےС.
Теорема доказана.
С
A
В
?
?
К
Слайд 6 Дано: ∆ABC, АВ =BС, ВК - биссектриса.
Доказать: ВК
– медиана и высота.
Доказательство.
Треугольники АВК и СВК равны по двум сторонам и углу между ними: сторона ВК – общая, АВ = ВС по условию, ے АВК и ےСВК равны по определению биссектрисы. Из равенства этих треугольников следует, что АК=КС и ے 1= ے 2. Так как углы 1 2 смежные, то их сумма равна 1800 , поэтому ے 1= ے 2 = 900 . Следовательно ВК- медиана и высота. Теорема доказана.
Доказательство.
Треугольники АВК и СВК равны по двум сторонам и углу между ними: сторона ВК – общая, АВ = ВС по условию, ے АВК и ےСВК равны по определению биссектрисы. Из равенства этих треугольников следует, что АК=КС и ے 1= ے 2. Так как углы 1 2 смежные, то их сумма равна 1800 , поэтому ے 1= ے 2 = 900 . Следовательно ВК- медиана и высота. Теорема доказана.
Теорема. (о свойстве биссектрисы равнобедренного треугольника)
В равнобедренном треугольнике биссектриса, проведенная к основанию, является его медианой и высотой.
С
A
В
1
2
К
Слайд 7Дано: ∆ABC, ےА= ےС.
Доказать: АВ=ВС.
Доказательство. Мысленно перевернем ∆ABC обратной стороной
и наложим перевернутый треугольник на ∆ABC так, чтобы их стороны АС совпадали, угол С совпал с углом А, угол А совпал с углом С. Тогда перевернутый треугольник совместится с данным, и сторона ВС совместится с данным, и сторона ВС совместиться со стороной АВ. Следовательно, АВ=ВС, т.е. ∆ABC- равнобедренный. Теорема доказана.
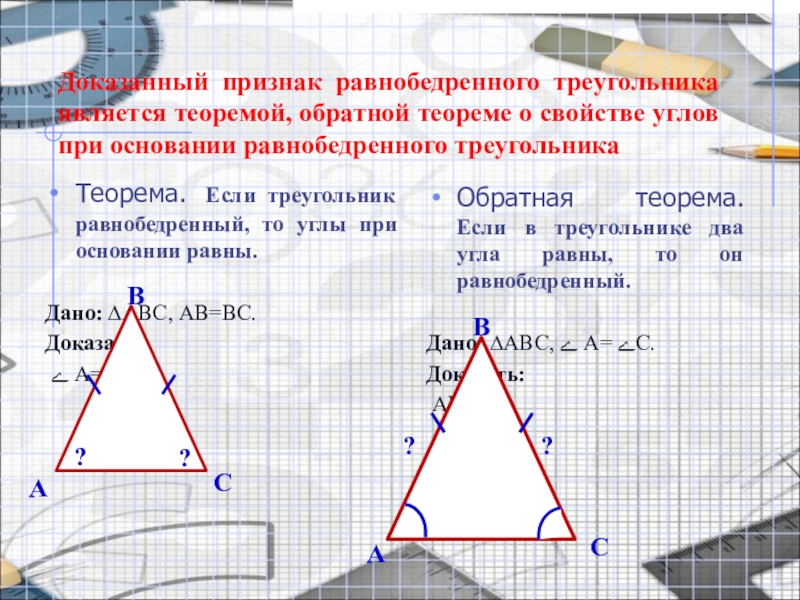
Теорема. (признак равнобедренного треугольника)
Если в треугольнике два угла равны, то он равнобедренный.
С
A
В
В
С
А
Слайд 8Доказанный признак равнобедренного треугольника является теоремой, обратной теореме о свойстве углов
при основании равнобедренного треугольника
Теорема. Если треугольник равнобедренный, то углы при основании равны.
Дано: ∆ABC, АВ=ВС.
Доказать:
ے А= ےС.
Обратная теорема. Если в треугольнике два угла равны, то он равнобедренный.
Дано: ∆ABC, ے А= ےС.
Доказать:
АВ=ВС.
С
A
В
?
?
С
A
В
?
?
