- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК (7 класс)
Содержание
- 1. Презентация по геометрии на тему РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК (7 класс)
- 2. Определение равнобедренного треугольникаТреугольник, две стороны которого равны,
- 3. 1.Какой это треугольник? 2.Назовите основание и
- 4. Определите на глаз
- 5. Дано: АВС равнобедренный
- 6. ТЕОРЕМАВ равнобедренном треугольнике углы при основании равны.
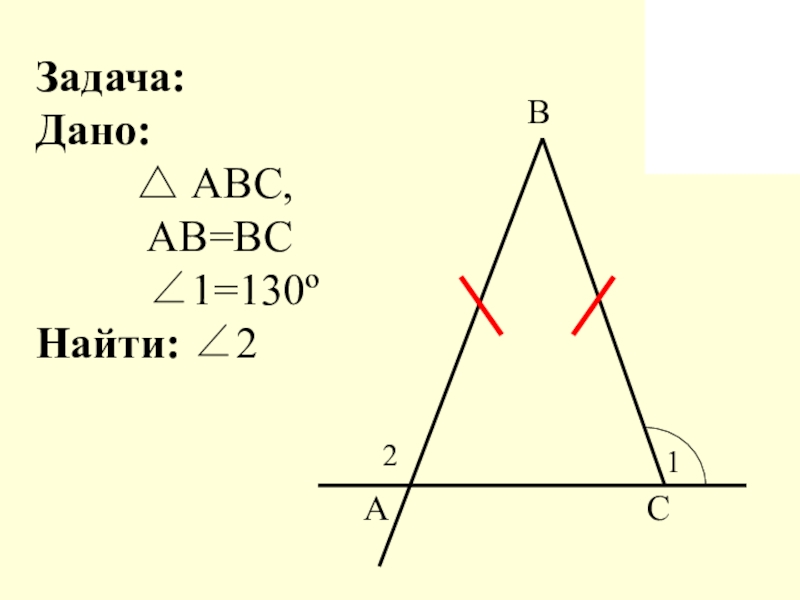
- 7. Задача: Дано:
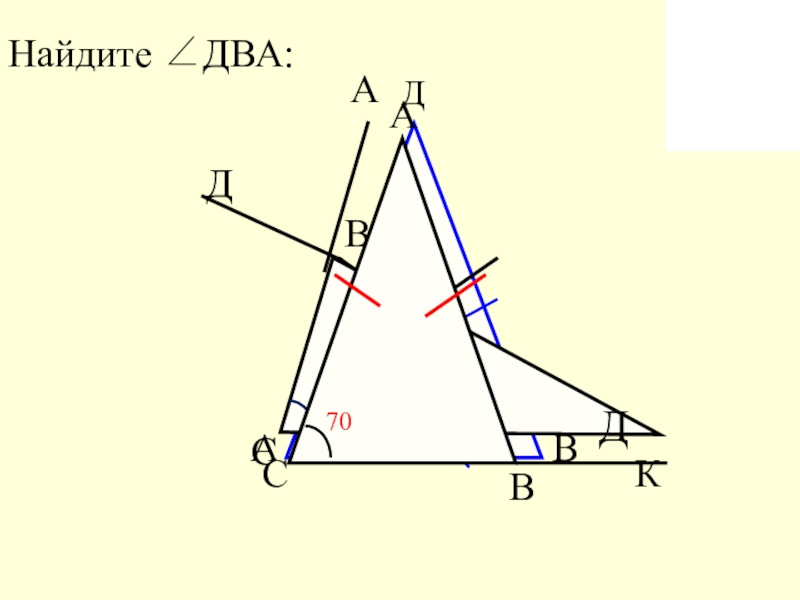
- 8. Найдите ДВА:
- 9. Как известно, биссектриса треугольника делит его угол
- 10. Слайд 10
- 11. Дано: АВС- равнобедренный
- 12. Теоретический тест1. Медиана в равнобедренном треугольнике
- 13. 4.Если треугольник равнобедренный, то:
- 14. Словарь:РавнобедренныйРавностороннийОснованиеБоковая сторона
- 15. спасибо за внимание
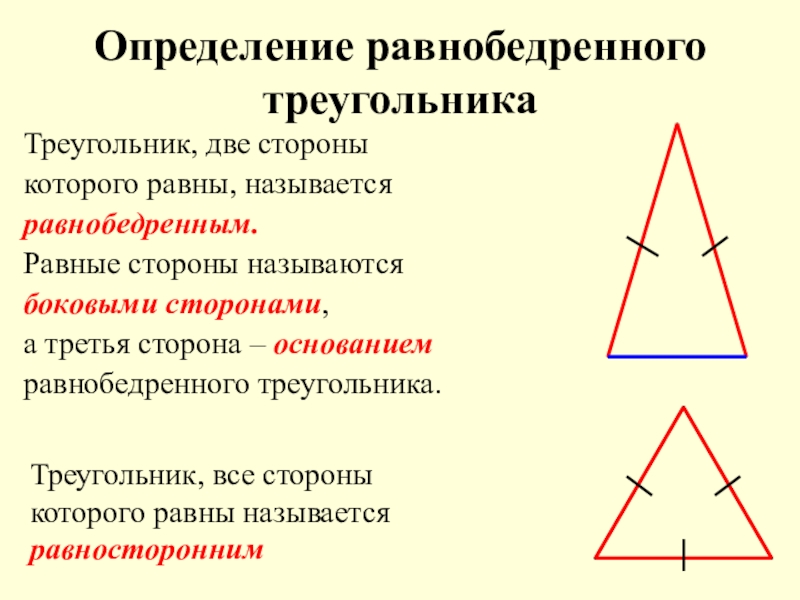
Слайд 2Определение равнобедренного треугольника
Треугольник, две стороны
которого равны, называется
равнобедренным.
Равные стороны называются
боковыми сторонами,
а третья сторона – основанием
равнобедренного треугольника.
Треугольник, все стороны которого равны называется
равносторонним
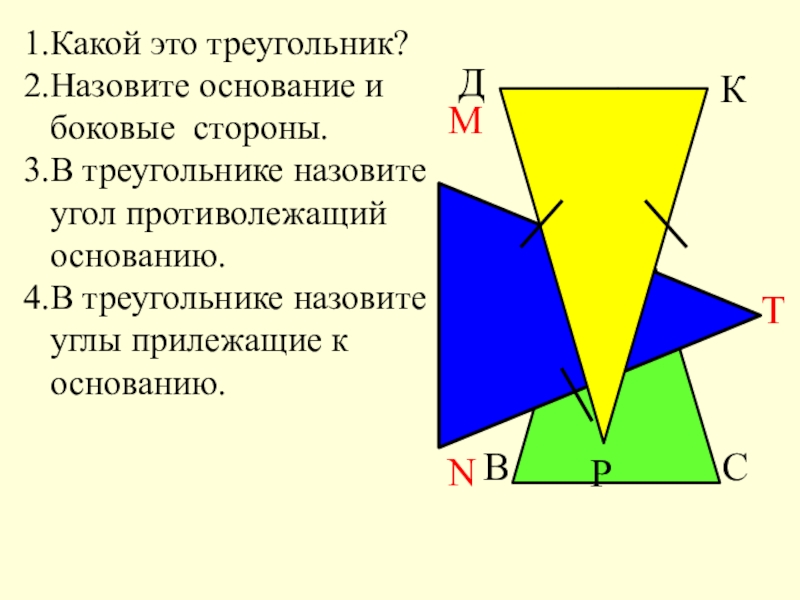
Слайд 31.Какой это треугольник? 2.Назовите основание и боковые стороны. 3.В треугольнике
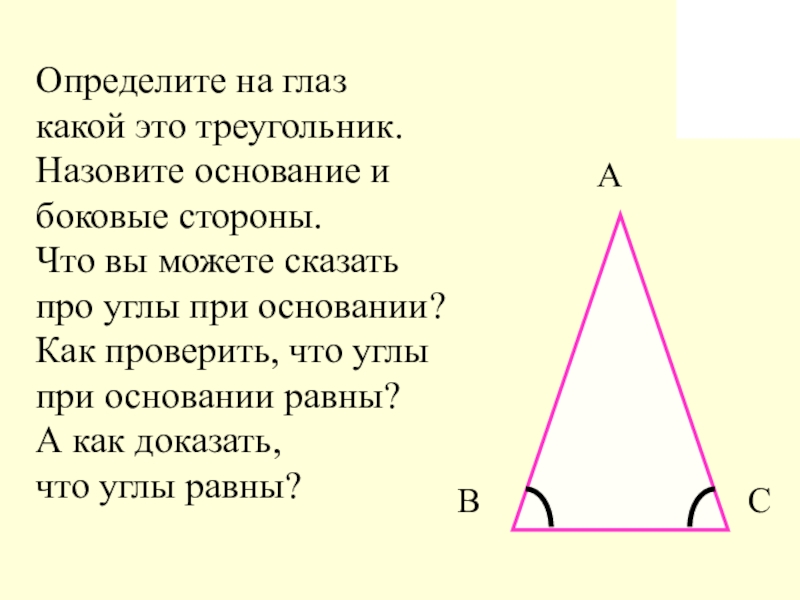
Слайд 4Определите на глаз
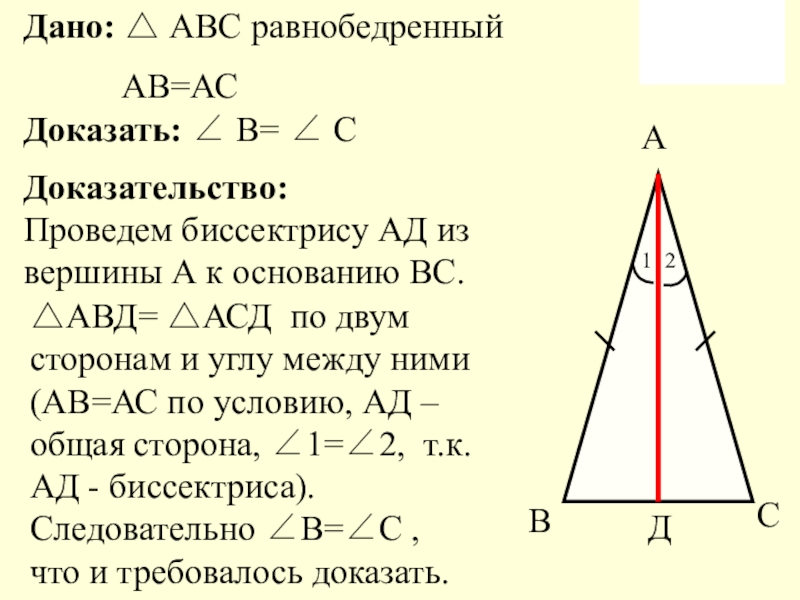
Слайд 5Дано: АВС равнобедренный
АВ=АС
Доказать:
Доказательство: Проведем биссектрису АД из вершины А к основанию ВС.
В
С
А
АВД= АСД по двум сторонам и углу между ними (АВ=АС по условию, АД – общая сторона, 1=2, т.к. АД - биссектриса). Следовательно В=С , что и требовалось доказать.
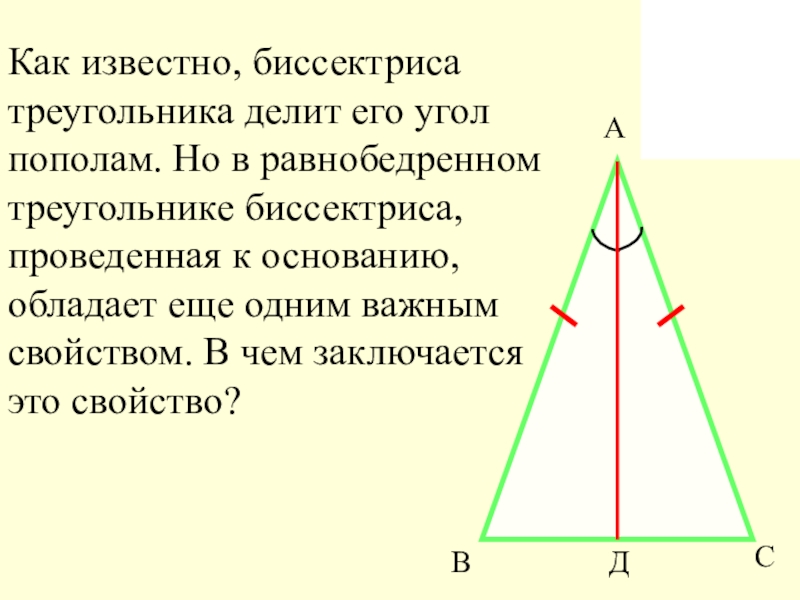
Слайд 9Как известно, биссектриса треугольника делит его угол пополам. Но в равнобедренном
А
В
С
Слайд 10 ТЕОРЕМА В равнобедренном треугольнике биссектриса,
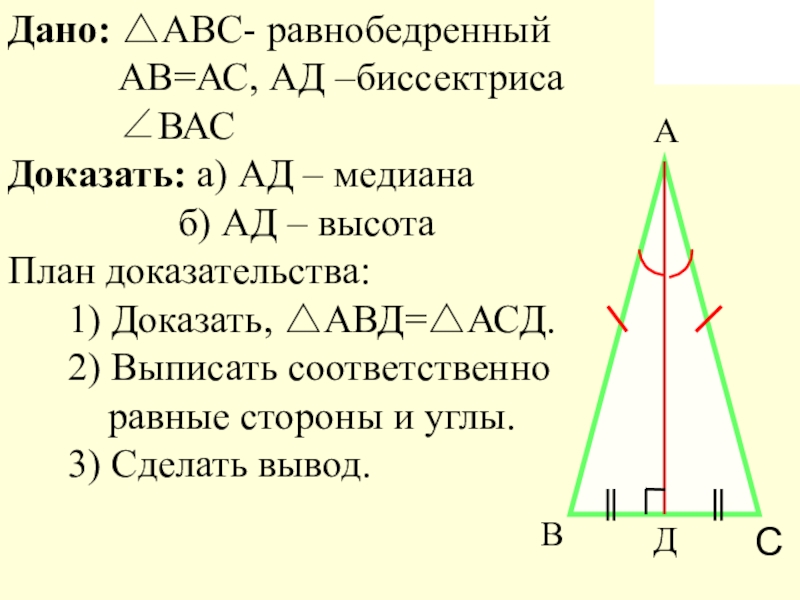
Слайд 11Дано: АВС- равнобедренный
АВ=АС, АД –биссектриса
ВАС
Доказать: а) АД – медиана
б) АД – высота
План доказательства:
1) Доказать, АВД=АСД.
2) Выписать соответственно
равные стороны и углы.
3) Сделать вывод.
В
А
С
Слайд 12Теоретический тест
1. Медиана в равнобедренном треугольнике
является его
Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
2. Если треугольник равносторонний, то:
а) он равнобедренный;
б) все его углы равны;
в) любая его высота является
биссектрисой и медианой.
3. Биссектриса в равнобедренном
треугольнике является медианой и
высотой. Этот утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
Слайд 134.Если треугольник равнобедренный,
то:
а) он равносторонний;
биссектрисой и высотой;
в) ответы а) и б) неверны.
5. В каком треугольнике только одна
его высота делит треугольник на два
равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем.
Ответы:
1-б); 2-а), б), в); 3-б); 4-в); 5-б).