Презентация, доклад по геометрии на тему Прямоугольный параллелепипед (10 класс)

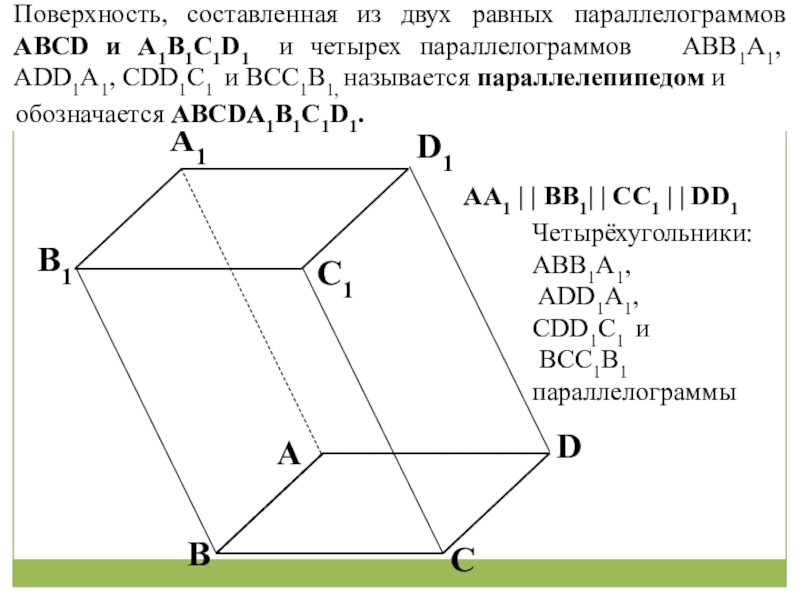
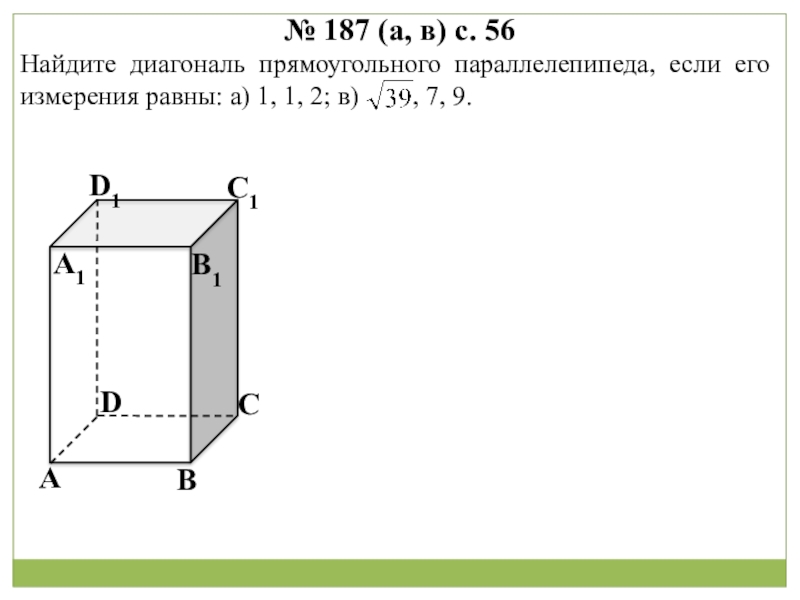
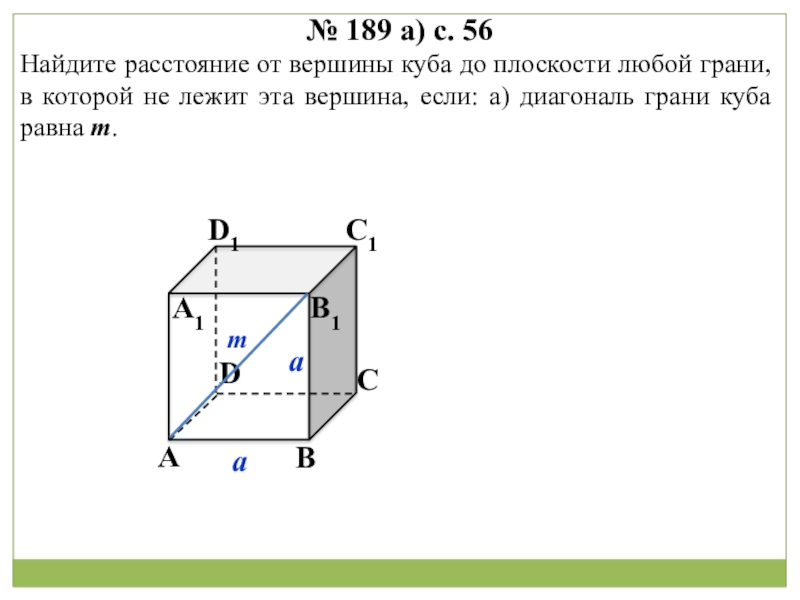
АА1   ВB1  CC1   DD1

Поверхность, составленная из двух равных параллелограммов АВСD и A1B1C1D1 и четырех параллелограммов АВВ1А1, ADD1A1, CDD1C1 и ВСС1В1, называется параллелепипедом и

Четырёхугольники:
АВВ1А1,
ADD1A1,
CDD1C1 и
ВСС1В1
параллелограммы

обозначается АВСDA1B1C1D1.

с. 56

Прямоугольный параллелепипед

основания представляют собой прямоугольники.

Докажите, что боковые грани – прямоугольники.

Свойства прямоугольного параллелепипеда:

1. В прямоугольном параллелепипеде все шесть граней – прямоугольники.

2. Все двугранные углы прямоугольного параллелепипеда – прямые.

Длины трёх рёбер, имеющих общую вершину, называются измерениями прямоугольного параллелепипеда.

длина

ширина

в
ы
с
о
т
а

3. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

= АВ2 + ВС2 + ВВ12

Доказать:

АС12 = АС2 + СС12

Доказательство:

АС2 = АВ2 + ВС2

АС12 = АВ2 + ВС2 + СС12

ВВ1 = СС1

АС12 = АВ2 + ВС2 + ВВ12

параллелепипеда равен сумме квадратов трёх его измерений.

измерения равны: а) 1, 1, 2; в) , 7, 9.

4. Диагональ параллелепипеда равна 6. Найдите третье ребро, выходящее из той же вершины.

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 4. Диагональ параллелепипеда равна 6. Найдите третье ребро, выходящее из той же вершины.

ЕГЭ профиль задание 8

куба.

a

a

любой грани, в которой не лежит эта вершина, если: а) диагональ грани куба равна т.

т

a

a

прямоугольном параллелепипеде все шесть граней – прямоугольники.
2) Все двугранные углы прямоугольного параллелепипеда – прямые.
3) Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.