- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Прямоугольные треугольники
Содержание
- 1. Презентация по геометрии на тему Прямоугольные треугольники
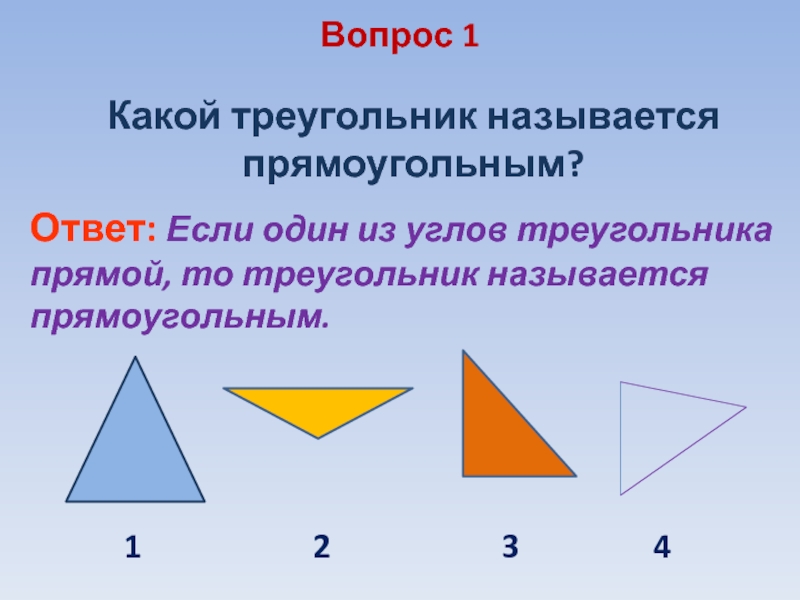
- 2. Вопрос 1Какой треугольник называется прямоугольным? Ответ: Если один из углов треугольника прямой, то треугольник называется прямоугольным.1243
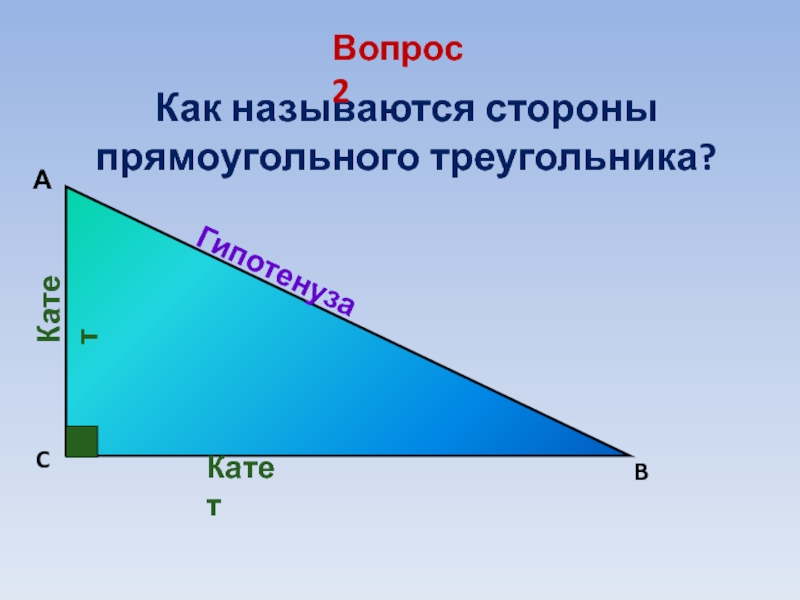
- 3. C B А ГипотенузаКатетКатетКак называются стороны прямоугольного треугольника?Вопрос 2
- 4. Назовите свойства прямоугольного треугольника.Вопрос 3Сумма острых углов
- 5. Решение задач по готовым чертежам
- 6. Решение задач по готовым чертежам1.Дано:
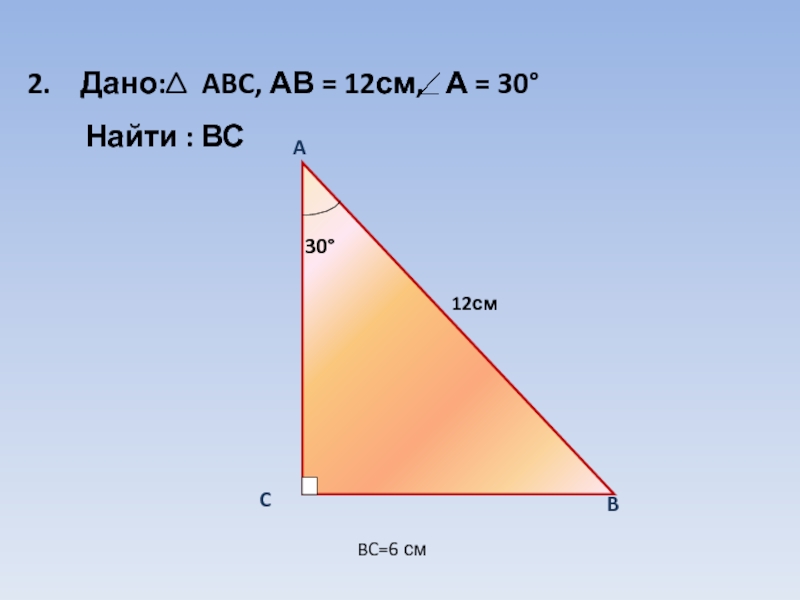
- 7. Дано: ABC, АВ = 12см,
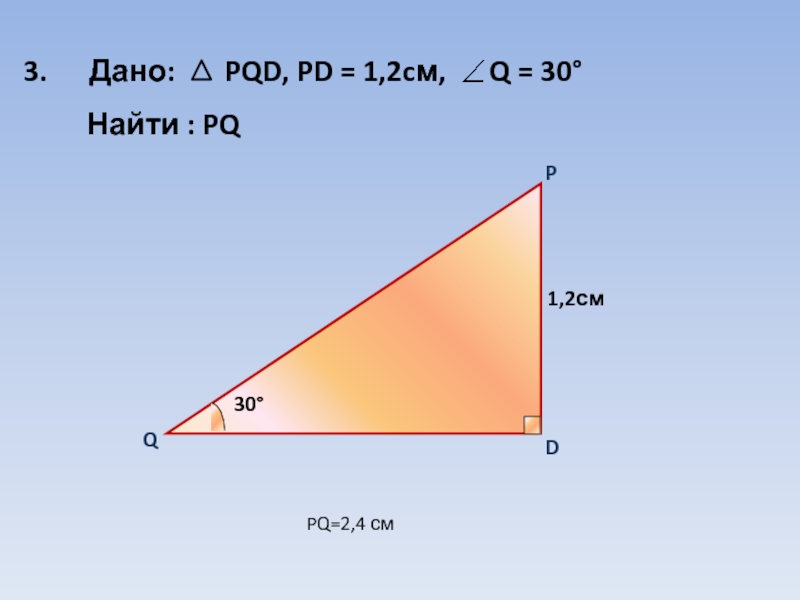
- 8. 3. Дано:
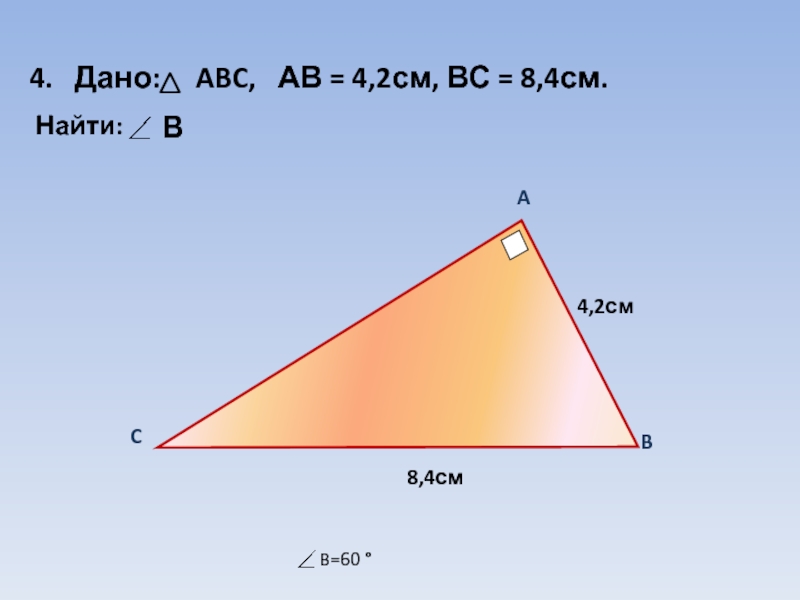
- 9. A4,2см8,4смBC4. Дано: ABC, АВ = 4,2см, ВС = 8,4см. Найти:ВB=60
- 10. Признаки равенства треугольников.Теорема. Если две стороны
- 11. Признаки равенства Прямоугольных треугольников
- 12. Признаки равенства прямоугольных треугольников.ABCA1B1C1А C B А1
- 13. Теорема1Если гипотенуза и острый угол одного прямоугольного
- 14. Теорема2Если гипотенуза и катет одного прямоугольного треугольника
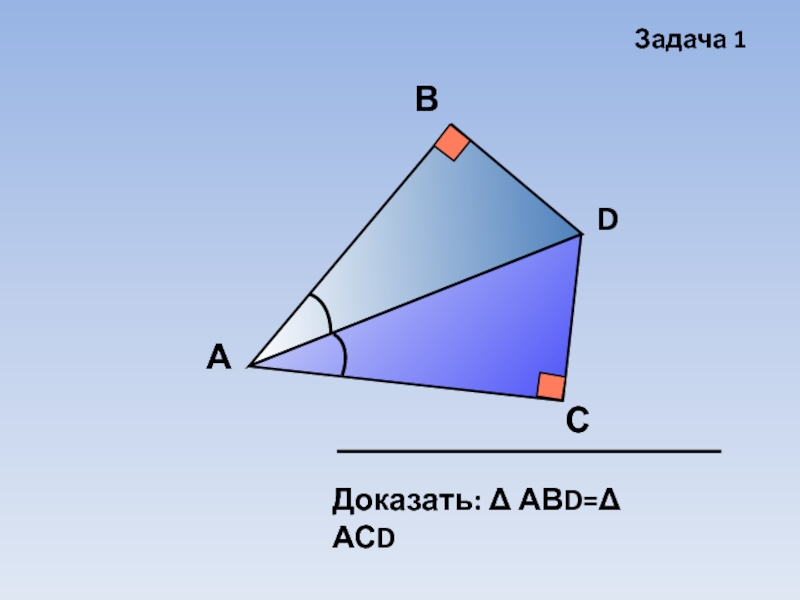
- 15. Задача 1АВСDДоказать: Δ АВD=Δ АСD
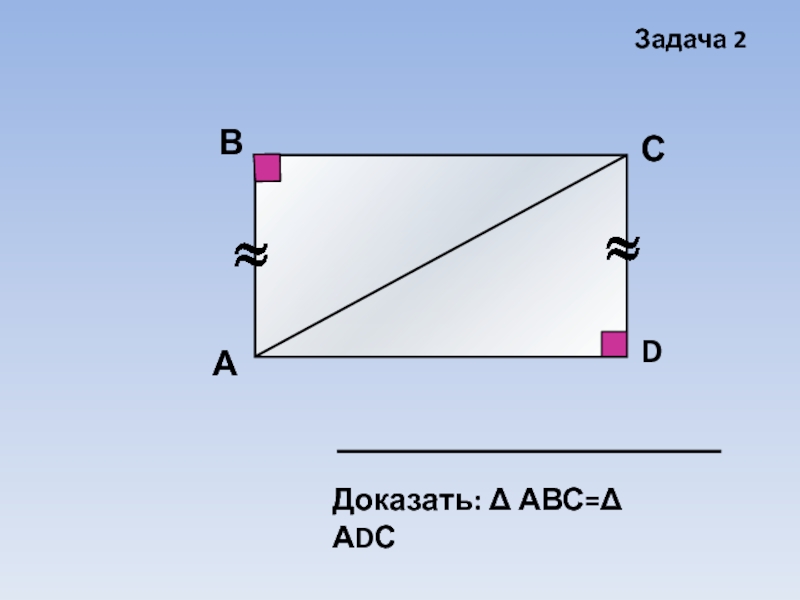
- 16. АВСDДоказать: Δ АВС=Δ АDСЗадача 2
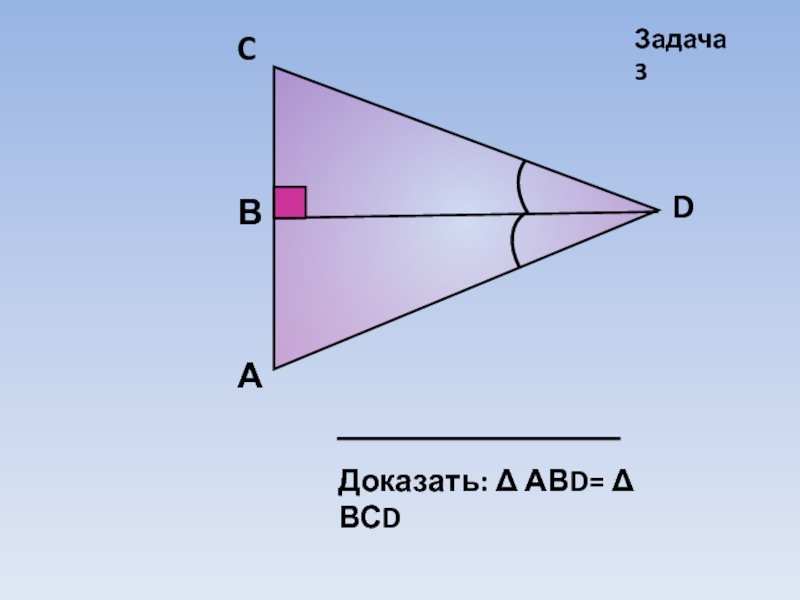
- 17. АDВCДоказать: Δ АВD= Δ ВСDЗадача 3
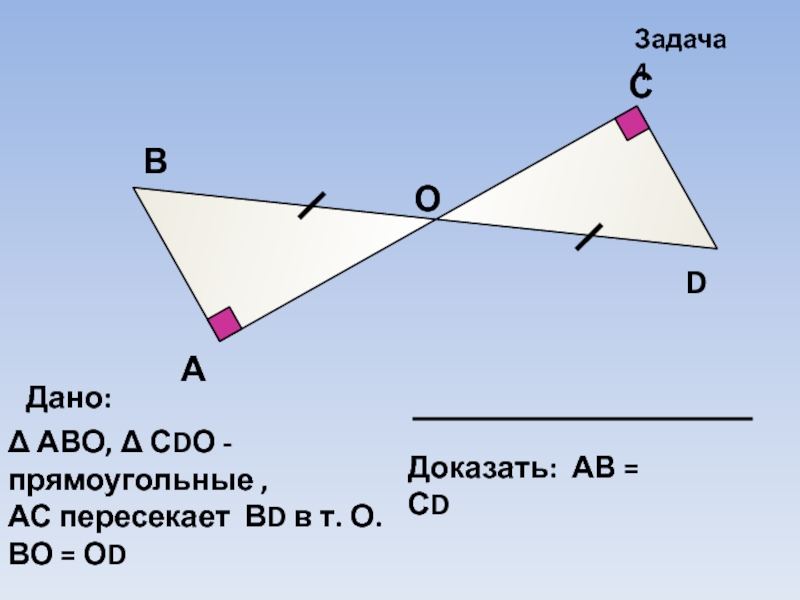
- 18. АВСDЗадача 4ОДано:Δ АВО, Δ СDО - прямоугольные ,АС пересекает ВD в т. О. ВО = ОD
- 19. Самостоятельная работа1. Дано: ∆ABC,BD – высота,
- 20. Самостоятельная работа Дано: ∆ABC,BD
- 21. Домашнее задание:
- 22. Признаки равенства прямоугольных треугольников.АCB А1 C1 B1
Слайд 2Вопрос 1
Какой треугольник называется прямоугольным?
Ответ: Если один из углов треугольника
1
2
4
3
Слайд 4Назовите свойства прямоугольного треугольника.
Вопрос 3
Сумма острых углов прямоугольного треугольника равна 90°
Катет
Если катет равен половине гипотенузы то он лежит против угла в 30°.
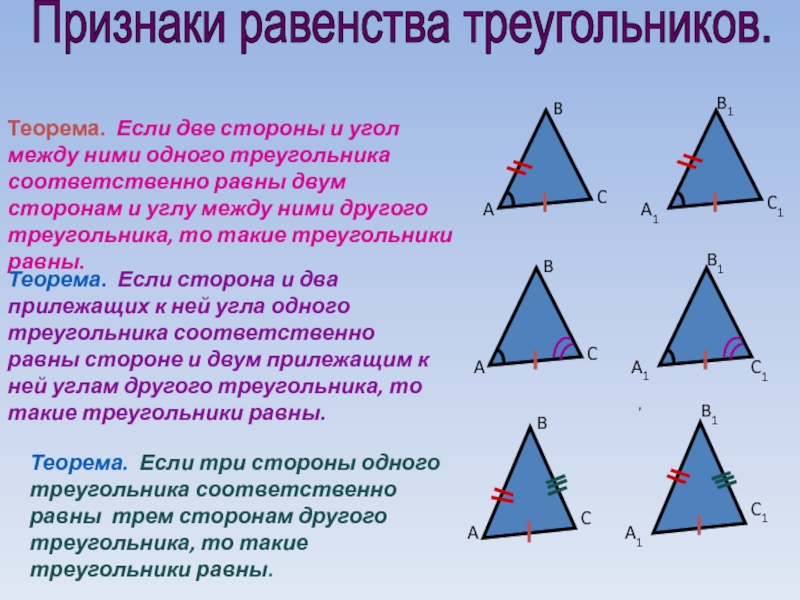
Слайд 10 Признаки равенства треугольников.
Теорема. Если две стороны и угол между ними
Теорема. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Теорема. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
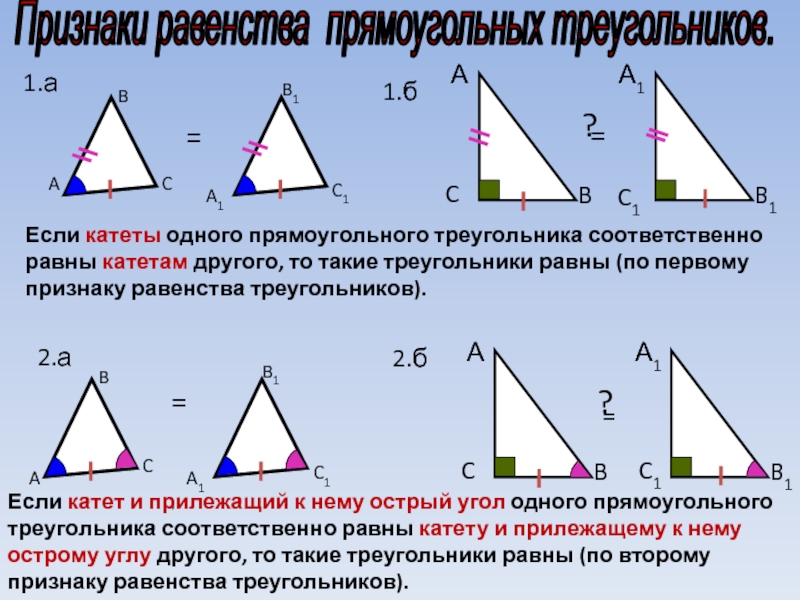
Слайд 12Признаки равенства прямоугольных треугольников.
A
B
C
A1
B1
C1
А
C
B
А1
C1
B1
1.а
1.б
2.б
2.а
=
?
Если катеты
A
B
C
A1
B1
А
C
B
А1
C1
B1
?
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны (по второму признаку равенства треугольников).
=
=
=
C1
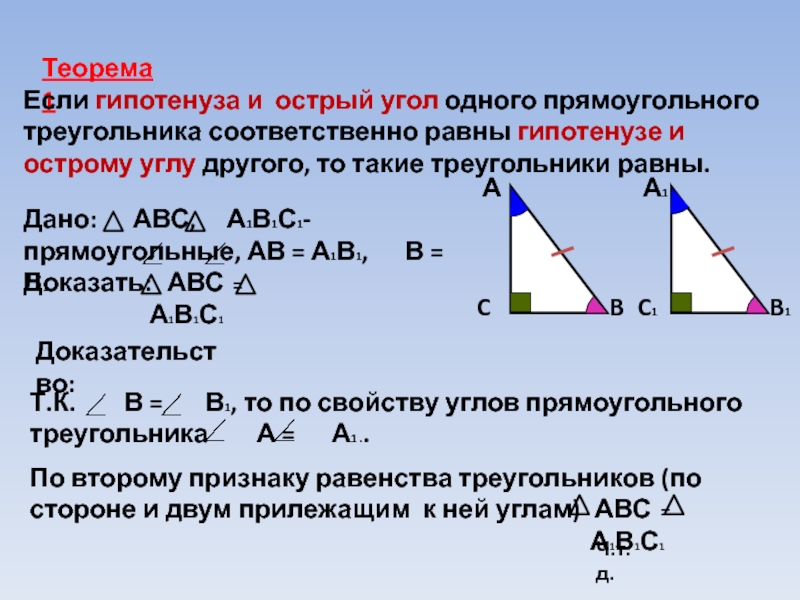
Слайд 13Теорема1
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе
Дано: АВС, А1В1С1- прямоугольные, АВ = А1В1, В = В1
Доказать:
АВС = А1В1С1
Доказательство:
Т.К. В = В1, то по свойству углов прямоугольного треугольника А = А1 ..
По второму признаку равенства треугольников (по стороне и двум прилежащим к ней углам)
АВС = А1В1С1
Ч.т.д.
Слайд 14Теорема2
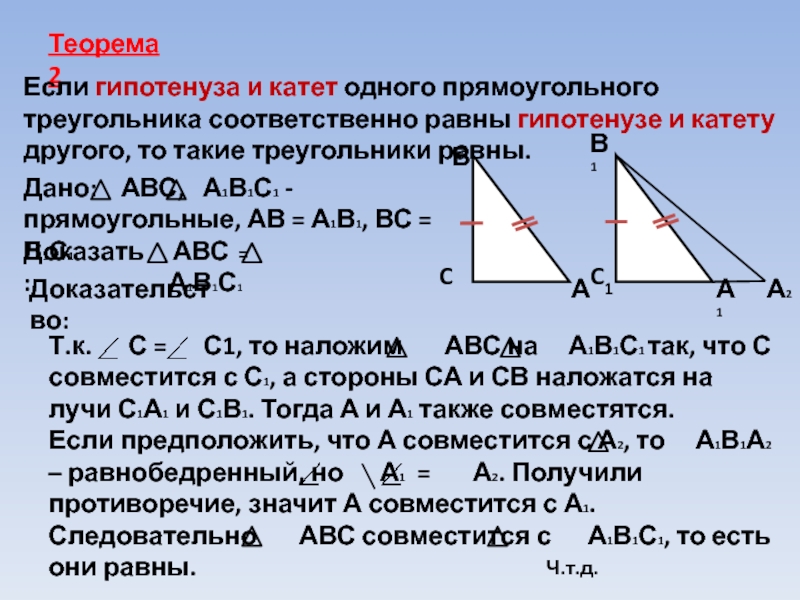
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и
Дано: АВС, А1В1С1 - прямоугольные, АВ = А1В1, ВС = В1С1
Доказать:
АВС = А1В1С1
Доказательство:
Т.к. С = С1, то наложим АВС на А1В1С1 так, что С совместится с С1, а стороны СА и СВ наложатся на лучи С1А1 и С1В1. Тогда А и А1 также совместятся.
Если предположить, что А совместится с А2, то А1В1А2 – равнобедренный, но А1 = А2. Получили противоречие, значит А совместится с А1.
Следовательно АВС совместится с А1В1С1, то есть они равны.
Ч.т.д.
А2
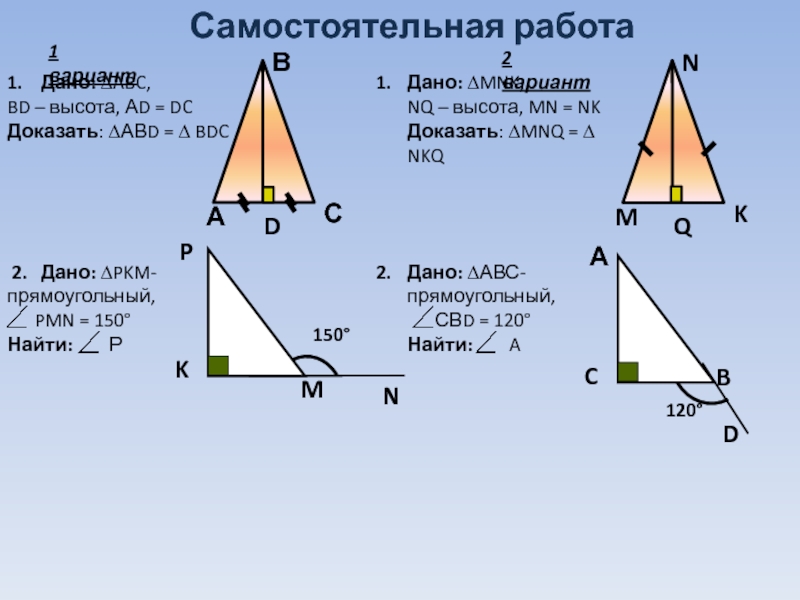
Слайд 19Самостоятельная работа
1. Дано: ∆ABC,
BD – высота, АD = DC
Доказать: ∆АВD
Дано: ∆MNK,
NQ – высота, MN = NK
Доказать: ∆MNQ = ∆ NKQ
2. Дано: ∆PKM-прямоугольный,
PMN = 150
Найти: Р
Дано: ∆АВС-прямоугольный,
СВD = 120
Найти: A
1 вариант
2 вариант
1.
2.
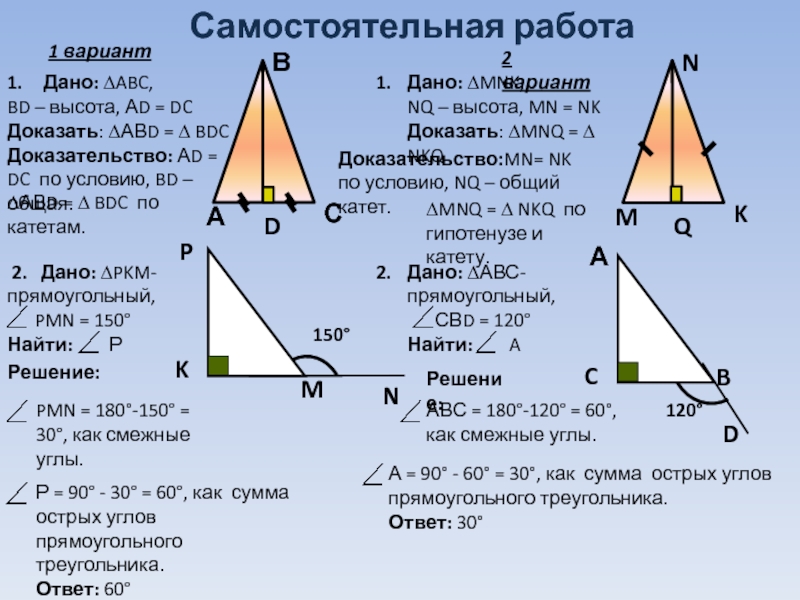
Слайд 20Самостоятельная работа
Дано: ∆ABC,
BD – высота, АD =
Доказать: ∆АВD = ∆ BDC
Доказательство: АD = DC по условию, BD – общая.
Дано: ∆MNK,
NQ – высота, MN = NK
Доказать: ∆MNQ = ∆ NKQ
2. Дано: ∆PKM-прямоугольный,
PMN = 150
Найти: Р
Дано: ∆АВС-прямоугольный,
СВD = 120
Найти: A
∆АВD = ∆ BDC по
катетам.
1.
1.
2.
1 вариант
2 вариант
Доказательство:MN= NK по условию, NQ – общий катет.
∆MNQ = ∆ NKQ по гипотенузе и катету.
PMN = 180°-150 = 30°, как смежные углы.
Р = 90° - 30° = 60°, как сумма острых углов прямоугольного треугольника.
Ответ: 60°
Решение:
Решение:
АВС = 180°-120 = 60°,
как смежные углы.
А = 90° - 60° = 30°, как сумма острых углов прямоугольного треугольника.
Ответ: 30°
Слайд 22Признаки равенства прямоугольных треугольников.
А
C
B
А1
C1
B1
1.
=
2.
А
C
B
А1
C1
=
B1
Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны (по первому признаку равенства треугольников).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны (по второму признаку равенства треугольников).
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
А
C
B
А1
C1
B1
4.
3.
А1
C1
B1
=
=
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.