- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Произведения отрезков хорд и секущих
Содержание
- 1. Презентация по геометрии на тему Произведения отрезков хорд и секущих
- 2. 19. 04. 18 Классная работаПроизведения отрезков хорд и секущих.
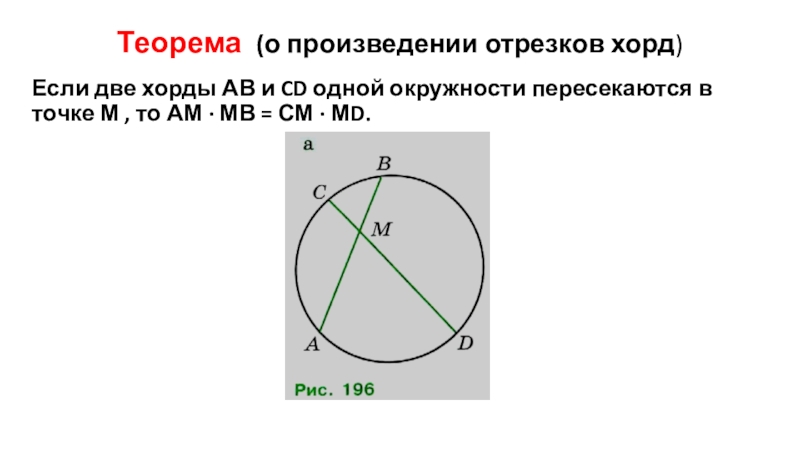
- 3. Теорема (о произведении отрезков хорд)Если две хорды
- 4. Слайд 4
- 5. Интересно, что равенство, доказанное в теореме о
- 6. Теорема (о произведении отрезков секущих). Если из
- 7. Представим себе, что секущий луч МС, вращаясь
- 8. Теорема (о квадрате касательной). Квадрат отрезка касательной
- 9. Проекции катетов на гипотенузу Так как высота,
- 10. 1) Свойство высоты, проведенной к гипотенузе.Высота прямоугольного треугольника,
- 11. Слайд 11
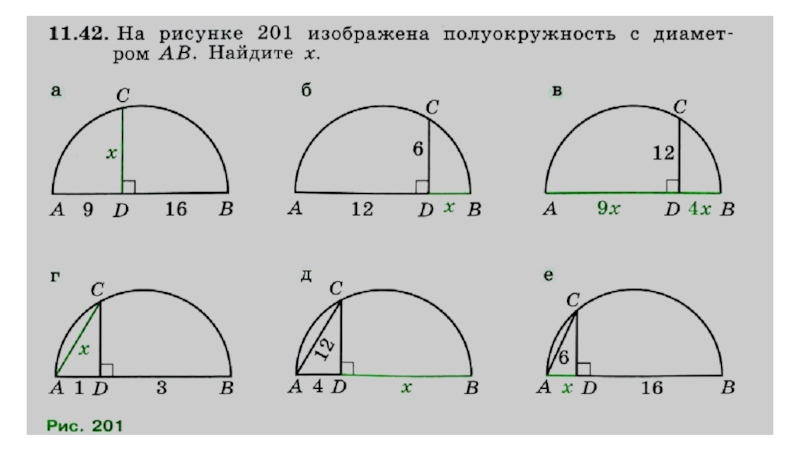
- 12. № 11. 42(а)
- 13. Слайд 13
- 14. Домашнее заданиеn. 11. 5 (выучить)№ 11. 42(б, г, д, е)
19. 04. 18 Классная работаПроизведения отрезков хорд и секущих.
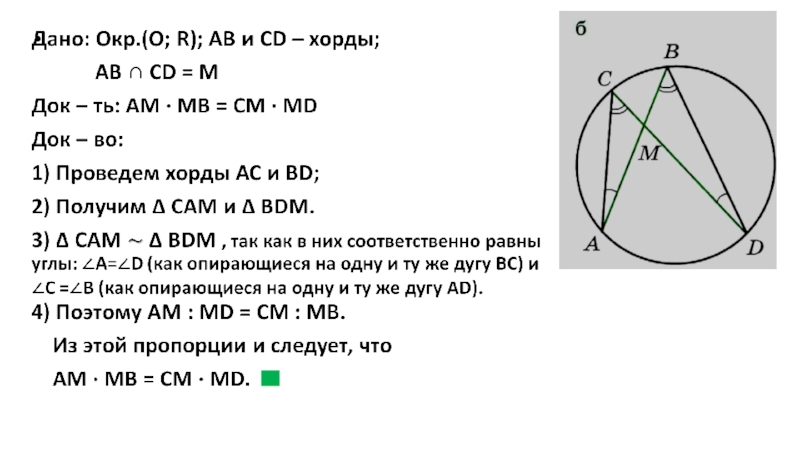
Слайд 3Теорема (о произведении отрезков хорд)
Если две хорды АВ и CD одной
окружности пересекаются в точке М , то АМ · МВ = СМ · МD.
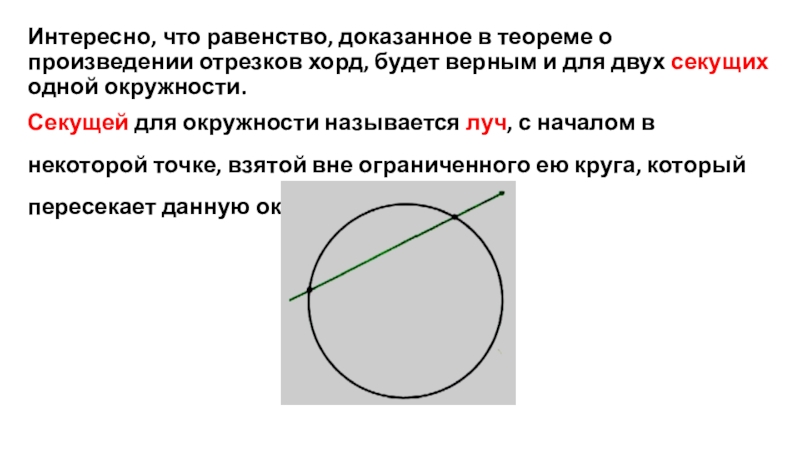
Слайд 5Интересно, что равенство, доказанное в теореме о произведении отрезков хорд, будет
верным и для двух секущих одной окружности.
Секущей для окружности называется луч, с началом в некоторой точке, взятой вне ограниченного ею круга, который пересекает данную окружность.
Секущей для окружности называется луч, с началом в некоторой точке, взятой вне ограниченного ею круга, который пересекает данную окружность.
Слайд 6Теорема (о произведении отрезков секущих).
Если из точки М вне окружности
проведены две секущие, одна из которых пересекают окружность в точках А и В, а другая - в точках С и D, то АМ · МВ = СМ · МD.
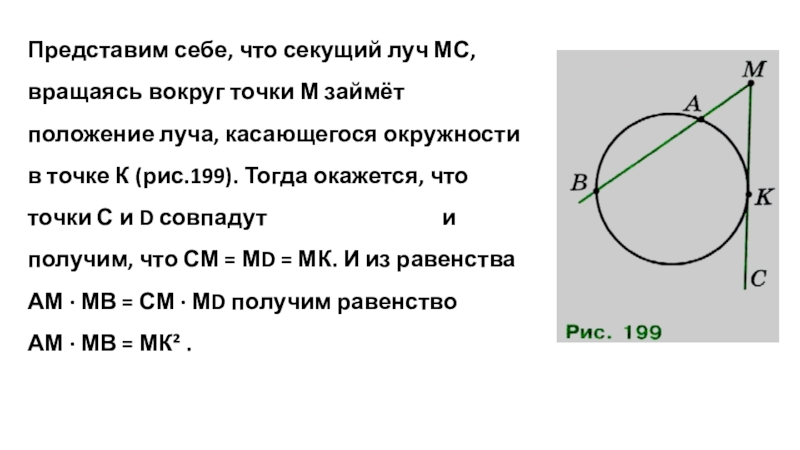
Слайд 7Представим себе, что секущий луч МС, вращаясь вокруг точки М займёт
положение луча, касающегося окружности в точке К (рис.199). Тогда окажется, что точки С и D совпадут и получим, что СМ = МD = МК. И из равенства АМ · МВ = СМ · МD получим равенство АМ · МВ = МК² .
Слайд 8Теорема (о квадрате касательной).
Квадрат отрезка касательной MK, проведённой из некоторой
точки M вне окружности, до точки касания К равен произведению отрезка секущей МВ окружности на внешнюю часть МА этой секущей.
Слайд 9Проекции катетов на гипотенузу
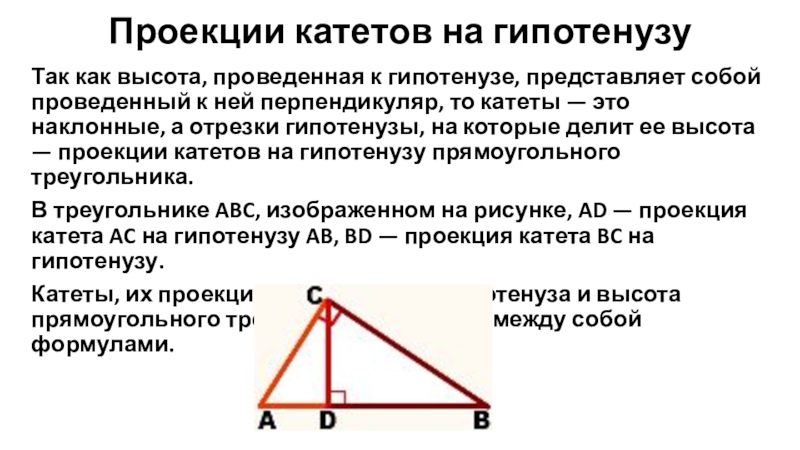
Так как высота, проведенная к гипотенузе, представляет собой
проведенный к ней перпендикуляр, то катеты — это наклонные, а отрезки гипотенузы, на которые делит ее высота — проекции катетов на гипотенузу прямоугольного треугольника.
В треугольнике ABC, изображенном на рисунке, AD — проекция катета AC на гипотенузу AB, BD — проекция катета BC на гипотенузу.
Катеты, их проекции на гипотенузу, гипотенуза и высота прямоугольного треугольника связаны между собой формулами.
В треугольнике ABC, изображенном на рисунке, AD — проекция катета AC на гипотенузу AB, BD — проекция катета BC на гипотенузу.
Катеты, их проекции на гипотенузу, гипотенуза и высота прямоугольного треугольника связаны между собой формулами.
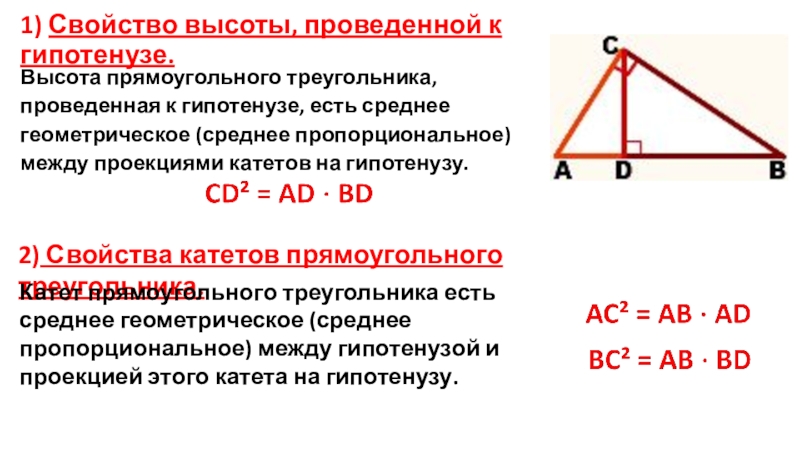
Слайд 101) Свойство высоты, проведенной к гипотенузе.
Высота прямоугольного треугольника, проведенная к гипотенузе, есть
среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу.
2) Свойства катетов прямоугольного треугольника.
Катет прямоугольного треугольника есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.