:
«Признаки равенства прямоугольных треугольников»
учителя математики
ГБОУ школы №1056
Романенко Елены Алексеевны
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Признаки равенства прямоугольных треугольников
Содержание
- 1. Презентация по геометрии на тему Признаки равенства прямоугольных треугольников
- 2. Признаки равенства прямоугольных треугольников
- 3. По катету и прилежащему острому углу
- 4. Если катет и прилежащий к нему острый
- 5. Доказательство:Так как ∆ABC и ∆A1B1C1- прямоугольные, тоА
- 6. По двум катетам
- 7. Если два катета одного прямоугольного треугольника соответственно
- 8. Доказательство:Так как ∆ABC и ∆A1B1C1- прямоугольные, тоА
- 9. По катету и гипотенузе
- 10. Если катет и гипотенуза одного прямоугольного треугольника
- 11. Доказательство:Пусть ∆АВС и ∆А1В1С1 – данные треугольники.
- 12. По гипотенузе и острому углу
- 13. Если гипотенуза и острый угол одного прямоугольного
- 14. Доказательство:1) Так как ∆ABC и ∆A1B1C1- прямоугольные,
Признаки равенства прямоугольных треугольников
Слайд 1Департамент образования города Москвы
Северо-Западное окружное управление образования
Презентация по геометрии на тему
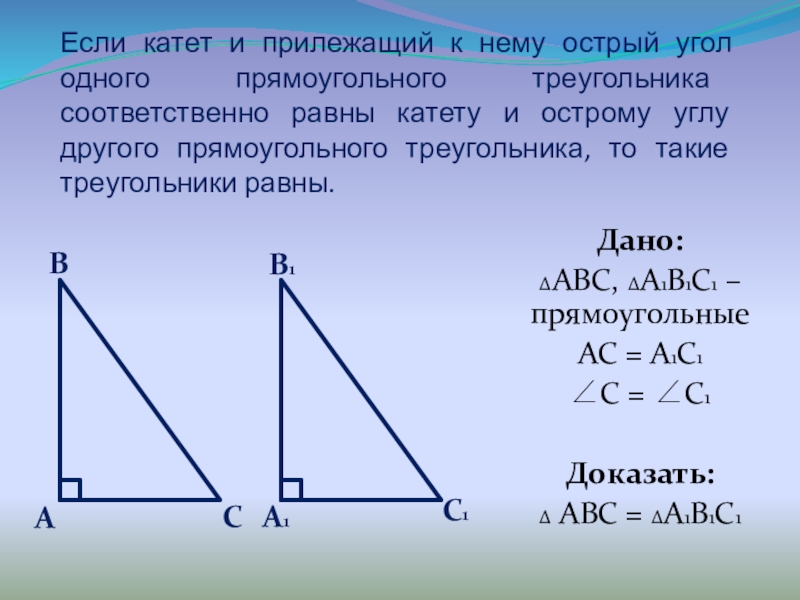
Слайд 4Если катет и прилежащий к нему острый угол одного прямоугольного треугольника
соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Дано:
ΔABC, ΔA1B1C1 – прямоугольные
AC = A1C1
C = C1
Доказать:
Δ ABC = ΔA1B1C1
Слайд 5Доказательство:
Так как ∆ABC и ∆A1B1C1- прямоугольные, то
А = А1 = 90°
С
= С1 (по условию) ∆ABC = ∆A1B1C1
АС = А1С1 (по условию) (по II признаку)
ч.т.д.
АС = А1С1 (по условию) (по II признаку)
ч.т.д.
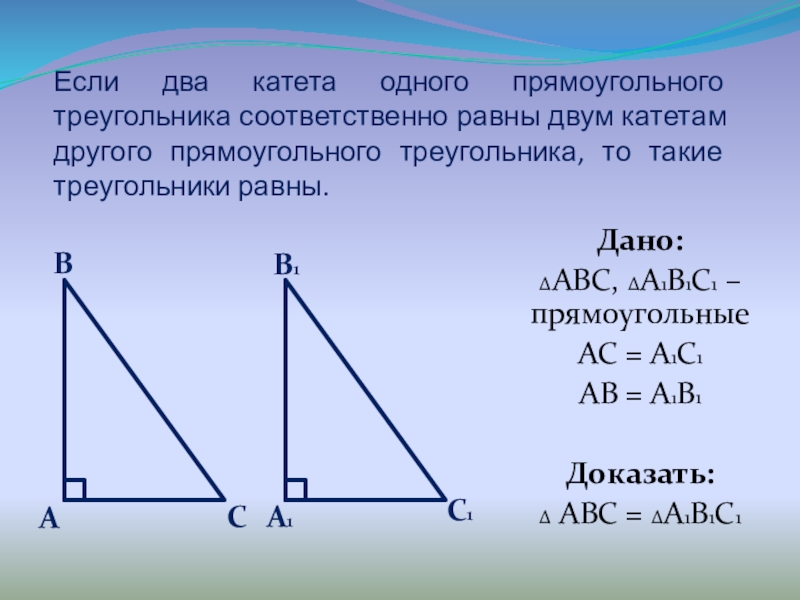
Слайд 7Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого
прямоугольного треугольника, то такие треугольники равны.
Дано:
ΔABC, ΔA1B1C1 – прямоугольные
AC = A1C1
AB = A1B1
Доказать:
Δ ABC = ΔA1B1C1
Слайд 8Доказательство:
Так как ∆ABC и ∆A1B1C1- прямоугольные, то
А = А1 = 90°
АВ
= А1В1 (по условию) ∆ABC = ∆A1B1C1
АС = А1С1 (по условию) (по I признаку)
ч.т.д.
АС = А1С1 (по условию) (по I признаку)
ч.т.д.
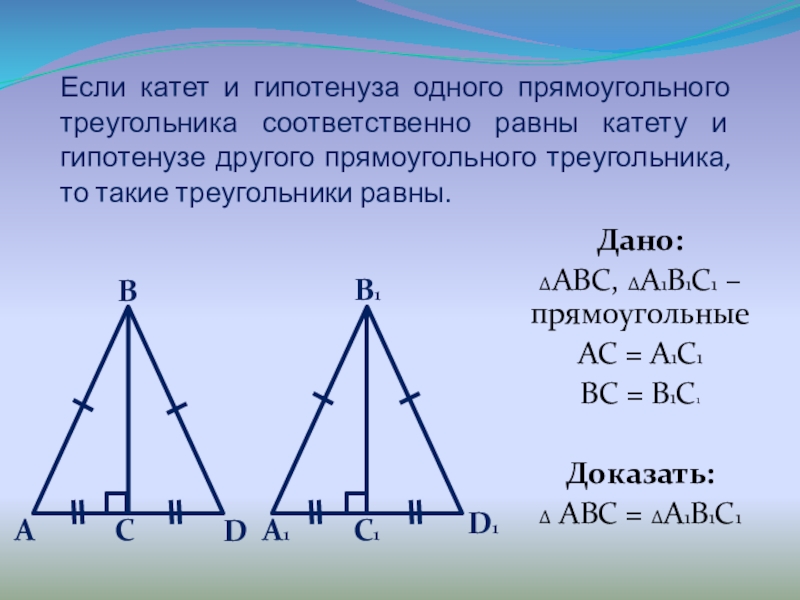
Слайд 10Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и
гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Дано:
ΔABC, ΔA1B1C1 – прямоугольные
AC = A1C1
BC = B1C1
Доказать:
Δ ABC = ΔA1B1C1
A
С
A1
С1
B
D1
B1
D
Слайд 11Доказательство:
Пусть ∆АВС и ∆А1В1С1 – данные треугольники. Построим треугольник ∆CBD, равный
треугольнику ∆СВА и треугольник ∆C1D1B1, равный треугольнику ∆C1A1B1.
Треугольники ∆ABD и ∆A1B1D1 равны по третьему признаку. У них АВ = А1В1 по условию задачи; AD = A1D1, так как АС = А1С1; BD = B1D1, так как BD = AB, B1D1 = A1B1. Из равенства треугольников ∆ABD и ∆A1B1D1 следует равенство углов: A = А1.
Так как по условию АВ = А1В1, АС = А1С1, а A = А1 по доказанному, то треугольники ∆АВС и ∆А1В1С1 равны по первому признаку.
ч.т.д.
Треугольники ∆ABD и ∆A1B1D1 равны по третьему признаку. У них АВ = А1В1 по условию задачи; AD = A1D1, так как АС = А1С1; BD = B1D1, так как BD = AB, B1D1 = A1B1. Из равенства треугольников ∆ABD и ∆A1B1D1 следует равенство углов: A = А1.
Так как по условию АВ = А1В1, АС = А1С1, а A = А1 по доказанному, то треугольники ∆АВС и ∆А1В1С1 равны по первому признаку.
ч.т.д.
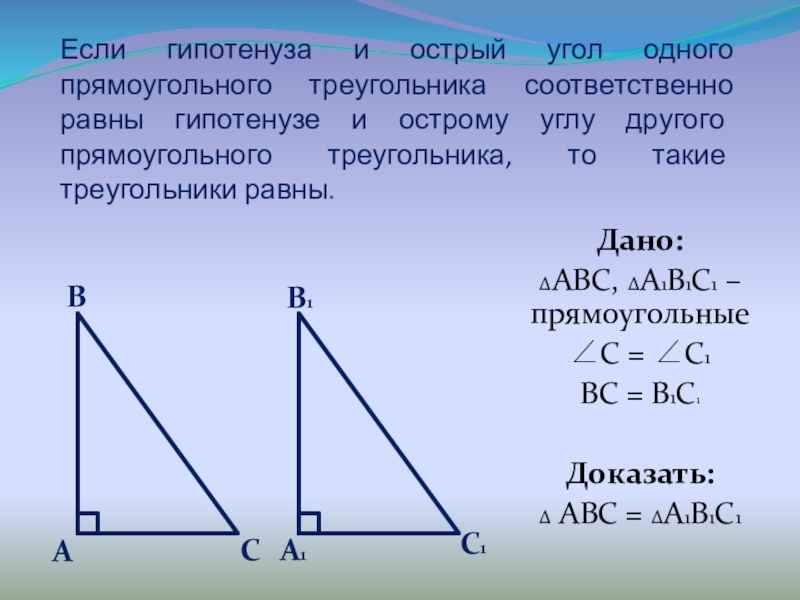
Слайд 13Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе
и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Дано:
ΔABC, ΔA1B1C1 – прямоугольные
C = C1
BC = B1C1
Доказать:
Δ ABC = ΔA1B1C1
Слайд 14Доказательство:
1) Так как ∆ABC и ∆A1B1C1- прямоугольные, то
B = 90° -
С
B1 = 90° - С1 B = B1
С = С1 (по условию)
2) Рассмотрим ∆ABC и ∆A1B1C1 :
B = B1
С = С1 (по условию) ∆ABC = ∆A1B1C1
ВС = В1С1 (по условию) (по II признаку)
ч.т.д.
B1 = 90° - С1 B = B1
С = С1 (по условию)
2) Рассмотрим ∆ABC и ∆A1B1C1 :
B = B1
С = С1 (по условию) ∆ABC = ∆A1B1C1
ВС = В1С1 (по условию) (по II признаку)
ч.т.д.
