- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Признаки равенства треугольников ( 7 класс)
Содержание
- 1. Презентация по геометрии на тему Признаки равенства треугольников ( 7 класс)
- 2. Первый признак равенства треугольниковТеорема: Если две стороны
- 3. ДоказательствоРассмотрим треугольники АВС и А1В1С1, у которых
- 4. ДоказательствоМысленно наложим треугольник АВС на треугольник А1В1С1
- 5. ДоказательствоСледовательно, совместятся стороны ВС и В1С1. Итак, треугольники полностью совместятся, поэтому они равны. Теорема доказана.
- 6. Второй признак равенства треугольниковТеорема: Если сторона и
- 7. ДоказательствоРассмотрим треугольники АВС и А1В1С1, у которых
- 8. ДоказательствоМысленно наложим треугольник АВС так, чтобы вершина
- 9. Третий признак равенства треугольниковТеорема: Если три стороны
- 10. ДоказательствоРассмотрим треугольники АВС и А1В1С1, у которых
- 11. ДоказательствоПриложим треугольник АВС к треугольнику А1В1С1 так,
- 12. ДоказательствоЗначит, 1 = 2 и 3 =
Первый признак равенства треугольниковТеорема: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Слайд 2Первый признак равенства треугольников
Теорема: Если две стороны и угол между ними
одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
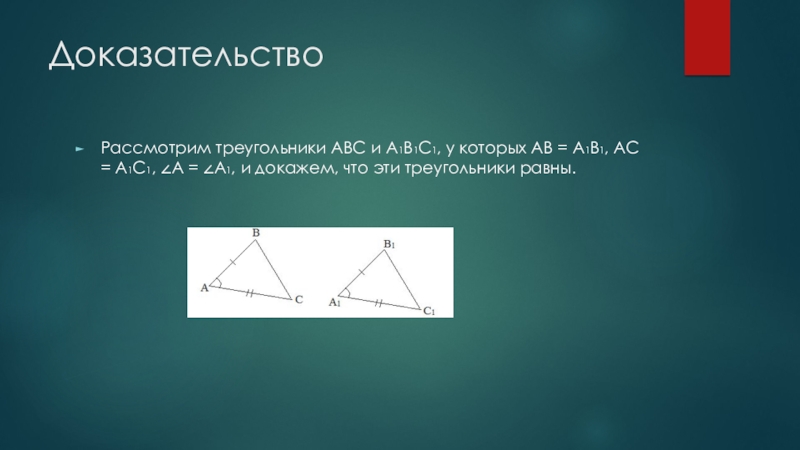
Слайд 3Доказательство
Рассмотрим треугольники АВС и А1В1С1, у которых АВ = А1В1, АС
= А1С1, A = A1, и докажем, что эти треугольники равны.
Слайд 4Доказательство
Мысленно наложим треугольник АВС на треугольник А1В1С1 так, чтобы вершина А
совместилась с вершиной А1, а стороны АВ и АС наложились на лучи А1В1 и А1С1. Это можно сделать, так как углы А и А1 равны.
Поскольку АВ = А1В1 и АС = А1С1, то сторона АВ совместятся со стороной А1В1, а сторона АС совместится со стороной А1С1, в частности совместятся точки В и В1, С и С1.
Поскольку АВ = А1В1 и АС = А1С1, то сторона АВ совместятся со стороной А1В1, а сторона АС совместится со стороной А1С1, в частности совместятся точки В и В1, С и С1.
Слайд 5Доказательство
Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники полностью совместятся, поэтому
они равны. Теорема доказана.
Слайд 6Второй признак равенства треугольников
Теорема: Если сторона и два прилежащих к ней
угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
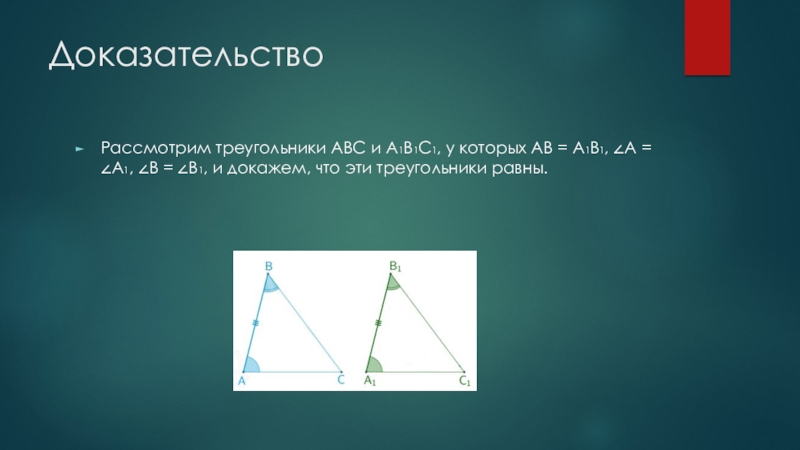
Слайд 7Доказательство
Рассмотрим треугольники АВС и А1В1С1, у которых АВ = А1В1, A
= A1, В = В1, и докажем, что эти треугольники равны.
Слайд 8Доказательство
Мысленно наложим треугольник АВС так, чтобы вершина А совместилась с вершиной
А1, сторона АВ – с равной ей стороной А1В1, а вершина С и С1 оказались по одну сторону от прямой А1В1.
Так как A = A1 и В= В1, то сторона АС наложится на луч А1С1, а сторона ВС – на луч В1С1. Поэтому вершина – С общая точка сторон АС и ВС – совместится с общей точкой лучей А1С1 и В1С1, т.е. с точкой С1.
Из этого следует, что стороны АС и ВС совместятся соответственно со сторонами А1С1 и В1С1. Итак, треугольники полностью совместятся, следовательно, они равны. Теорема доказана.
Так как A = A1 и В= В1, то сторона АС наложится на луч А1С1, а сторона ВС – на луч В1С1. Поэтому вершина – С общая точка сторон АС и ВС – совместится с общей точкой лучей А1С1 и В1С1, т.е. с точкой С1.
Из этого следует, что стороны АС и ВС совместятся соответственно со сторонами А1С1 и В1С1. Итак, треугольники полностью совместятся, следовательно, они равны. Теорема доказана.
Слайд 9Третий признак равенства треугольников
Теорема: Если три стороны одного треугольника соответственно равны
трем сторонам другого треугольника, то такие треугольники равны.
Слайд 10Доказательство
Рассмотрим треугольники АВС и А1В1С1, у которых АВ = А1В1, ВС
= В1С1, АС = А1С1, и докажем, что эти треугольники равны.
Слайд 11Доказательство
Приложим треугольник АВС к треугольнику А1В1С1 так, чтобы вершины А и
А1, В и В1 совместились, а вершины С и С1 оказались по разные стороны от прямой А1В1. Проведем отрезок СС1.
Если он пересекает отрезок А1В1, то получим два равнобедренных треугольника: А1С1С и В1С1С.
Если он пересекает отрезок А1В1, то получим два равнобедренных треугольника: А1С1С и В1С1С.
Слайд 12Доказательство
Значит, 1 = 2 и 3 = 4, и следовательно, С
= С1. Итак, АС = А1С1, ВС = В1С1 и С = С1, поэтому треугольники АВС и А1В1С1 равны по первому признаку равенства треугольников. Теорема доказана.