- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Признаки параллельности прямых (7 класс)
Содержание
- 1. Презентация по геометрии на тему Признаки параллельности прямых (7 класс)
- 2. Две прямые на плоскости называются параллельными,если они не пересекаются.ОпределениеПараллельность прямых a и b обозначают так: a║b.cab
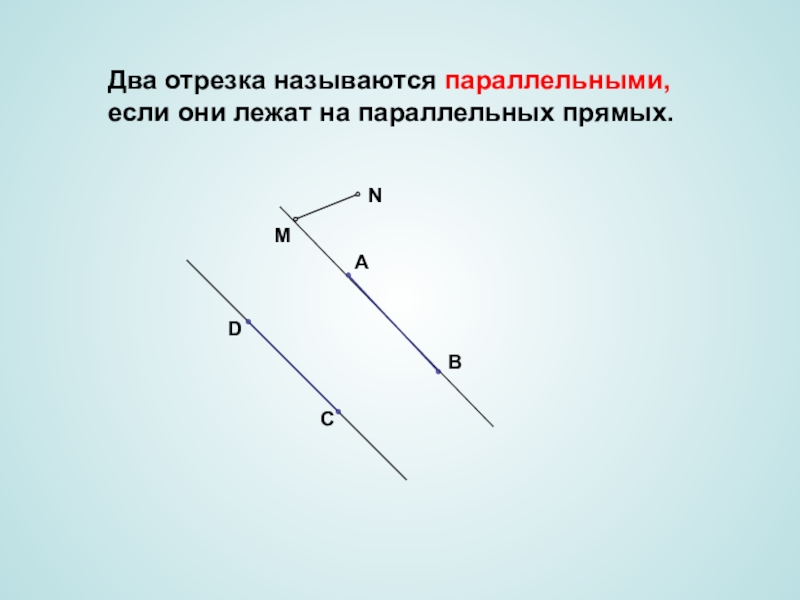
- 3. Два отрезка называются параллельными, если они лежат на параллельных прямых. CDMNAB
- 4. 56871243abНакрест лежащие углы: 3 и 5, 4
- 5. Теорема.Если при пересечение двух прямых секущей накрест
- 6. Рассмотрим особо пункт 6:ے3= ے4, поэтому точки
- 7. Теорема. Если при пересечении двух прямых секущейсоответственные
- 8. III признак.Теорема.Если при пересечение двух прямых секущейсумма
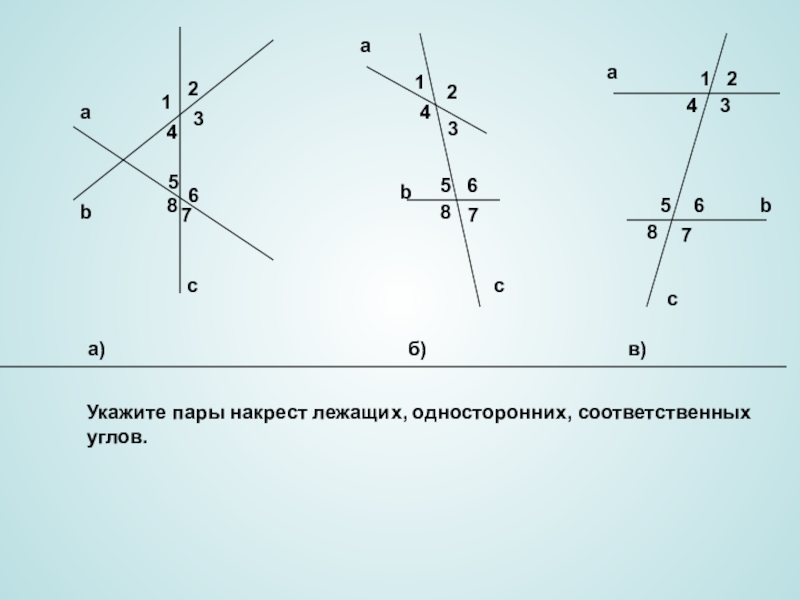
- 9. abc12435687a)б)в)Укажите пары накрест лежащих, односторонних, соответственныхуглов. 12435687acba1243b5687c
- 10. Слайд 10
Слайд 2
Две прямые на плоскости называются параллельными,
если они не пересекаются.
Определение
Параллельность прямых a
c
a
b
Слайд 45
6
8
7
1
2
4
3
a
b
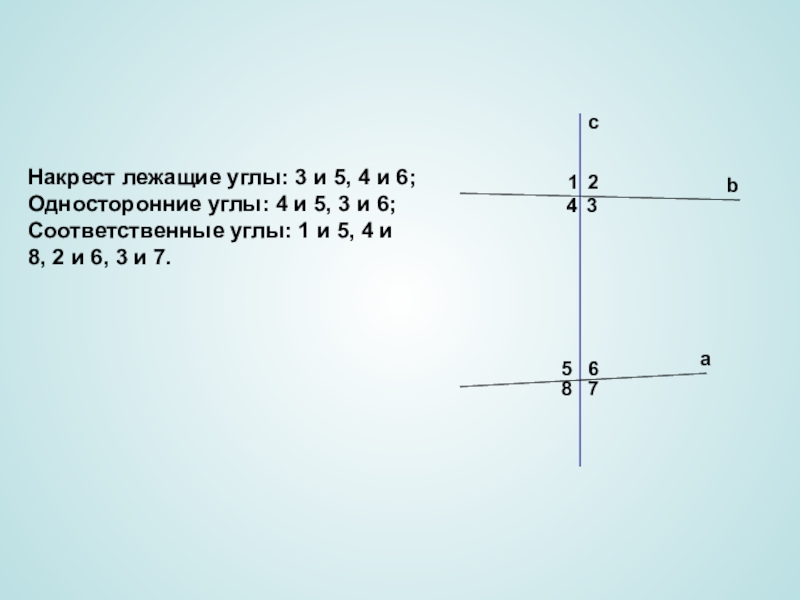
Накрест лежащие углы: 3 и 5, 4 и 6;
Односторонние углы: 4
Соответственные углы: 1 и 5, 4 и
8, 2 и 6, 3 и 7.
c
Слайд 5Теорема.
Если при пересечение двух прямых секущей накрест лежащие углы равны, то
a
b
O
c
H
A
1
2
H1
6
4
5
3
B
Дано: a ∩ с = A, b ∩ c = B,
ے1 и ے2 накрест лежащие,
ے1 = ے2.
Доказать: a ║ b.
Доказательство:
I. Если ے1 = ے2= 90°, то a AB
И b AB, тогда a ║ b.
װ. Пусть углы 1 и 2 не прямые.
1. Разделим отрезок AB пополам, получим O.
2. Проведем OH a.
3. На прямой b от точки B отложим BH1 = AH и
Проведем отрезок OH1.
4. Треугольник OHA = треугольнику OH1B по
двум сторонам и углу между ними (OA = OB,
AH = BH1, ے1= ے2).
5. ے3= ے4, ے5 = ے6 = 90°.
6. ے3= ے4, поэтому точки H1, O, H лежат на одной
прямой.
7. a HH1 и b HH1, значит, a ║ b.
Теорема доказана.
I признак
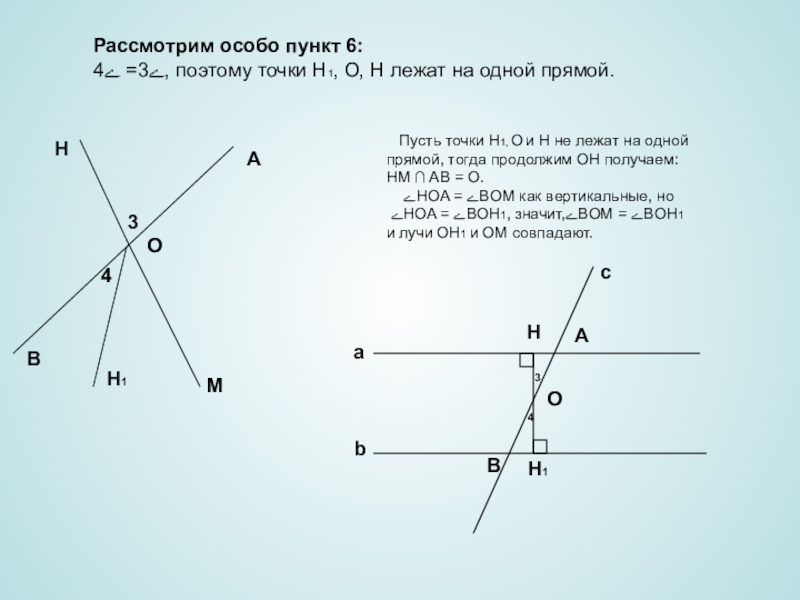
Слайд 6Рассмотрим особо пункт 6:
ے3= ے4, поэтому точки H1, O, H лежат
O
3
4
M
H1
B
H
A
Пусть точки H1, O и H не лежат на одной
прямой, тогда продолжим OH получаем:
HM ∩ AB = O.
ےHOA = ےBOM как вертикальные, но
ےHOA = ےBOH1, значит,ےBOM = ےBOH1
и лучи OH1 и OM совпадают.
c
a
b
H
H1
B
A
O
3
4
Слайд 7Теорема.
Если при пересечении двух прямых секущей
соответственные углы равны, то прямые
параллельны.
װ
b
a
c
2
3
1
Дано: a ∩ c, b ∩ c,
ے1 и ے2 соответственные,
ے1 = ے2.
Доказать: a ║ b.
Доказательство:
ے 2= ے3 как вертикальные.
ے2 = ے1 по условию.
Значит, ے1 = ے3.
Но ے1 и ے3 накрест лежащие,
поэтому a ║ b.
Теорема доказана.
Слайд 8
III признак.
Теорема.
Если при пересечение двух прямых секущей
сумма односторонних углов равна 180°,
прямые параллельны.
3
4
b
a
c
1
Дано: a ∩ c, b ∩ c,
ے1 и ے4 – односторонние,
ے1 + ے4 = 180°.
Доказать: a ║ b.
Доказательство:
1. ے3 и ے4 – смежные, значит,
ے3 + ے4 = 180°.
2. ے1 + ے4 = 180° по условию.
3. Отсюда ے1 = ے3.
4. Но ے1 и ے3 накрест лежащие,
поэтому a ║ b.
Теорема доказана.
Слайд 9a
b
c
1
2
4
3
5
6
8
7
a)
б)
в)
Укажите пары накрест лежащих, односторонних, соответственных
углов.
1
2
4
3
5
6
8
7
a
c
b
a
1
2
4
3
b
5
6
8
7
c
