свойства.
(Обобщающий урок)
7 класс
Учитель математики ГБПОУ МГТТиП, г. Москвы
Руденко Галина Михайловна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему: Признаки равенства треугольников (7 класс)
Содержание
- 1. Презентация по геометрии на тему: Признаки равенства треугольников (7 класс)
- 2. Слайд 2
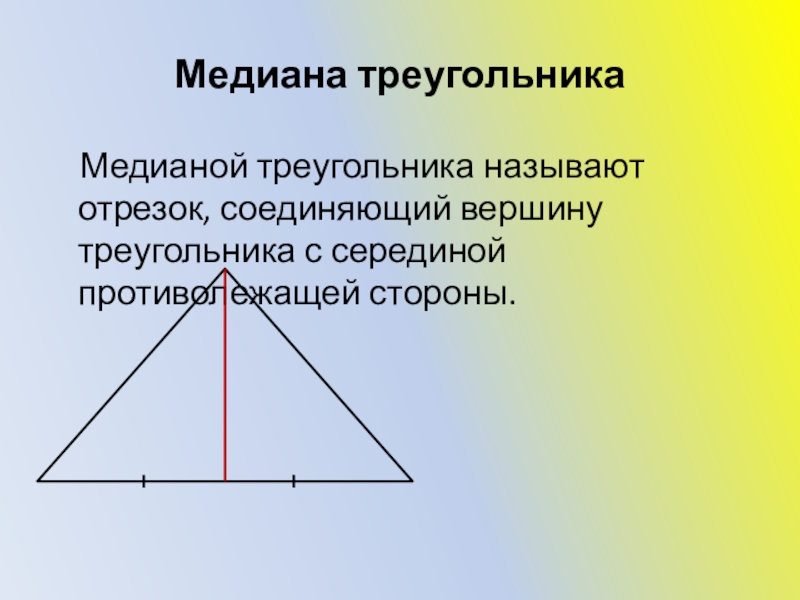
- 3. Медиана треугольника Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
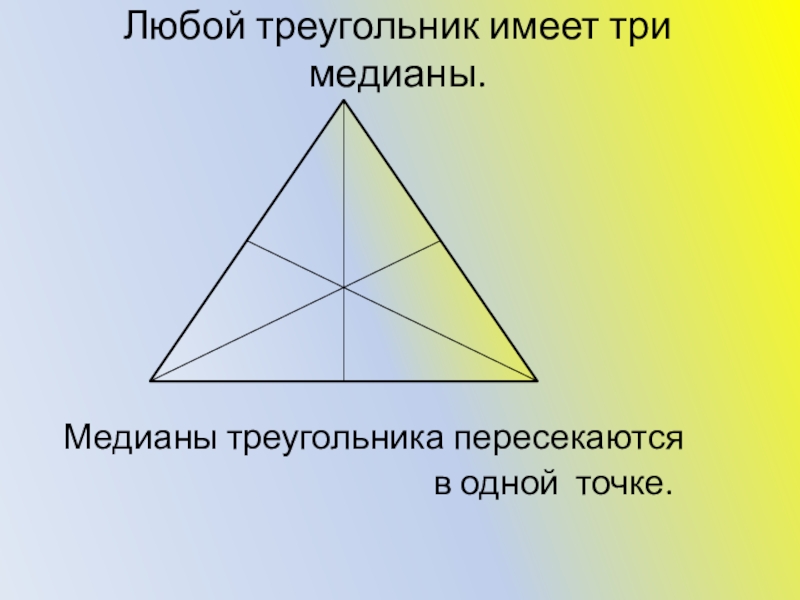
- 4. Любой треугольник имеет три медианы. Медианы
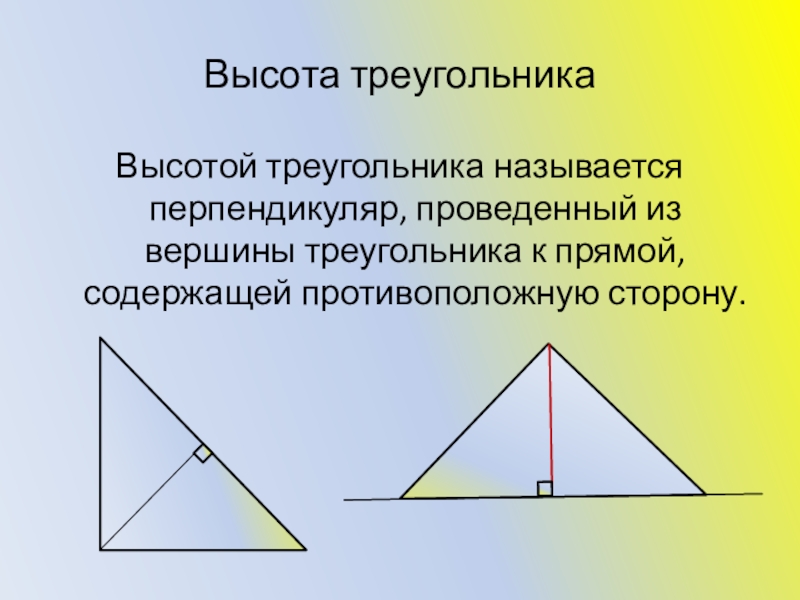
- 5. Высота треугольникаВысотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
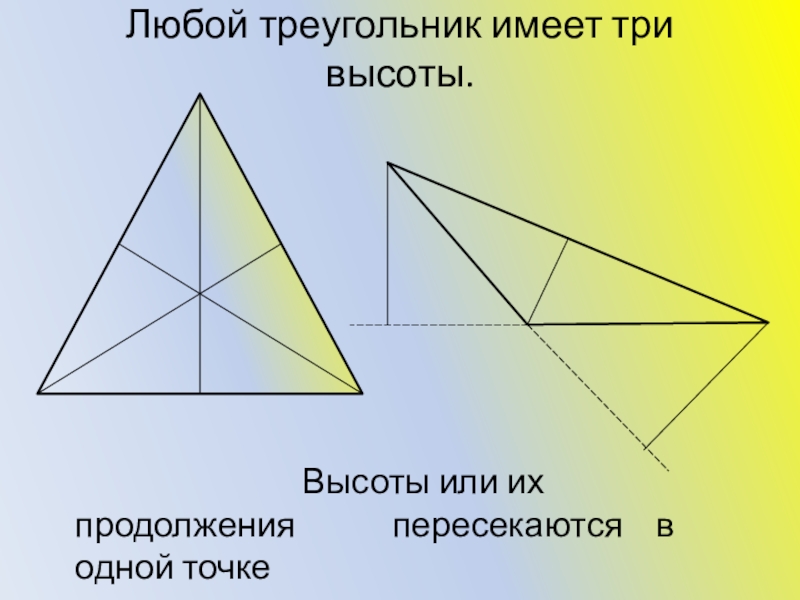
- 6. Любой треугольник имеет три высоты.
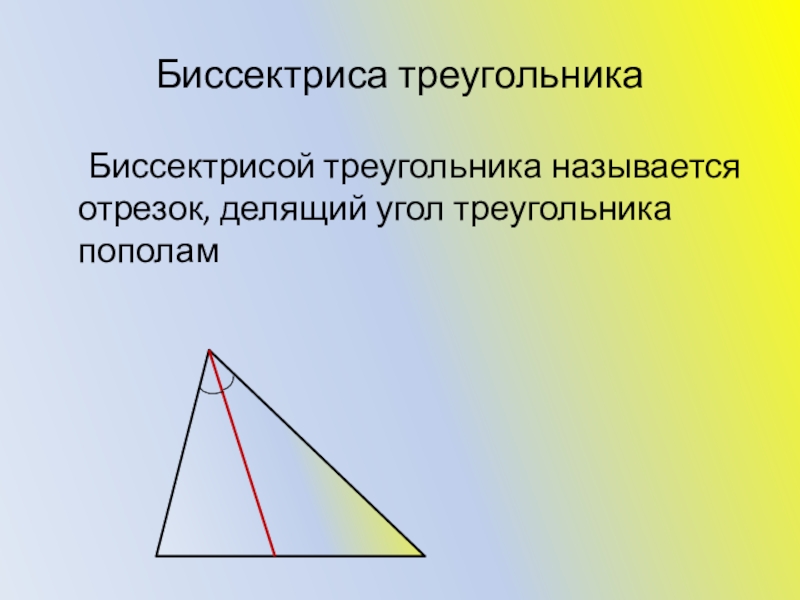
- 7. Биссектриса треугольника Биссектрисой треугольника называется отрезок, делящий угол треугольника пополам
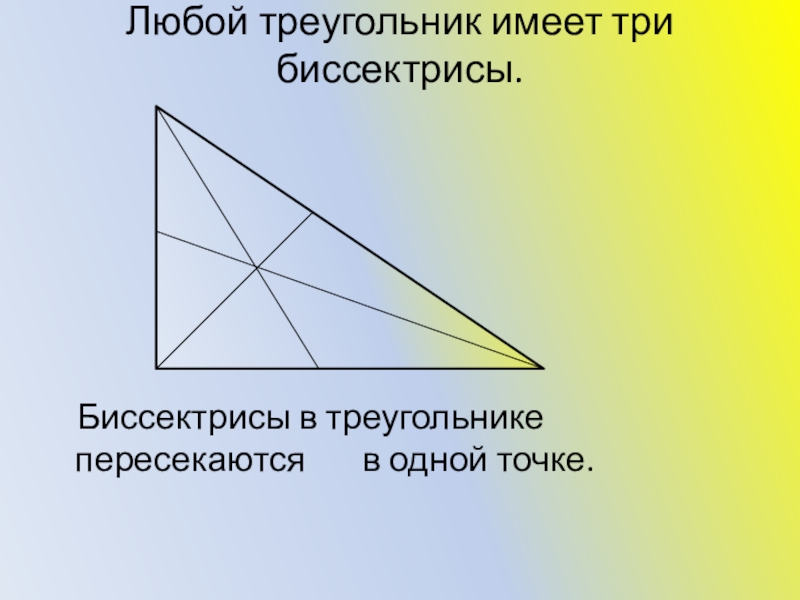
- 8. Любой треугольник имеет три биссектрисы.
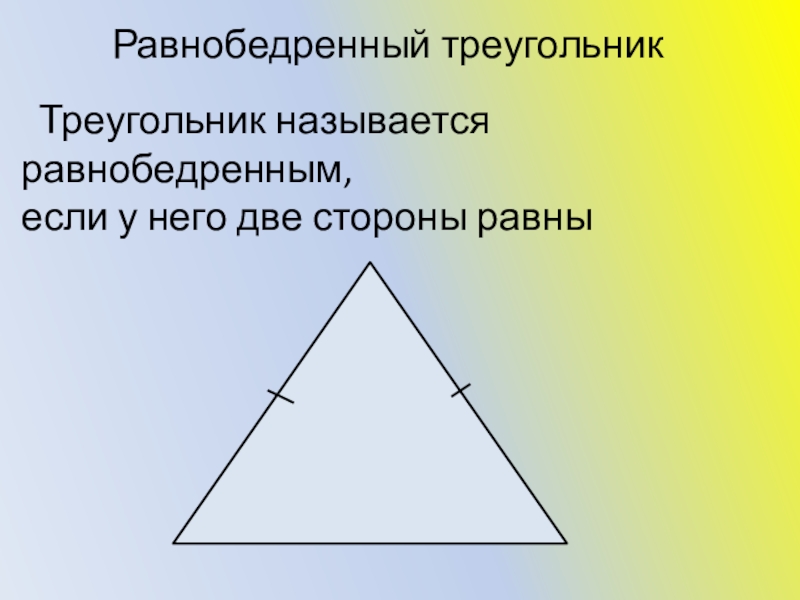
- 9. Треугольник называется равнобедренным, если у него
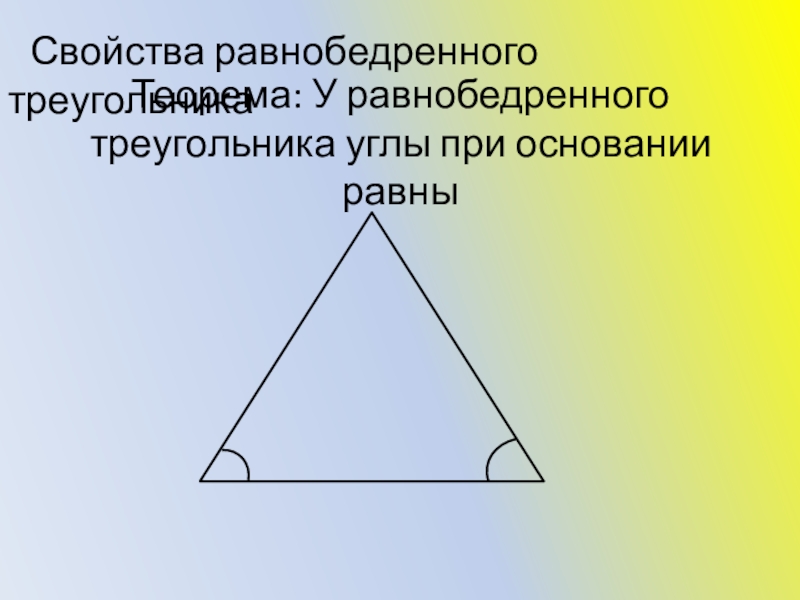
- 10. Теорема: У равнобедренного треугольника углы при основании равны Свойства равнобедренного треугольника
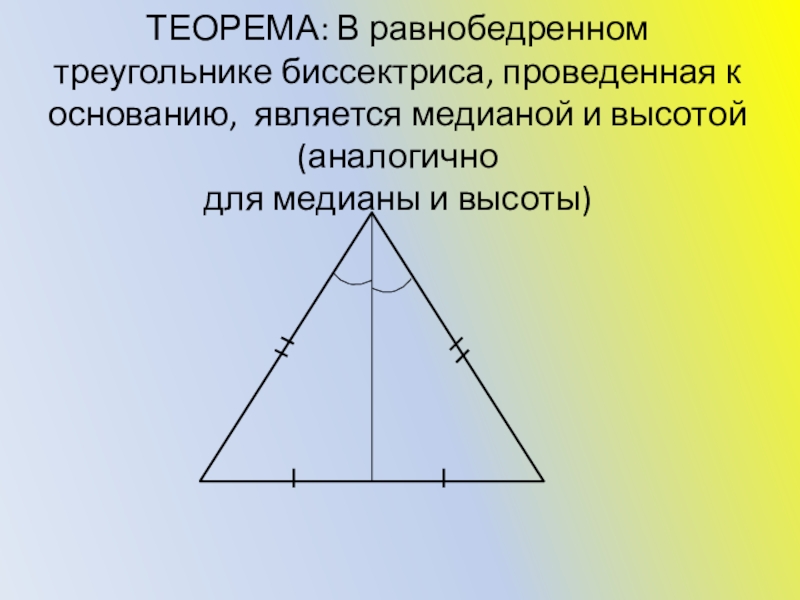
- 11. ТЕОРЕМА: В равнобедренном треугольнике биссектриса, проведенная к
- 12. Задача 1:В равнобедренном треугольнике основание на 30
- 13. Слайд 13
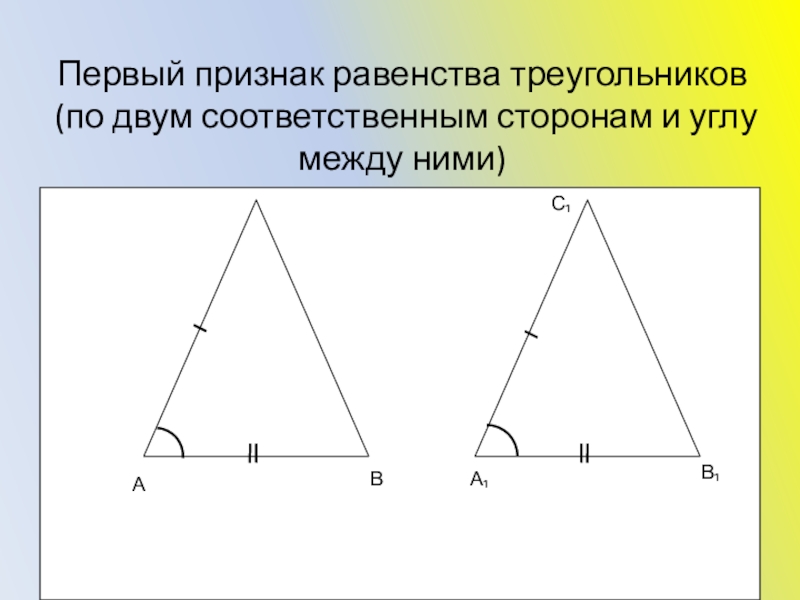
- 14. Первый признак равенства треугольников (по двум соответственным сторонам и углу между ними)АВА₁В₁С₁
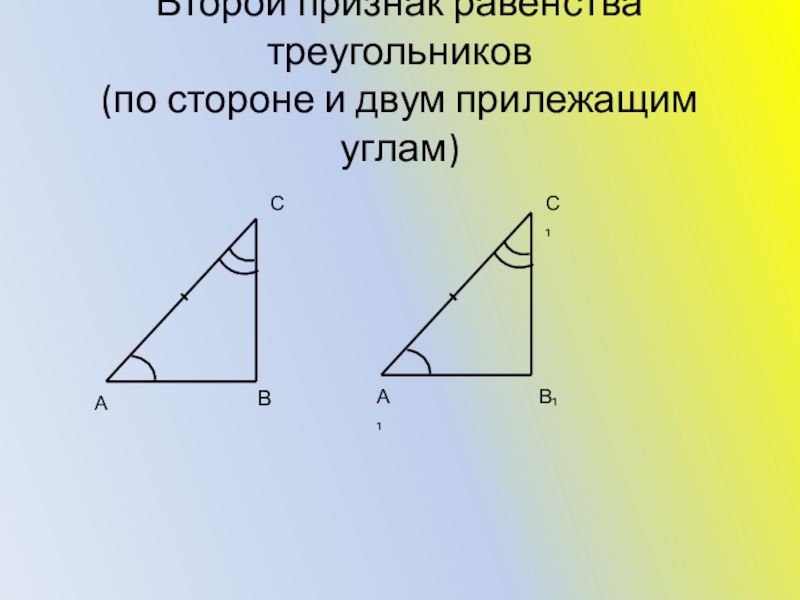
- 15. Второй признак равенства треугольников (по стороне и двум прилежащим углам)ВСАА₁В₁С₁
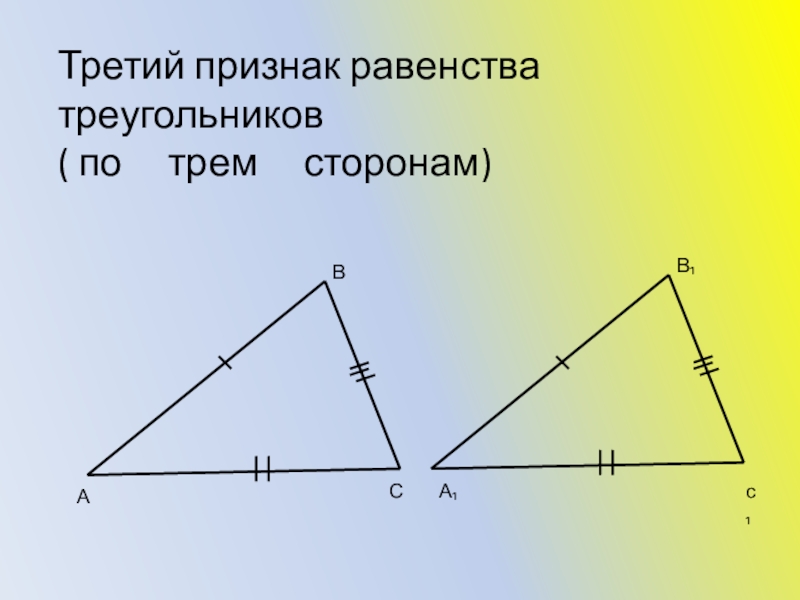
- 16. АВСА₁В₁с₁Третий признак равенства треугольников ( по трем сторонам)
- 17. Задача № 1 Отрезки КМ и LN
- 18. Задача №2 В равнобедренном треугольнике АВС
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
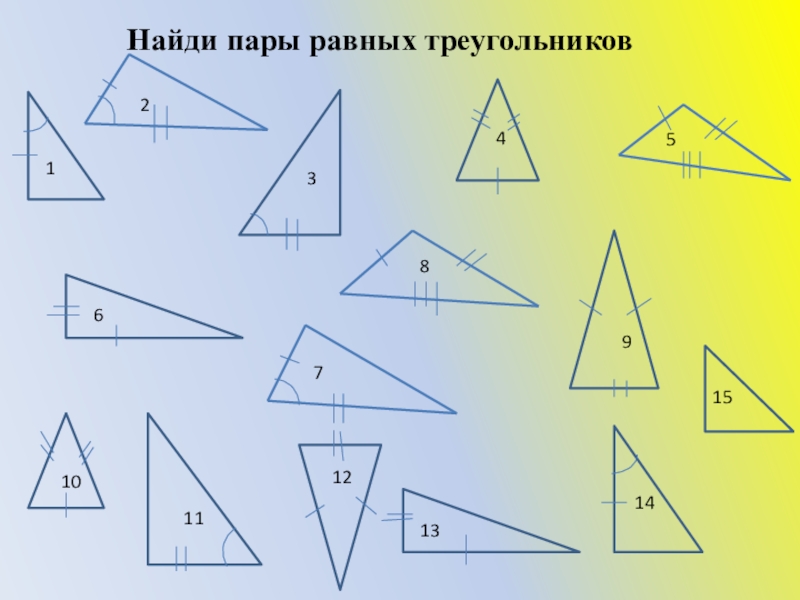
- 22. Найди пары равных треугольников123456789101112131415
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
- 27. Задача № 12 Два
- 28. Задача № 13 Равные отрезки
- 29. Решение задач по готовым чертежам
- 30. ВСАD12Дано: ВD— биссектриса угла АВС,
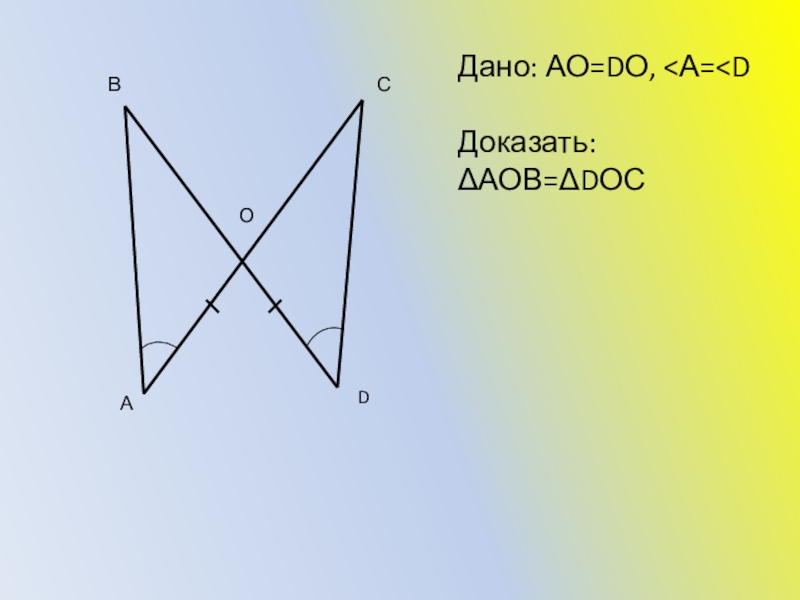
- 31. ВСАDДано: АО=DО,
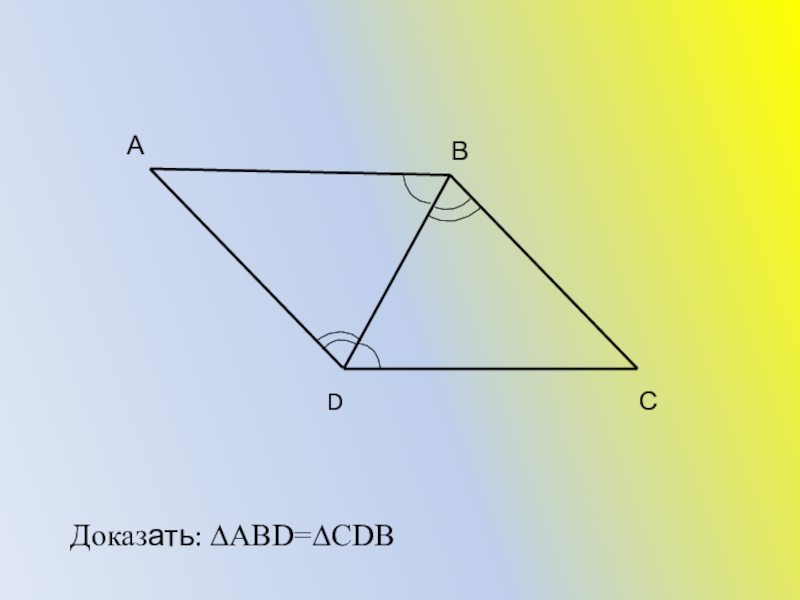
- 32. АВDСДоказать: ∆АВD=∆CDВ
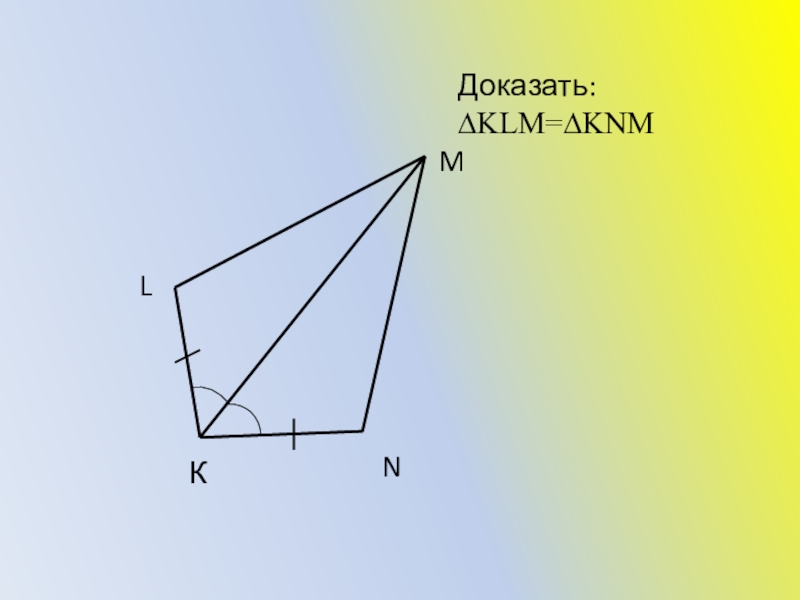
- 33. Доказать: ∆KLM=∆KNMКLMN
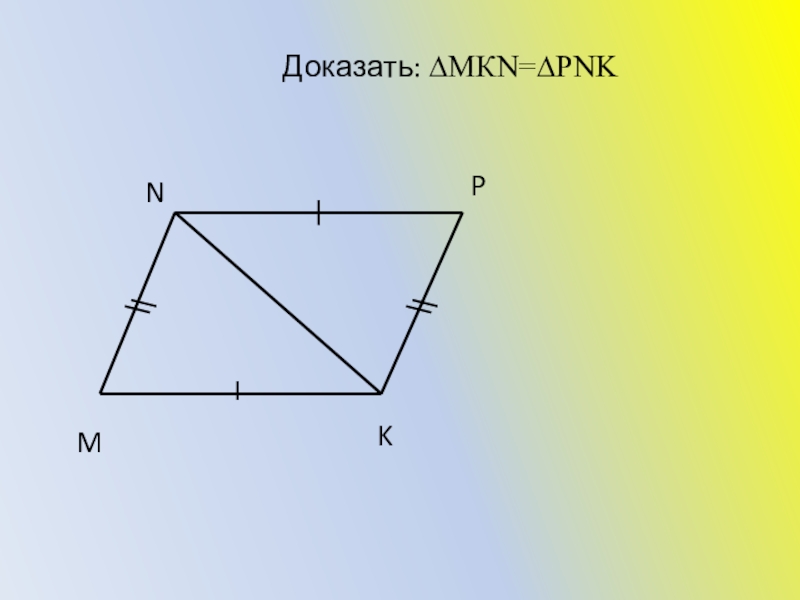
- 34. MKPNДоказать: ∆МКN=∆PNK
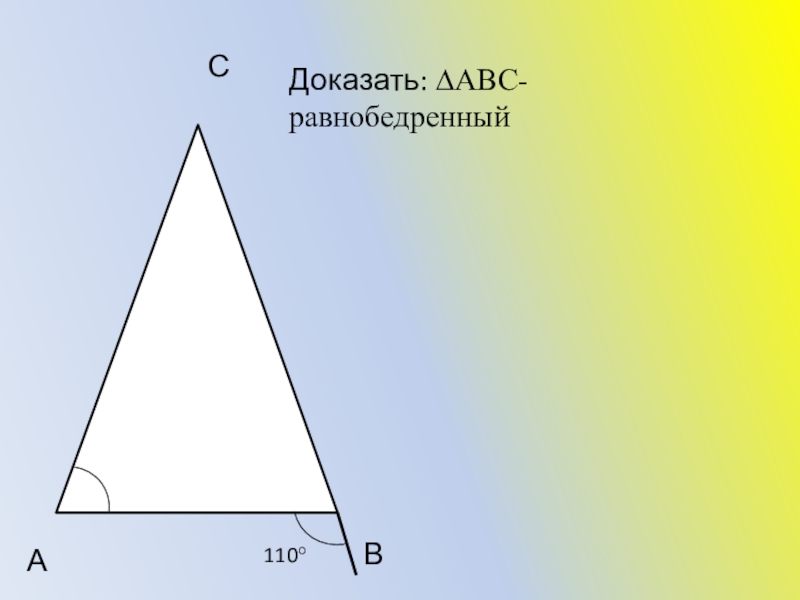
- 35. АВСДоказать: ∆АВС- равнобедренный110°
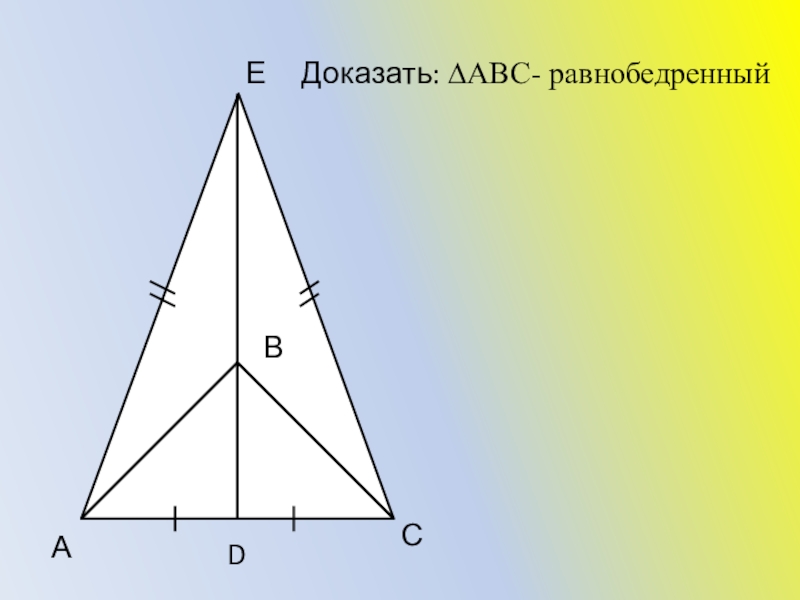
- 36. АСЕВDДоказать: ∆АВС- равнобедренный
- 37. аМРОКН110⁰Дано: Точки М и Р лежат по
- 38. Дано: ΔАВС— равнобедренный, СD – медиана, т.
- 39. Доказать, что если медиана
- 40. Слайд 40
Перпендикуляр к прямой Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если он образует прямой угол с прямой а.АНа Теорема: Из точки, не
Слайд 1Признаки равенства треугольников. Высота, медиана, биссектриса треугольника. Равнобедренный треугольник и его
Слайд 2 Перпендикуляр
к прямой
Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если он образует прямой угол с прямой а.
А
Н
а
Теорема: Из точки, не лежащей на прямой , можно провести перпендикуляр к этой прямой, и притом только один.
Слайд 3Медиана треугольника
Медианой треугольника называют отрезок, соединяющий вершину треугольника с
серединой противолежащей стороны.
Слайд 5Высота треугольника
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой,
содержащей противоположную сторону.
Слайд 7Биссектриса треугольника
Биссектрисой треугольника называется отрезок, делящий угол треугольника
пополам
Слайд 8Любой треугольник имеет три биссектрисы.
Биссектрисы в треугольнике пересекаются
в одной точке.
Слайд 9 Треугольник называется равнобедренным,
если у него две стороны равны
Равнобедренный треугольник
Слайд 10Теорема: У равнобедренного треугольника углы при основании равны
Свойства
равнобедренного треугольника
Слайд 11ТЕОРЕМА: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и
высотой (аналогично
для медианы и высоты)
Слайд 12Задача 1:
В равнобедренном треугольнике основание на 30 см меньше боковой стороны,
а периметр равен 150 см. Найти стороны треугольника.
Задача 2:
В равнобедренном треугольнике боковая сторона в 3 раза больше основания, а периметр равен 49. Найти стороны треугольника.
Задача 3:
В равнобедренном треугольнике угол при вершине В равен 70˚. Найдите угол АВМ, если из вершины В к основанию АС проведена медиана ВМ.
Слайд 13
Равные треугольники
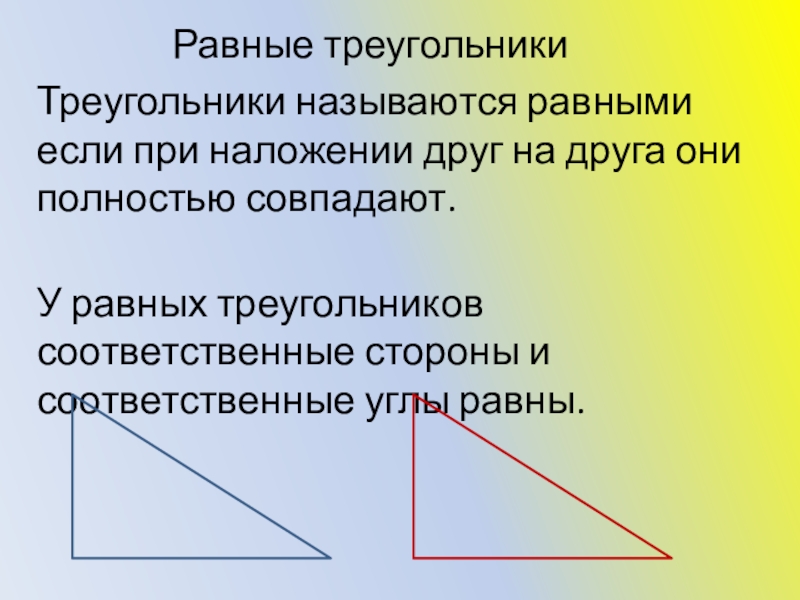
Треугольники называются равными если при наложении друг на друга они полностью совпадают.
У равных треугольников соответственные стороны и соответственные углы равны.
Слайд 14 Первый признак равенства треугольников (по двум соответственным сторонам и углу между
ними)
А
В
А₁
В₁
С₁
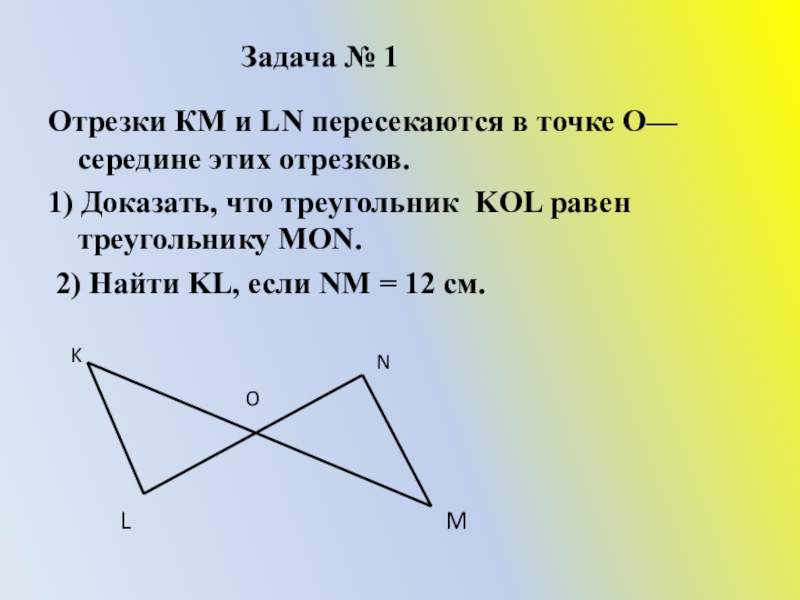
Слайд 17Задача № 1
Отрезки КМ и LN пересекаются в точке О—середине этих
отрезков.
1) Доказать, что треугольник KOL равен треугольнику MON.
2) Найти KL, если NM = 12 см.
1) Доказать, что треугольник KOL равен треугольнику MON.
2) Найти KL, если NM = 12 см.
N
M
K
L
O
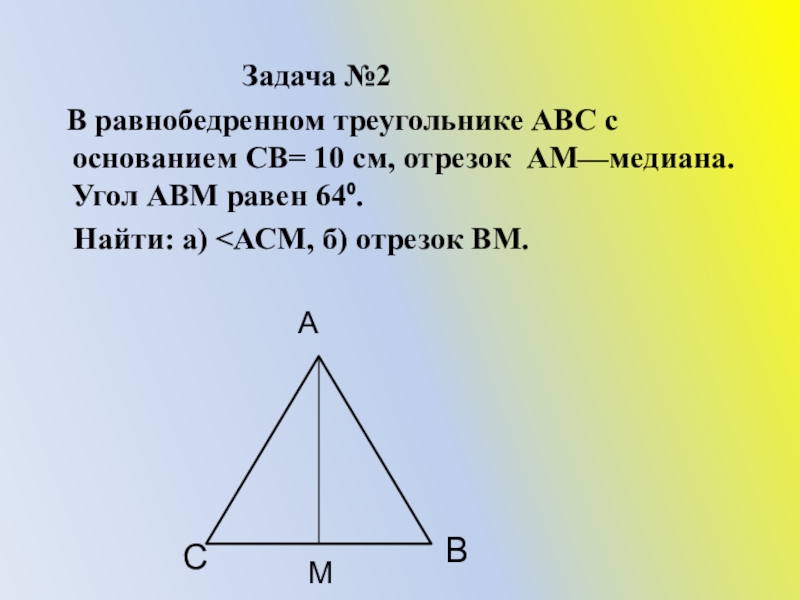
Слайд 18Задача №2
В равнобедренном треугольнике АВС с основанием СВ= 10
см, отрезок АМ—медиана. Угол АВМ равен 64⁰.
Найти: а) <АСМ, б) отрезок ВМ.
Найти: а) <АСМ, б) отрезок ВМ.
В
С
М
А
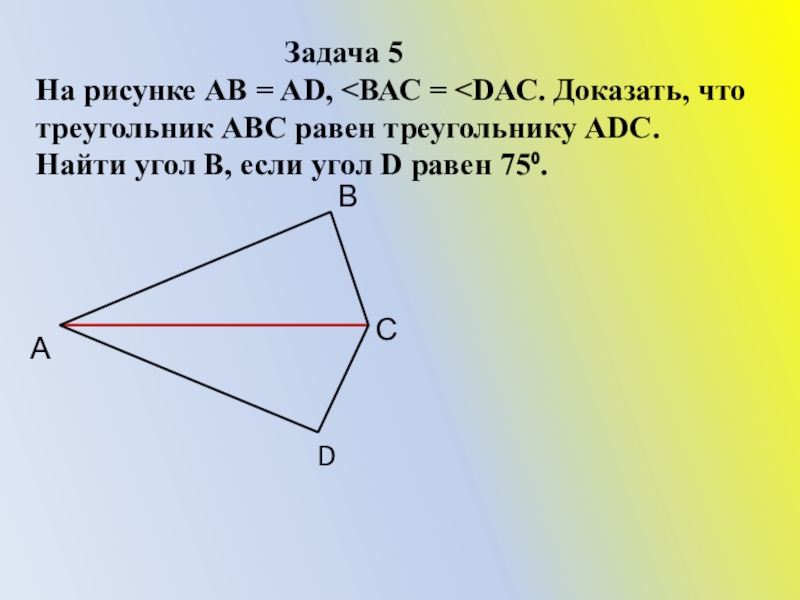
Слайд 19
Задача 3
На рисунке ВС = АD, <ВСА = < DАС.
Доказать, что треугольники АВС и АСD равны. Найти сторону ВА, если сторона СD = 3 см.
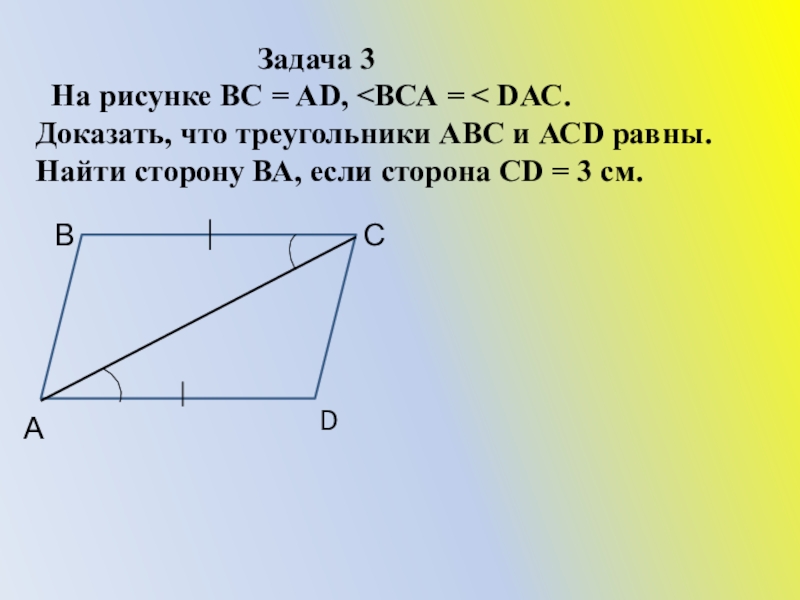
На рисунке ВС = АD, <ВСА = < DАС.
Доказать, что треугольники АВС и АСD равны. Найти сторону ВА, если сторона СD = 3 см.
А
D
В
С
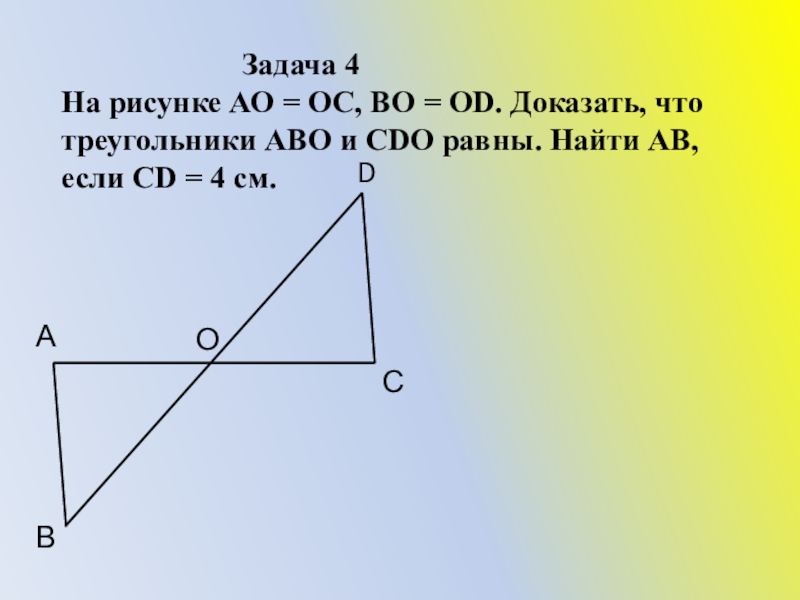
Слайд 20
Задача 4
На рисунке АО = ОС, ВО = ОD. Доказать, что треугольники АВО и CDО равны. Найти АВ, если CD = 4 см.
На рисунке АО = ОС, ВО = ОD. Доказать, что треугольники АВО и CDО равны. Найти АВ, если CD = 4 см.
А
В
С
D
О
Слайд 24
Задача 6
В треугольнике АВС АВ = ВС, ВМ–биссектриса <АВС.
Доказать, что треугольники АВМ и СВМ равны.
Найти угол АВМ, если угол АВС равен 70⁰.
В треугольнике АВС АВ = ВС, ВМ–биссектриса <АВС.
Доказать, что треугольники АВМ и СВМ равны.
Найти угол АВМ, если угол АВС равен 70⁰.
Задача 7
В треугольнике KLM, LS – биссектриса, KL = LM. Доказать, что треугольники KLS и MLS равны.
Найти сторону КМ, если KS = 7,5 см.
Задача 8
В треугольнике OPR OP = PR, PS – биссектриса угла OPR. Доказать, что треугольники OPS и RPS равны. Найти угол OPR, если угол OPS равен 23⁰.
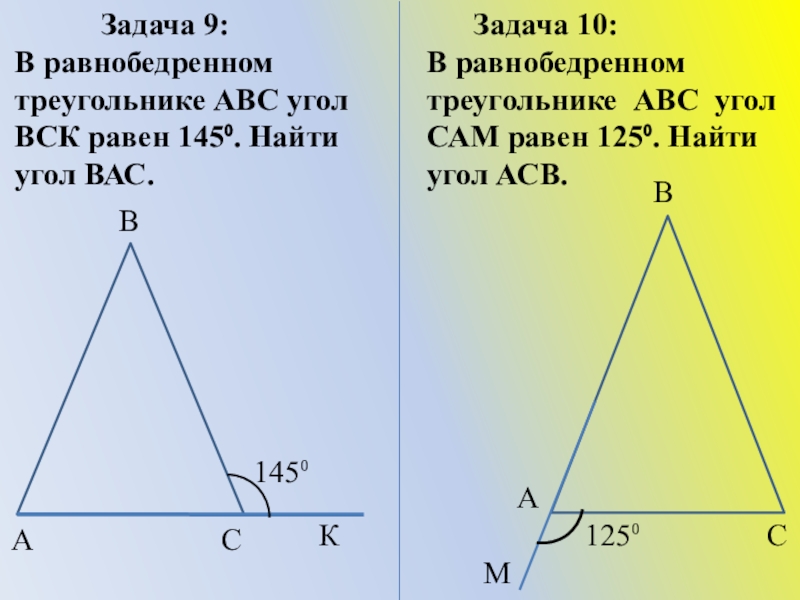
Слайд 25 Задача
9:
В равнобедренном треугольнике АВС угол ВСК равен 145⁰. Найти угол ВАС.
В равнобедренном треугольнике АВС угол ВСК равен 145⁰. Найти угол ВАС.
А
В
С
145⁰
К
Задача 10:
В равнобедренном треугольнике АВС угол САМ равен 125⁰. Найти угол АСВ.
А
С
В
125⁰
М
Слайд 26
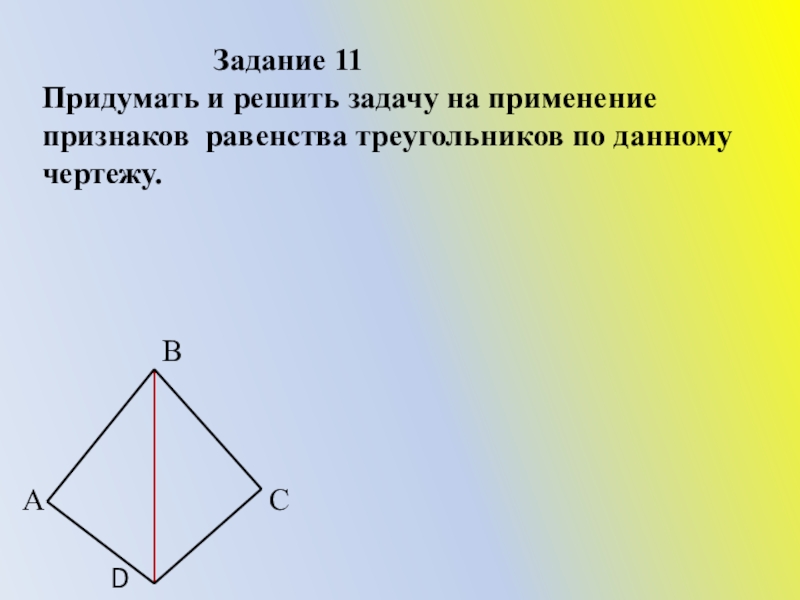
Задание 11
Придумать и решить задачу на применение признаков равенства треугольников по данному чертежу.
А
В
С
D
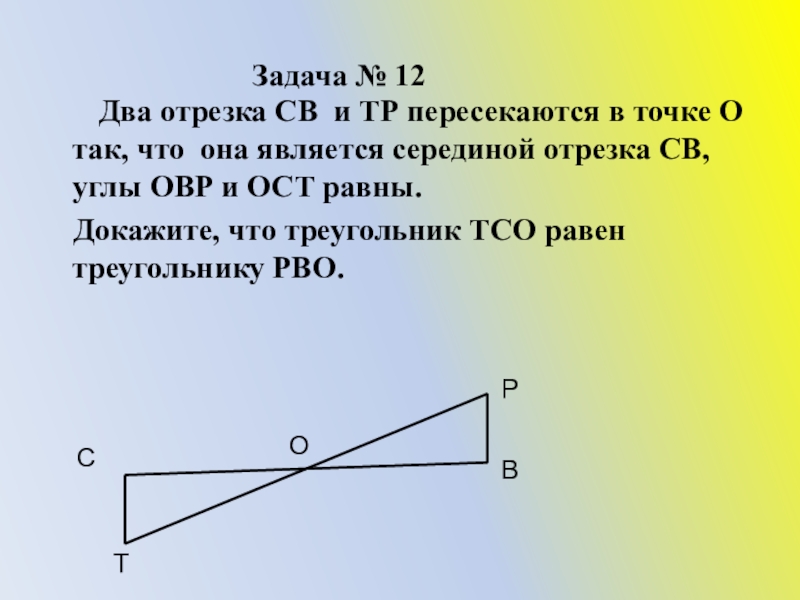
Слайд 27Задача № 12
Два отрезка СВ и ТР
пересекаются в точке О так, что она является серединой отрезка СВ, углы ОВР и ОСТ равны.
Докажите, что треугольник ТСО равен треугольнику РВО.
Докажите, что треугольник ТСО равен треугольнику РВО.
С
В
Р
Т
О
Слайд 28Задача № 13
Равные отрезки АС и ВD пересекаются
в точке О, АВ= СD. Докажите, что углы САD и ВDА равны.
В
В
D
С
А
О
Слайд 37а
М
Р
О
К
Н
110⁰
Дано:
Точки М и Р лежат по одну сторону от прямой
а. Перпендикуляры МН и РК к прямой, равны. Точка О— середина отрезка НК.
1) Доказать, что ∆ОМH= ∆ОРK.
2) Найти <НОМ, если <МОР= 110⁰.
1) Доказать, что ∆ОМH= ∆ОРK.
2) Найти <НОМ, если <МОР= 110⁰.
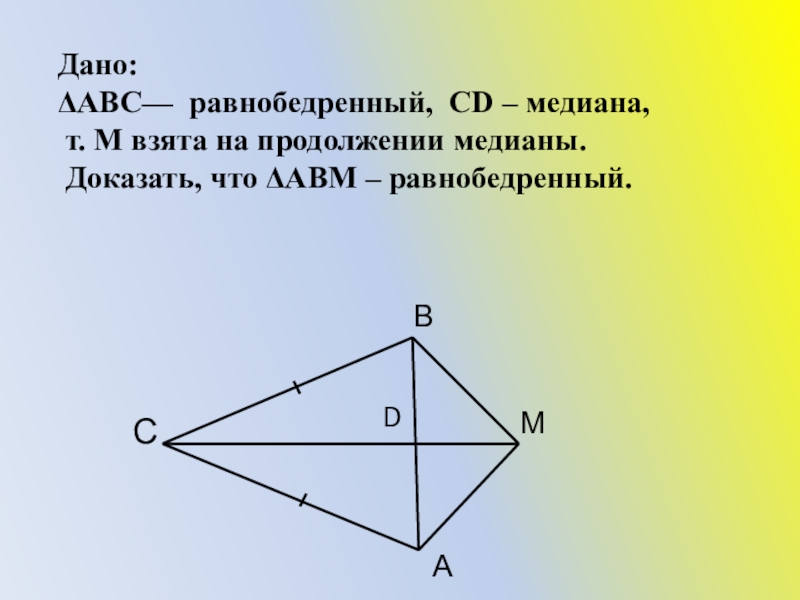
Слайд 38Дано:
ΔАВС— равнобедренный, СD – медиана,
т. М взята на продолжении
медианы.
Доказать, что ΔАВМ – равнобедренный.
Доказать, что ΔАВМ – равнобедренный.
С
D
М
В
А
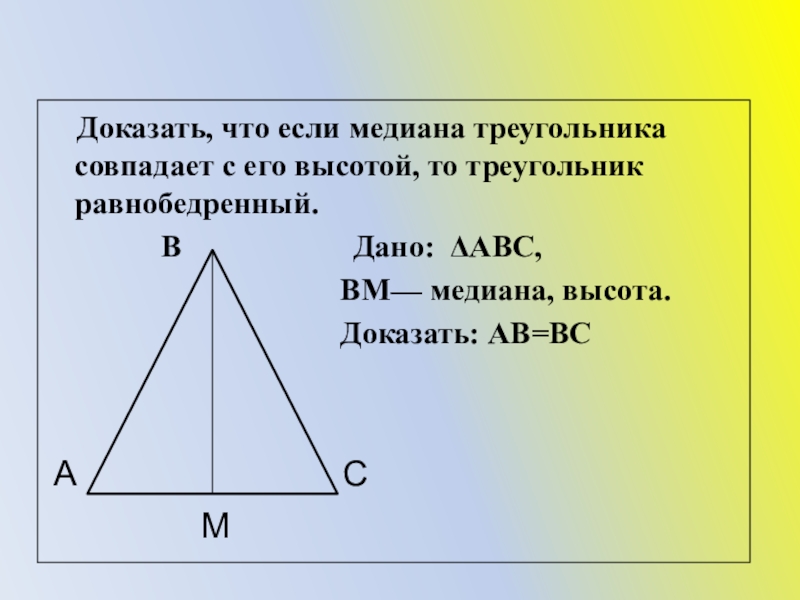
Слайд 39
Доказать, что если медиана треугольника совпадает с его высотой,
то треугольник равнобедренный.
В Дано: ΔАВС,
ВМ— медиана, высота.
Доказать: АВ=ВС
А С
В Дано: ΔАВС,
ВМ— медиана, высота.
Доказать: АВ=ВС
А С
М
