Выполнил:
ученик 10-го класса
Налетов Илья
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему: Признак перпендикулярности прямой и плоскости
Содержание
- 1. Презентация по геометрии на тему: Признак перпендикулярности прямой и плоскости
- 2. αKMLOnlkmИтак, у нас имеется: плоскость α; лежащие
- 3. AαKMLBOnlkmНа прямой а отложим произвольно отложим равные
- 4. AαKMLBOnlkmНа прямой а отложим произвольно отложим равные
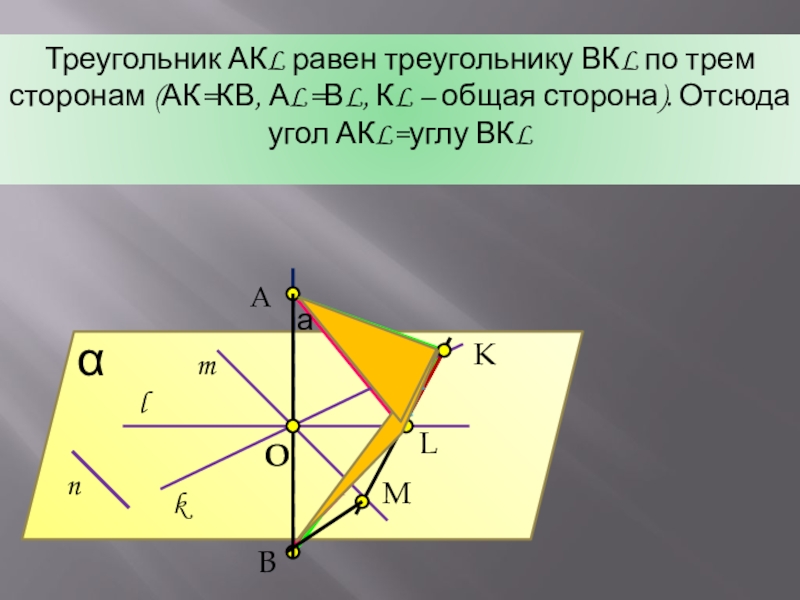
- 5. AαKMLBOnlkmТреугольник АКL равен треугольнику ВКL по трем
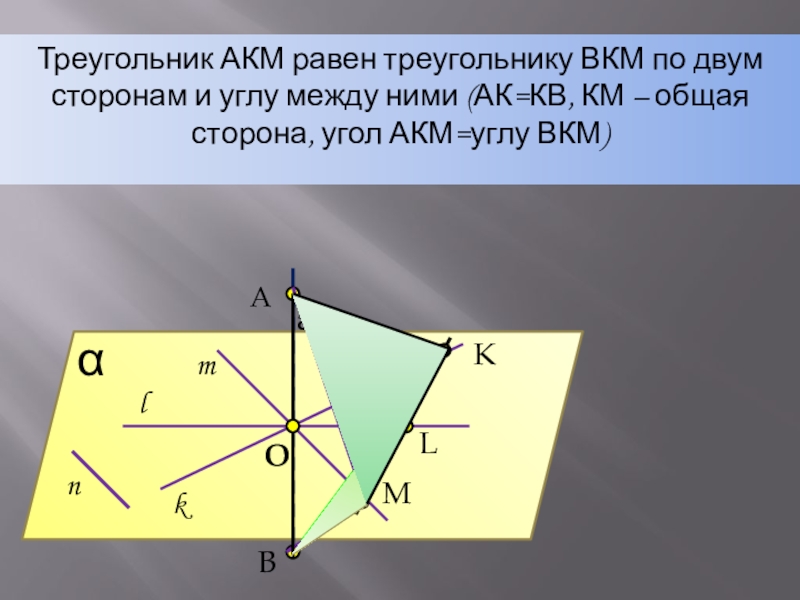
- 6. AαKMLBOnlkmаТреугольник АКМ равен треугольнику ВКМ по двум
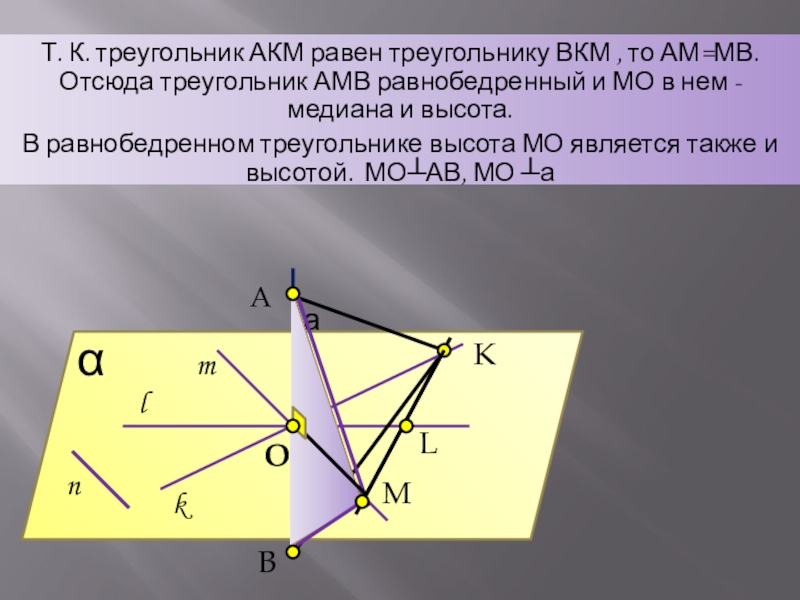
- 7. AαKMLBOnlkmаТ. К. треугольник АКМ равен треугольнику ВКМ
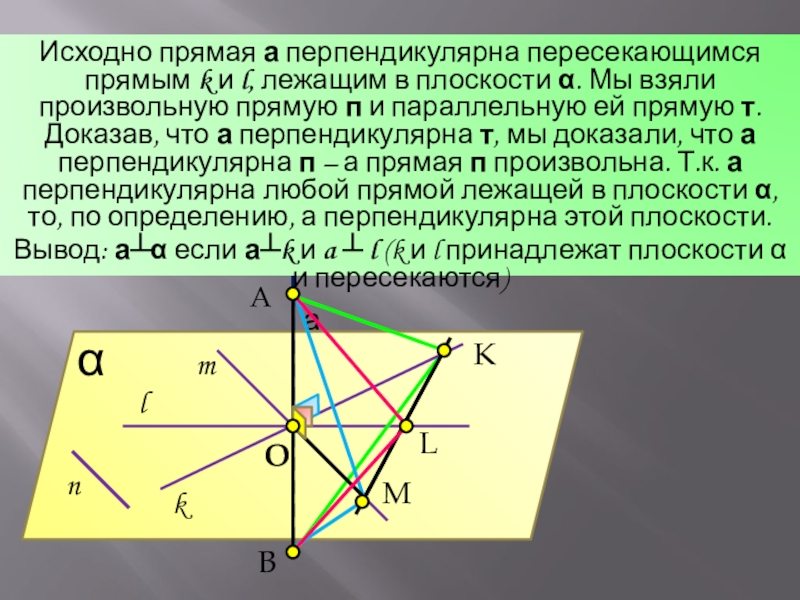
- 8. AαKMLBOnlkmаИсходно прямая а перпендикулярна пересекающимся прямым k
αKMLOnlkmИтак, у нас имеется: плоскость α; лежащие в ней прямые k и l, пересекающиеся в т.О; прямая а, перпендикулярная прямым k и l .Также возьмем на плоскости производную прямую n и проведем прямую m, параллельную прямой
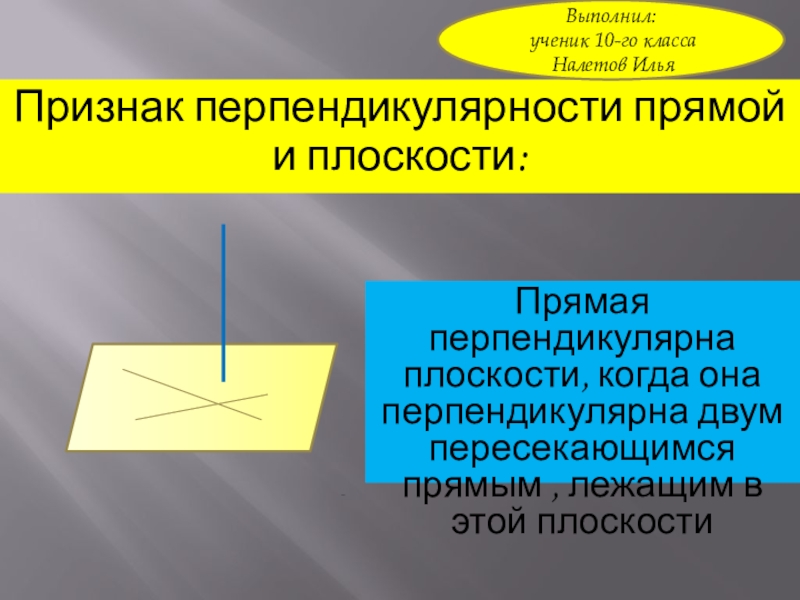
Слайд 1Признак перпендикулярности прямой и плоскости:
Прямая перпендикулярна плоскости, когда она перпендикулярна двум
пересекающимся прямым , лежащим в этой плоскости
Слайд 2α
K
M
L
O
n
l
k
m
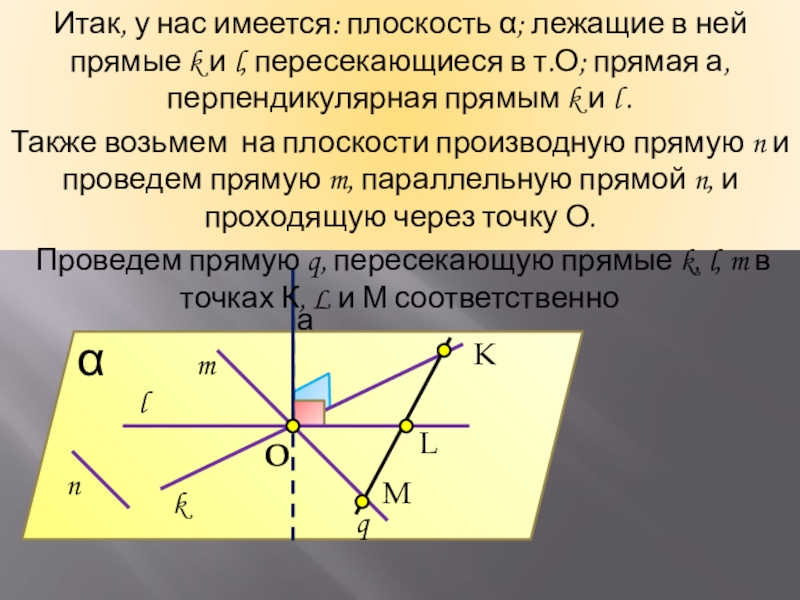
Итак, у нас имеется: плоскость α; лежащие в ней прямые k
и l, пересекающиеся в т.О; прямая а, перпендикулярная прямым k и l .
Также возьмем на плоскости производную прямую n и проведем прямую m, параллельную прямой n, и проходящую через точку О.
Проведем прямую q, пересекающую прямые k, l, m в точках К, L и М соответственно
Также возьмем на плоскости производную прямую n и проведем прямую m, параллельную прямой n, и проходящую через точку О.
Проведем прямую q, пересекающую прямые k, l, m в точках К, L и М соответственно
а
q
Слайд 3A
α
K
M
L
B
O
n
l
k
m
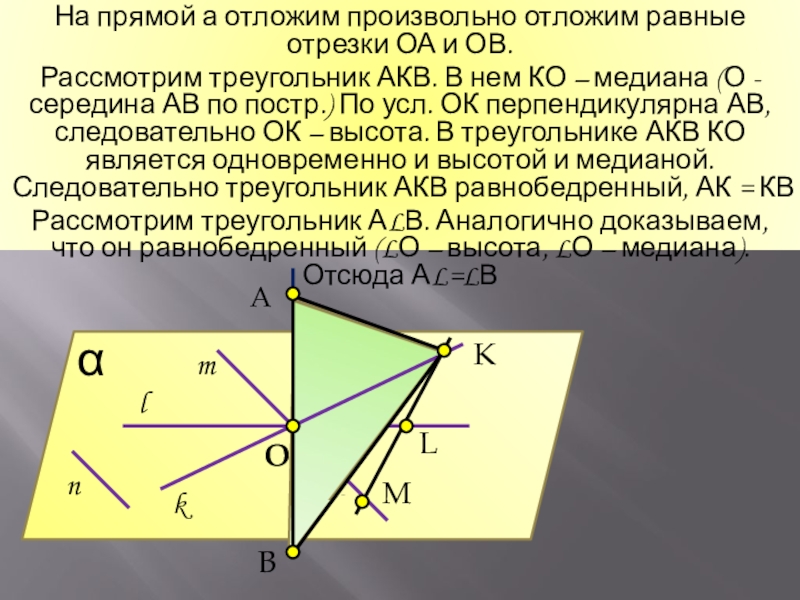
На прямой а отложим произвольно отложим равные отрезки ОА и ОВ.
Рассмотрим треугольник АКВ. В нем КО – медиана (О - середина АВ по постр.) По усл. ОК перпендикулярна АВ, следовательно ОК – высота. В треугольнике АКВ КО является одновременно и высотой и медианой. Следовательно треугольник АКВ равнобедренный, АК = КВ
Рассмотрим треугольник АLВ. Аналогично доказываем, что он равнобедренный (LО – высота, LО – медиана). Отсюда АL=LВ
а
Слайд 4A
α
K
M
L
B
O
n
l
k
m
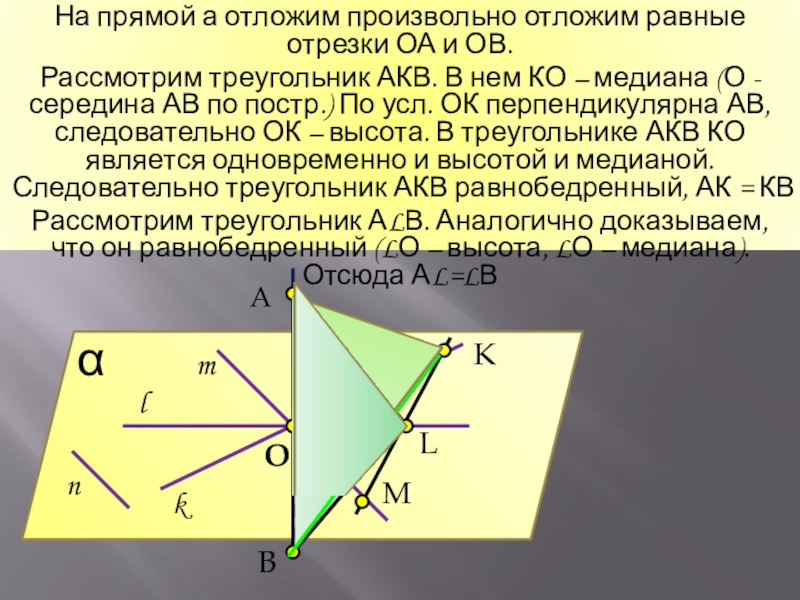
На прямой а отложим произвольно отложим равные отрезки ОА и ОВ.
Рассмотрим треугольник АКВ. В нем КО – медиана (О - середина АВ по постр.) По усл. ОК перпендикулярна АВ, следовательно ОК – высота. В треугольнике АКВ КО является одновременно и высотой и медианой. Следовательно треугольник АКВ равнобедренный, АК = КВ
Рассмотрим треугольник АLВ. Аналогично доказываем, что он равнобедренный (LО – высота, LО – медиана). Отсюда АL=LВ
а
Слайд 5A
α
K
M
L
B
O
n
l
k
m
Треугольник АКL равен треугольнику ВКL по трем сторонам (АК=КВ, АL=ВL, КL
– общая сторона). Отсюда угол АКL=углу ВКL
а
Слайд 6A
α
K
M
L
B
O
n
l
k
m
а
Треугольник АКМ равен треугольнику ВКМ по двум сторонам и углу между
ними (АК=КВ, КМ – общая сторона, угол АКМ=углу ВКМ)
Слайд 7A
α
K
M
L
B
O
n
l
k
m
а
Т. К. треугольник АКМ равен треугольнику ВКМ , то АМ=МВ. Отсюда
треугольник АМВ равнобедренный и МО в нем - медиана и высота.
В равнобедренном треугольнике высота МО является также и высотой. МО┴АВ, МО ┴а
В равнобедренном треугольнике высота МО является также и высотой. МО┴АВ, МО ┴а
Слайд 8A
α
K
M
L
B
O
n
l
k
m
а
Исходно прямая а перпендикулярна пересекающимся прямым k и l, лежащим в
плоскости α. Мы взяли произвольную прямую п и параллельную ей прямую т. Доказав, что а перпендикулярна т, мы доказали, что а перпендикулярна п – а прямая п произвольна. Т.к. а перпендикулярна любой прямой лежащей в плоскости α, то, по определению, а перпендикулярна этой плоскости.
Вывод: а┴α если а┴k и a ┴ l (k и l принадлежат плоскости α и пересекаются)
Вывод: а┴α если а┴k и a ┴ l (k и l принадлежат плоскости α и пересекаются)