- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Признак параллельности плоскостей
Содержание
- 1. Презентация по геометрии на тему Признак параллельности плоскостей
- 2. Выучить! n.12.2Задачи все разобрать и решить в тетрадь!
- 3. Вопросы и ответы:Признак параллельности прямой и плоскости?Лемма о параллельности прямых?
- 4. Параллельность прямой и плоскостиДано: точка К лежит вне плоскости параллелограмма ABCDУказать: пары параллельных прямых и плоскостейАВСDK
- 5. Параллельность прямой и плоскостиДано: точка К лежит вне плоскости трапеции ABCDДоказать: CD || (AKB)KВАСD
- 6. Параллельность прямой и плоскостиДано: плоскости
- 7. Параллельность прямой и плоскостиДано: плоскости
- 8. 07. 02. 19Классная работаПризнак параллельности плоскостей
- 9. Параллельность прямых и параллельность плоскостей связывает следующий
- 10. Доказательство. а ‖ β и b
- 11. Задачи к п. 11.212.9. Два параллелограмма ABCD
- 12. Дано: ABCD и ABC1D1 параллелограмма Доказать: (ВСС1)
- 13. Слайд 13
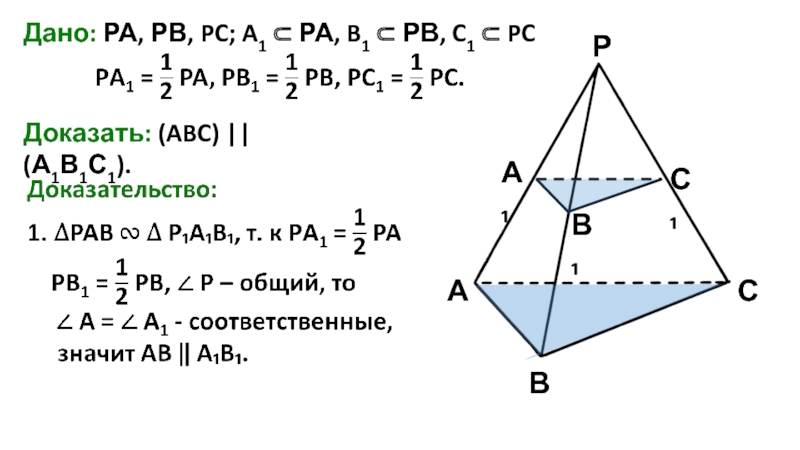
- 14. РАВСА₁В₁С₁Дано: РА, РВ, PC; A1 ⊂ РА,
- 15. РАВСА₁В₁С₁3. AВ ∩ ВС = В
- 16. 12.11. Дан параллелепипед ABCDA1B1C1D1.
- 17. Дано: ABCDA1B1C1D1 параллелепипедДоказать:а) (A1BD) ‖ (B1D1C) б)
- 18. 12.12. Две стороны треугольника параллельны плоскости α.
- 19. Домашнее задание:n. 12. 2;№№ 12.11; 12.12
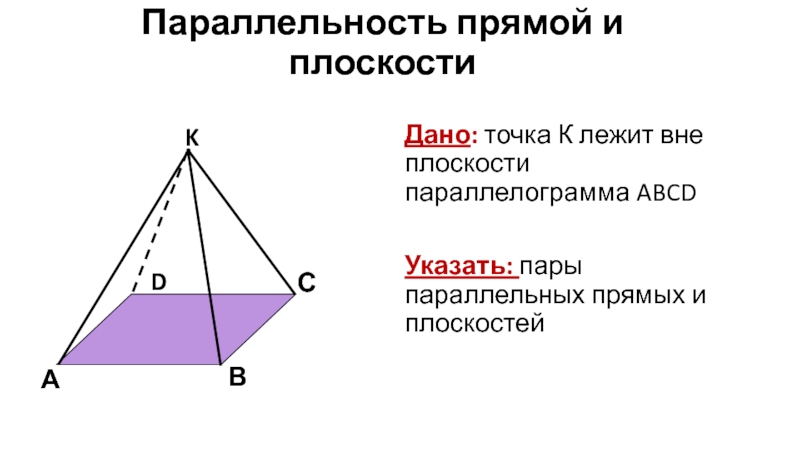
Слайд 4Параллельность прямой и плоскости
Дано: точка К лежит вне плоскости параллелограмма ABCD
Указать:
А
В
С
D
K
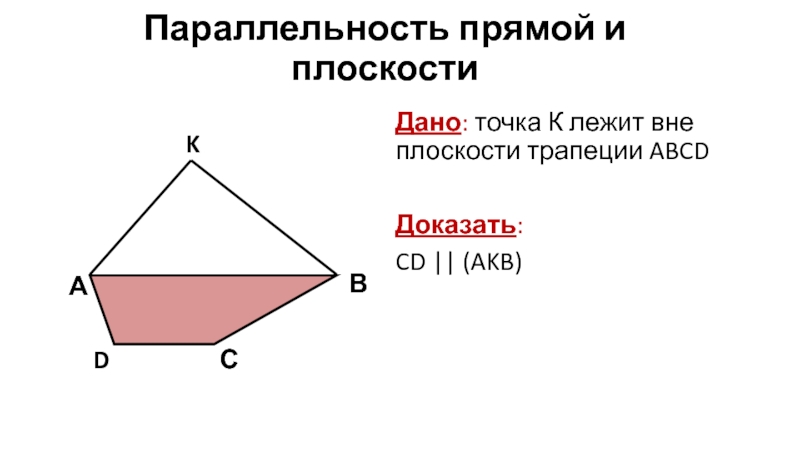
Слайд 5Параллельность прямой и плоскости
Дано: точка К лежит вне плоскости трапеции ABCD
Доказать:
CD || (AKB)
K
В
А
С
D
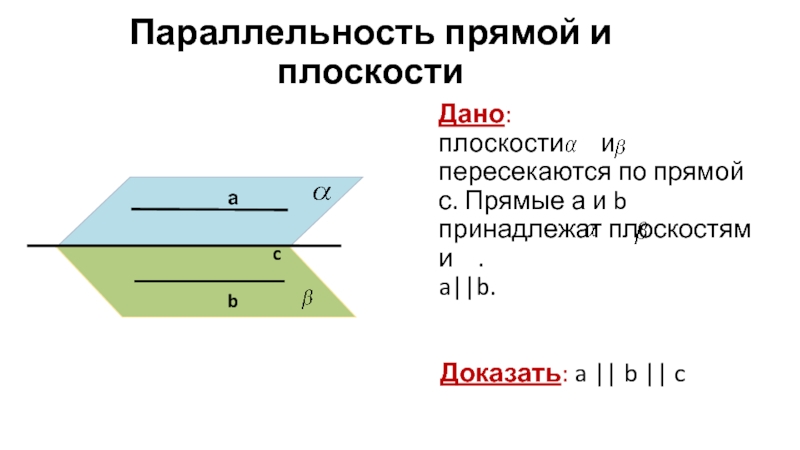
Слайд 6Параллельность прямой и плоскости
Дано:
плоскости и пересекаются
a||b.
Доказать: a || b || c
а
b
c
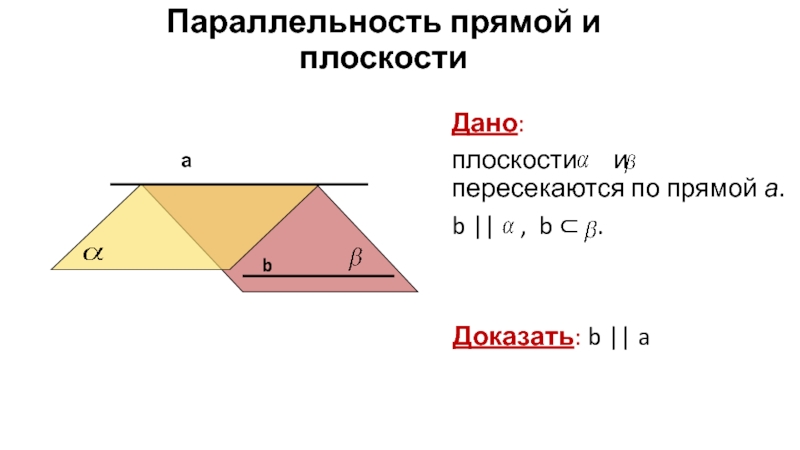
Слайд 7Параллельность прямой и плоскости
Дано:
плоскости и пересекаются
b || , b ⊂ .
Доказать: b || a
а
b
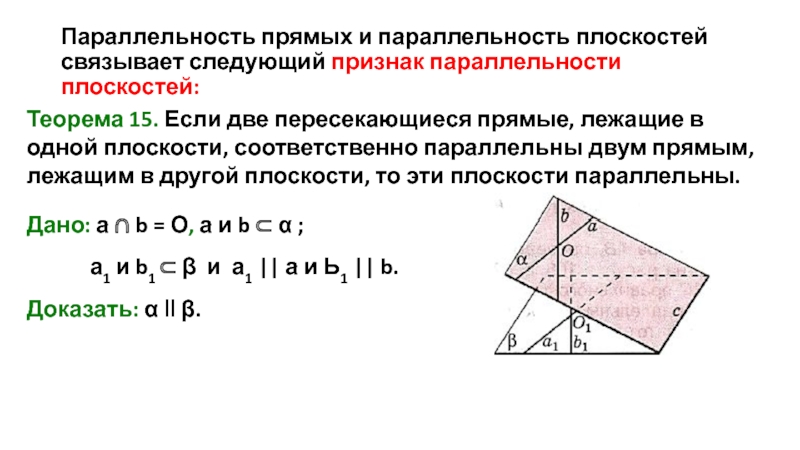
Слайд 9Параллельность прямых и параллельность плоскостей связывает следующий признак параллельности плоскостей:
Теорема 15.
Дано: а ∩ b = О, а и b ⊂ α ;
а1 и b1 ⊂ β и а1 || а и Ь1 || b.
Доказать: α ‖ β.
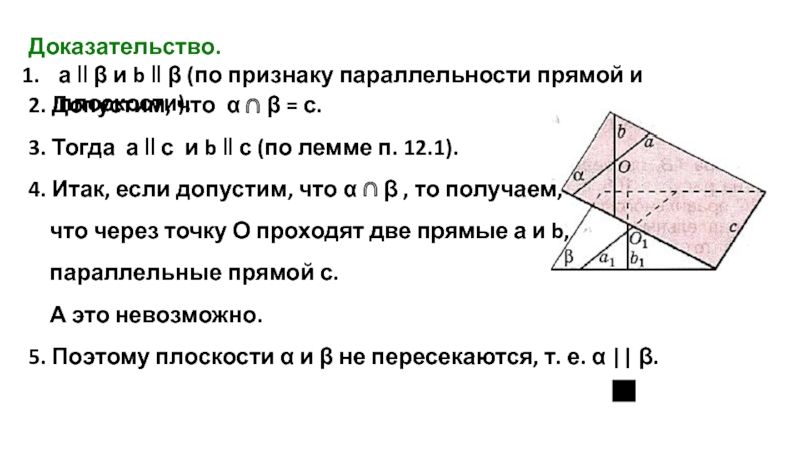
Слайд 10Доказательство.
а ‖ β и b ‖ β (по признаку
2. Допустим, что α ∩ β = с.
3. Тогда а ‖ с и b ‖ с (по лемме п. 12.1).
4. Итак, если допустим, что α ∩ β , то получаем,
что через точку О проходят две прямые а и b,
параллельные прямой с.
А это невозможно.
5. Поэтому плоскости α и β не пересекаются, т. е. α || β.
Слайд 11Задачи к п. 11.2
12.9. Два параллелограмма ABCD и ABC1D1 не лежат в
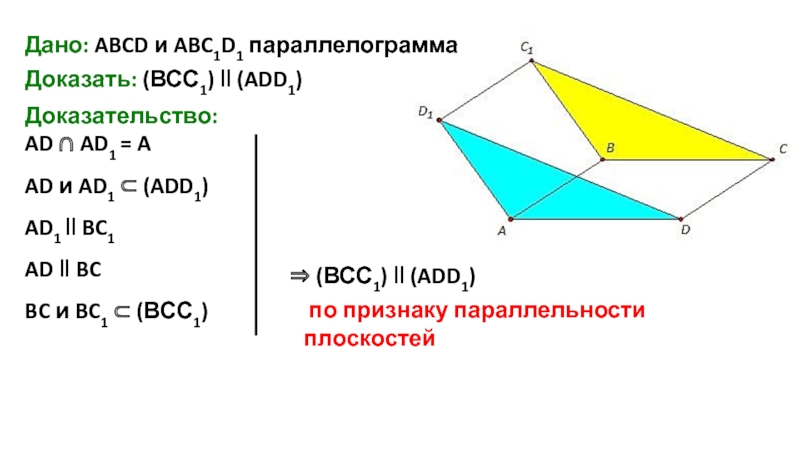
Слайд 12Дано: ABCD и ABC1D1 параллелограмма
Доказать: (ВСС1) ‖ (ADD1)
Доказательство:
AD ∩
AD и AD1 ⊂ (ADD1)
AD1 ‖ BC1
AD ‖ BC
BC и BC1 ⊂ (ВСС1)
⇒ (ВСС1) ‖ (ADD1)
по признаку параллельности плоскостей
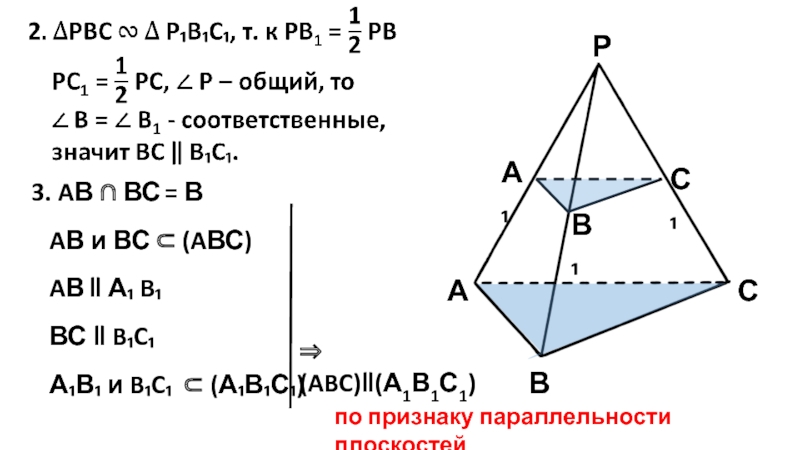
Слайд 15Р
А
В
С
А₁
В₁
С₁
3. AВ ∩ ВС = В
AВ и ВС ⊂
AВ ‖ А₁ B₁
ВС ‖ B₁C₁
А₁В₁ и B₁C₁ ⊂ (А₁В₁С₁)
⇒ (ABC)‖(А1В1С1)
по признаку параллельности плоскостей
Слайд 1612.11. Дан параллелепипед ABCDA1B1C1D1.
б) Укажите аналогичные пары параллельных сечений
параллелепипеда.
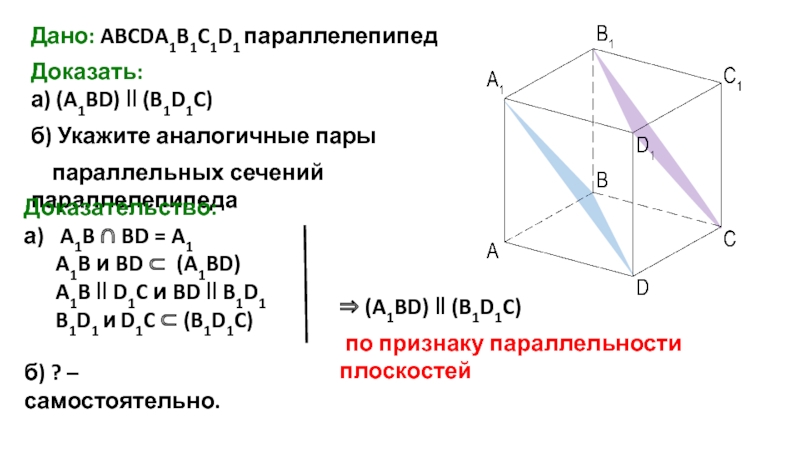
Слайд 17Дано: ABCDA1B1C1D1 параллелепипед
Доказать:
а) (A1BD) ‖ (B1D1C)
б) Укажите аналогичные пары
Доказательство:
а) A1B ∩ BD = A1
A1B и BD ⊂ (A1BD)
A1B ‖ D1C и BD ‖ B1D1
B1D1 и D1C ⊂ (B1D1C)
⇒ (A1BD) ‖ (B1D1C)
б) ? – самостоятельно.
по признаку параллельности плоскостей
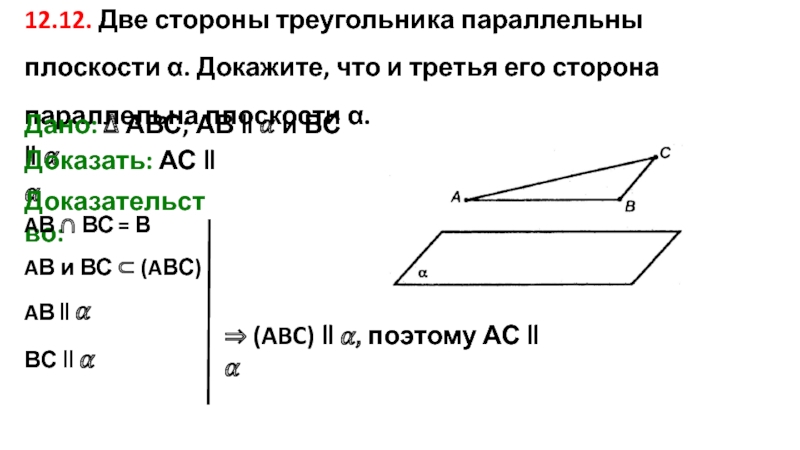
Слайд 1812.12. Две стороны треугольника параллельны плоскости α. Докажите, что и третья
Дано: ∆ АВС; АВ ‖ ? и ВС ‖ ?
Доказать: АС ‖ ?
Доказательство:
AВ ∩ ВС = В
AВ и ВС ⊂ (AВС)
AВ ‖ ?
ВС ‖ ?
⇒ (ABC) ‖ ?, поэтому АС ‖ ?