- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Преобразование подобия и его простейшие свойства
Содержание
- 1. Презентация по геометрии на тему Преобразование подобия и его простейшие свойства
- 2. Выучить! n.10.1Задачи все разобрать и решить в тетрадь!
- 3. 07. 02. 19Классная работаПреобразование подобия и его простейшие свойства
- 4. Второй важный класс преобразований, который мы изучим, - это преобразования подобия.
- 5. Реальное преобразование подобия происходит каждый раз, когда
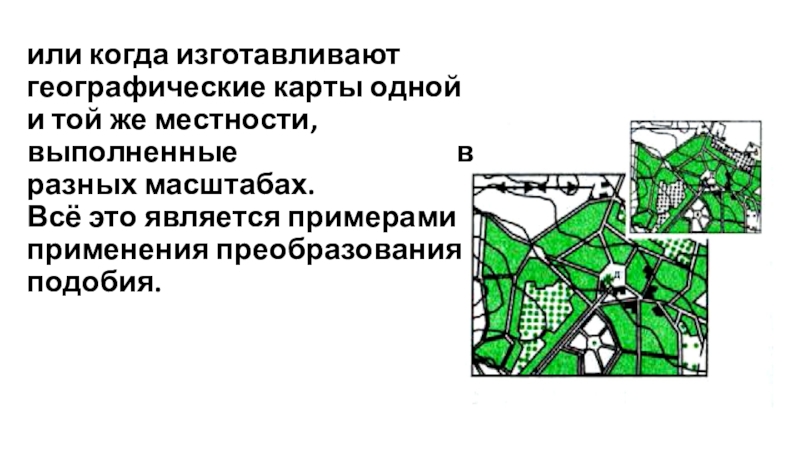
- 6. или когда изготавливают географические карты одной и
- 7. В приведённых примерах происходит преобразование одной фигуру
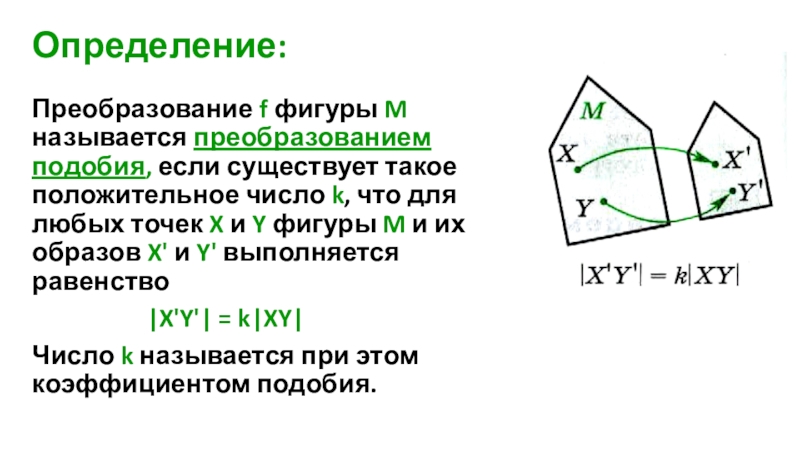
- 8. Определение:Преобразование f фигуры M называется преобразованием подобия,
- 9. Из приведенного определения следует, что,
- 10. 1. Действительно, если точки X и
- 11. Слайд 11
- 12. Наконец, отметим, что композиция подобий с коэффициентами
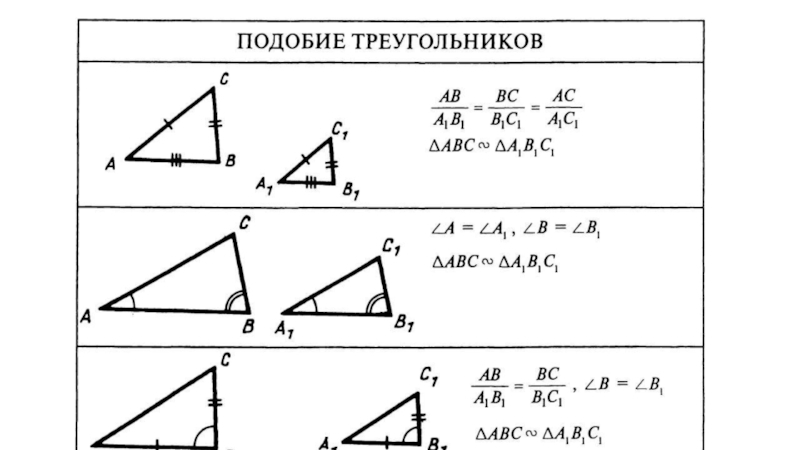
- 13. Говорят, что фигура P подобна фигуре M
- 14. Вопросы для самоконтроля В чем заключается подобное
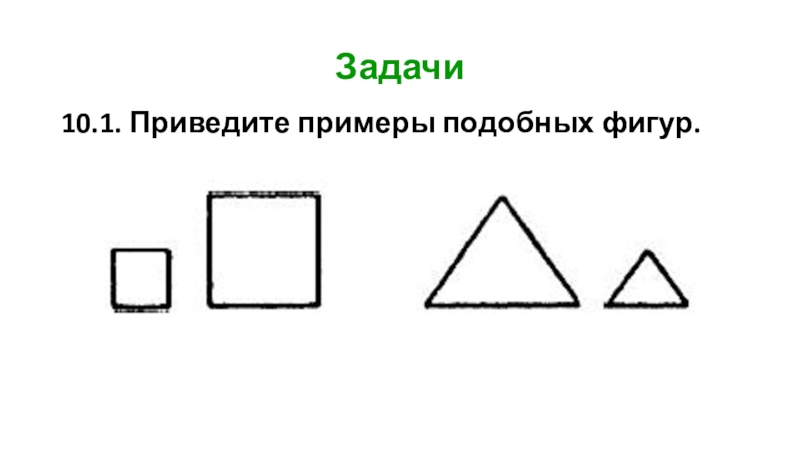
- 15. Задачи 10.1. Приведите примеры подобных фигур.
- 16. 10.2 Придумайте признаки подобия а) прямоугольников; б)
- 17. Слайд 17
- 18. 10.4. Каков коэффициент подобия Гулливера и лилипута?
- 19. Доказываем. 10.5. Докажите, что любые две окружности
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
Слайд 5Реальное преобразование подобия происходит каждый раз, когда печатают фотографию с негатива
или когда кадры киноплёнки проектируются на экран, или когда создают модели реальных предметов (самолётов, кораблей, автомобилей),
Слайд 6или когда изготавливают географические карты одной и той же местности, выполненные
Слайд 7В приведённых примерах происходит преобразование одной фигуру в другую (подобную первой),
Слайд 8Определение:
Преобразование f фигуры M называется преобразованием подобия, если существует такое положительное
|X'Y'| = k|XY|
Число k называется при этом коэффициентом подобия.
Слайд 9Из приведенного определения следует, что,
Слайд 10 1. Действительно, если точки X и Y различны, то |XY|>
Слайд 12Наконец, отметим, что композиция подобий с коэффициентами k₁ и k₂ есть
Действительно, пусть подобие f с коэффициентом k₁ переводит фигуру M в фигуру P = f(M), а затем подобие g с коэффициентом k₂ переводит фигуру P в фигуру g(P)
Тогда их композиция g • f переводит фигуру M в фигуру g(P). Если X и Y - произвольные точки фигуры M, то
|X′Y′ | = k₁|XY|, где X′ = f(X) и Y′ = f(Y). Далее, если X′′ = g(X′) и Y′′ = g(Y′), то
|X′′Y′′ |= k₂|X′Y′|.
Поэтому
|X′′Y′′| = k₁k₂|XY| .
Итак, g • f является подобием с коэффициентом k₁k₂.
Слайд 13Говорят, что фигура P подобна фигуре M
Слайд 14Вопросы для самоконтроля
В чем заключается подобное преобразование фигуры?
Какие фигуры
Что такое коэффициент подобия?
Почему преобразование подобия обратимо? Чем является преобразование, обратное к преобразованию подобия с коэффициентом k?
Чем является композиция двух преобразований подобия?
Может ли подобие быть движением?
Слайд 1610.2 Придумайте признаки подобия а) прямоугольников; б) ромбов;
Решение:
а) Два прямоугольника подобны, если их стороны пропорциональны;
б) Два ромбов(отличные от квадрата ) подобны, если их острые
углы равны;
в) Два параллелограмма подобны, если их стороны пропорциональны
и соответственные углы равны;
г) Два прямоугольных параллелепипедов подобны если их
измерения пропорциональны.
Слайд 1810.4. Каков коэффициент подобия Гулливера и лилипута? Гулливера и великана? Дюймовочки
Слайд 19Доказываем.
10.5. Докажите, что любые две окружности подобны.
10.6. Докажите, что
Применяем геометрию.
10.7. Как по плану местности (или по карте) определить расстояние между двумя объектами?