г. Нефтеюганск Некдаров Х.Л.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Правильные многоугольники (9 класс)
Содержание
- 1. Презентация по геометрии на тему Правильные многоугольники (9 класс)
- 2. Данная тема является частью темы «Правильные многоугольники»,
- 3. Цель урока: 1) Закрепление изученного на
- 4. Учащиеся должны: знать: -определение правильного многоугольника;
- 5. Оборудование: компьютер,
- 6. I. Повторение.1. Правильный многоугольник - ?2. Формула
- 7. 1.Учащиеся по очереди комментируют решение задач, при
- 8. 1) Найти величину каждого угла для пятиугольника
- 9. 2) Докажите, что треугольник, две высоты АТ
- 10. 3) Окружность радиусом 5 см касается сторон
- 11. 4) Две окружности пересекаются в точках А
- 12. 5) Докажите, что радиус окружности, вписанной в
- 13. 6) Четырёхугольник ABCD вписан в окружность. Докажите,
- 14. 2. Изучение новой темыПрочитайте по учебнику формулировку
- 15. 3. Решить задачи:Докажите, что в правильном пятиугольнике
- 16. 4. Итоги урока5. Домашнее задание: п.
- 17. Спасибо за внимание
Данная тема является частью темы «Правильные многоугольники», которая в свою очередь находит широкое применение при изучении тем «Длина окружности» и «Площадь круга»
Слайд 2Данная тема является частью темы «Правильные многоугольники», которая в свою очередь
находит широкое применение при изучении тем «Длина окружности» и «Площадь круга»
Слайд 3Цель урока: 1) Закрепление изученного на первом уроке материала; 2) Изучение
теоремы об окружности вписанной в правильный многоугольник и следствий из них.
Слайд 4Учащиеся должны: знать: -определение правильного многоугольника; -формулу для вычисления угла
правильного n – угольника;
-формулировку и доказательство теоремы об окружностях, описанной около правильного многоугольника и вписанной в него;
-следствия из второй теоремы;
уметь – применять эти знания при решении задач.
Слайд 6I. Повторение.
1. Правильный многоугольник - ?
2. Формула для вычисления угла правильного
многоугольника - ?
3. Решение задач.
(Все учащиеся получают карточки задач с печатной основой)
3. Решение задач.
(Все учащиеся получают карточки задач с печатной основой)
Слайд 71.Учащиеся по очереди комментируют решение задач, при этом решение посредством анимации
появляется на экране. Все учащиеся делают записи в своих карточках. При этом внимание учителя на учащихся, а не на доске, экономия времени, дизайн, образец краткой записи решения задач для учащихся.
2. Данный электронный вариант решения задач может использоваться учащимися как тренажёр для решения задач такого типа.
Слайд 81) Найти величину каждого угла для пятиугольника ABCDE.
В данном пятиугольнике все
стороны равны и все углы равны, значит этот пятиугольник правильный.
Тогда:
Решение.
Слайд 92) Докажите, что треугольник, две высоты АТ и СМ которого равны,
является равнобедренным
Решение.
Рассмотрим треугольники AMC и CTА:
1) Треугольники прямоугольные, т.к. AT и CM высоты треугольника ABC - по условию;
2)AC – общая гипотенуза;
3) AT=CM-по условию;
4) Треугольники AMC и CTA равны по гипотенузе (АС) и катету (АТ и СМ).
Значит А и В равны
5) Треугольник ABC – равнобедренный (по признаку равнобедренного треугольника), что и требовалось доказать.
Слайд 103) Окружность радиусом 5 см касается сторон угла A в точках
B и C. Найдите длины отрезков AB и AC, если центр окружности удалён от вершины угла на 13см.
Решение
1) AB=AС – отрезки касательных проведённых из одной точки A
2) Построим радиусы OB и OC.
3)
(радиусы проведённые в точки касания прямых AB и AC и окружности).
4) - прямоугольные
- по трём сторонам
5)
Ответ: AB=AC=12 см.
Слайд 114) Две окружности пересекаются в точках А и В. Докажите, что
прямая, проходящая через их центры, перпендикулярна к отрезку АВ.
Решение
1) Построим радиусы OA, OB, MB, МА.
2) (3 признак: OM – общая сторона; OA=OB – радиусы; MA=MB – радиусы).
3) Из (2) следует, что AMO = BMO, значит MO – биссектриса угла AMB
4) т.к. - равнобедренный, то биссектриса, проведённая из вершины M, является высотой .
Значит , что и требовалось доказать.
Слайд 125) Докажите, что радиус окружности, вписанной в равносторонний треугольник, вдвое меньше
радиуса описанной около него окружности.
Решение
1) Построим AA1 и BB1 – биссектрисы углов А и В.
2) В равностороннем треугольнике биссектриса является и высотой и медианой.
3) Радиус описанной окружности R=ОА=ОВ=ОС
4) Радиус вписанной окружности r= OA1=OB1
- (Медианы в точке пересечения
делятся в отношении 2:1,
считая от вершины).
6)Тогда , что и требовалось доказать.
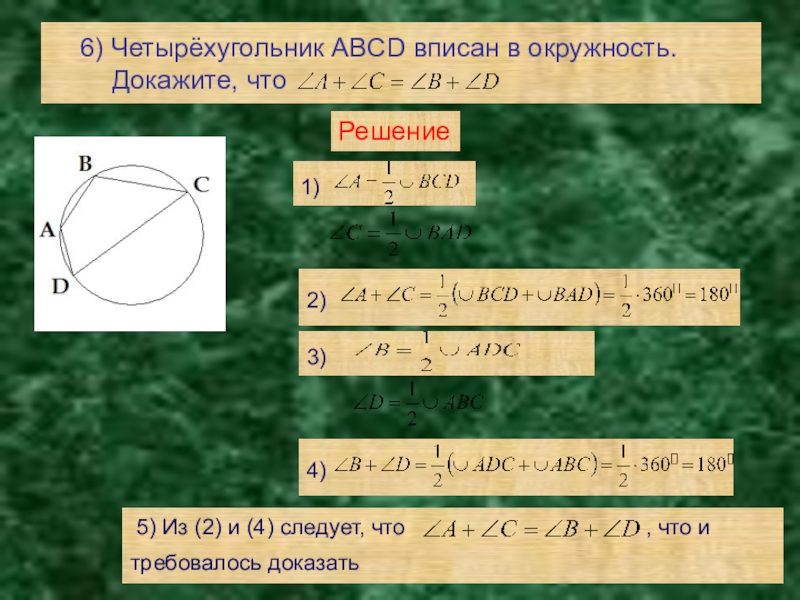
Слайд 136) Четырёхугольник ABCD вписан в окружность. Докажите, что
2)
1)
3)
Решение
4)
5) Из (2) и (4) следует, что , что и требовалось доказать
Слайд 142. Изучение новой темы
Прочитайте по учебнику формулировку и доказательство теоремы об
окружности, вписанной в правильный многоугольник, и следствия из этой теоремы
Слайд 153. Решить задачи:
Докажите, что в правильном пятиугольнике все диагонали равны.
2) На
каждой из сторон квадрата отмечены две точки, делящие стороны в отношении . Докажите, что эти точки служат вершинами правильного восьмиугольника.
3) №1082
3) №1082
Слайд 164. Итоги урока
5. Домашнее задание:
п. 105 – 107, вопросы 1
- 4 (стр. 290).
№ 1080, 1081 (д), 1084(д,е).
№ 1080, 1081 (д), 1084(д,е).
