- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему: Правильная пирамида ( 10 класс)
Содержание
- 1. Презентация по геометрии на тему: Правильная пирамида ( 10 класс)
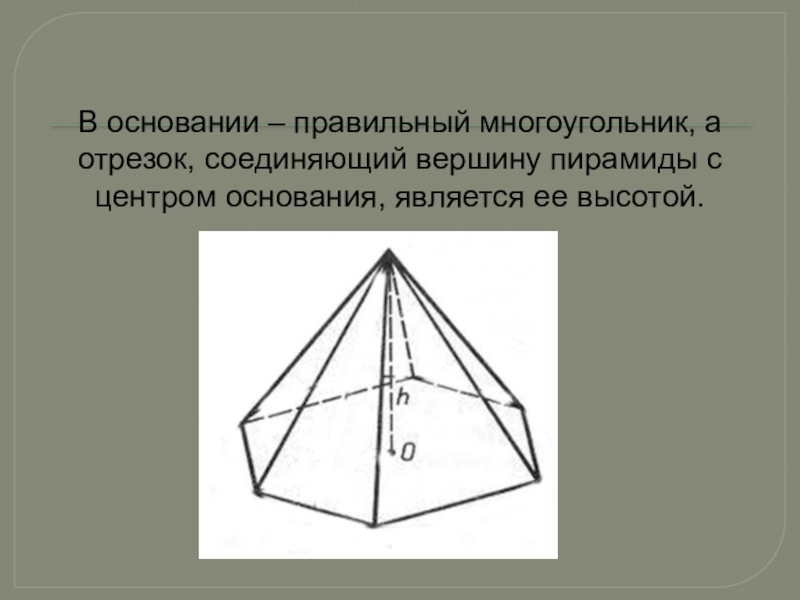
- 2. В основании – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
- 3. Доказать: 1)АnР=А1Р=А2Р…,2) АnРА1,А1РА2,…-равные равнобедренные
- 4. АпофемаАпофема-высота боковой грани правильной пирамиды, проведенная из вершиныпирамиды.PE ┴ A1A2
- 5. Слайд 5
В основании – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
Слайд 1Учитель математики Носова Татьяна Николаевна
МБОУ СОШ №5 г.Николаевск-на-Амуре Хабаровского края
2014-2015
Правильная пирамида
Слайд 2В основании – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с
центром основания, является ее высотой.
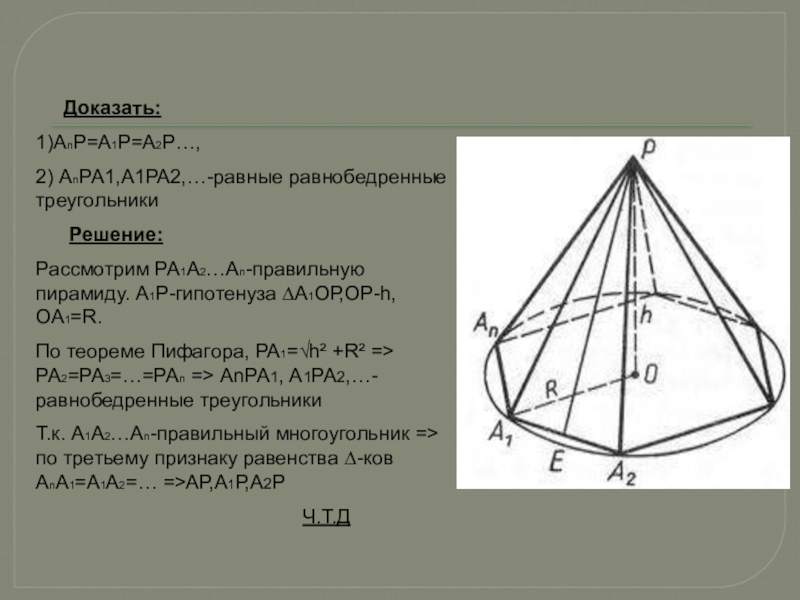
Слайд 3 Доказать:
1)АnР=А1Р=А2Р…,
2) АnРА1,А1РА2,…-равные равнобедренные треугольники
Решение:
Рассмотрим
РА1А2…Аn-правильную пирамиду. А1Р-гипотенуза ∆А1ОР,ОР-h,ОА1=R.
По теореме Пифагора, РА1=√h² +R² => РА2=РА3=…=РАn => АnРА1, А1РА2,…- равнобедренные треугольники
Т.к. А1А2…Аn-правильный многоугольник => по третьему признаку равенства ∆-ков АnА1=А1А2=… =>АР,А1Р,А2Р
Ч.Т.Д
По теореме Пифагора, РА1=√h² +R² => РА2=РА3=…=РАn => АnРА1, А1РА2,…- равнобедренные треугольники
Т.к. А1А2…Аn-правильный многоугольник => по третьему признаку равенства ∆-ков АnА1=А1А2=… =>АР,А1Р,А2Р
Ч.Т.Д
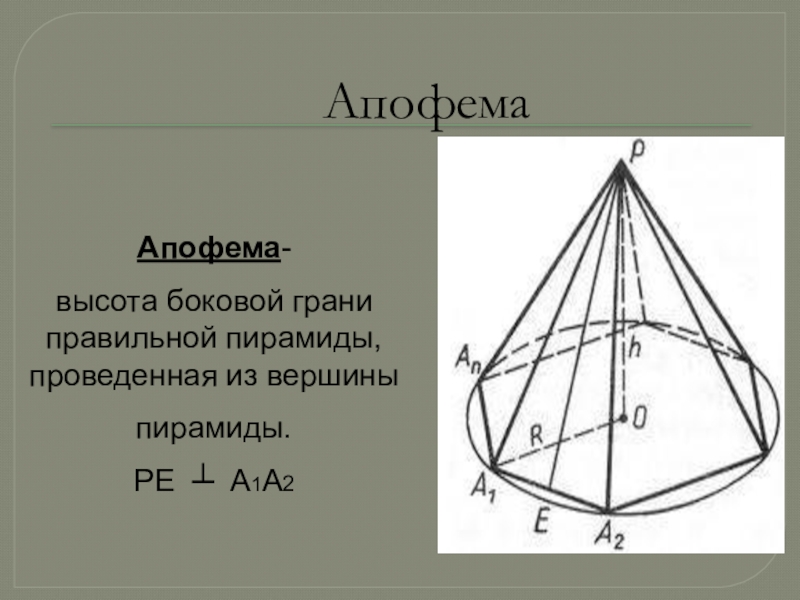
Слайд 4Апофема
Апофема-
высота боковой грани правильной пирамиды, проведенная из вершины
пирамиды.
PE ┴ A1A2
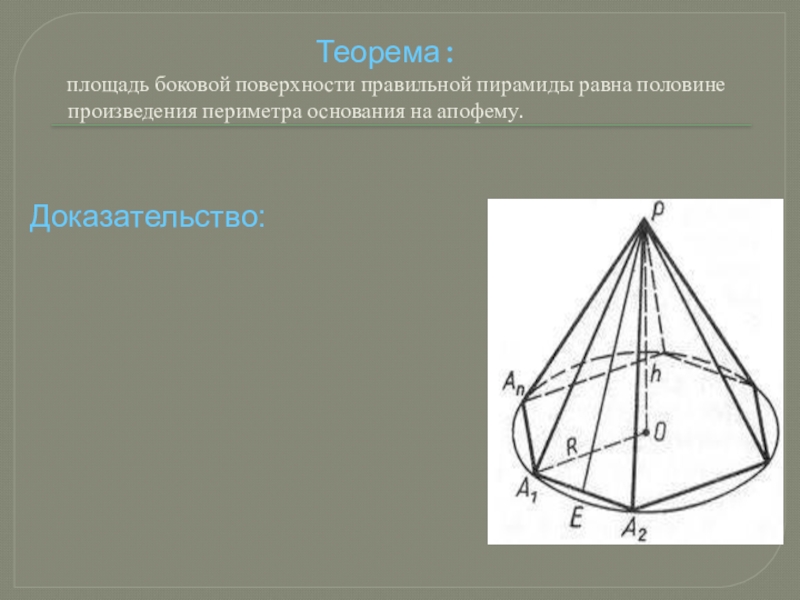
Слайд 5 Теорема:
площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Доказательство: