- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Понятие вектора (9 класс)
Содержание
- 1. Презентация по геометрии на тему Понятие вектора (9 класс)
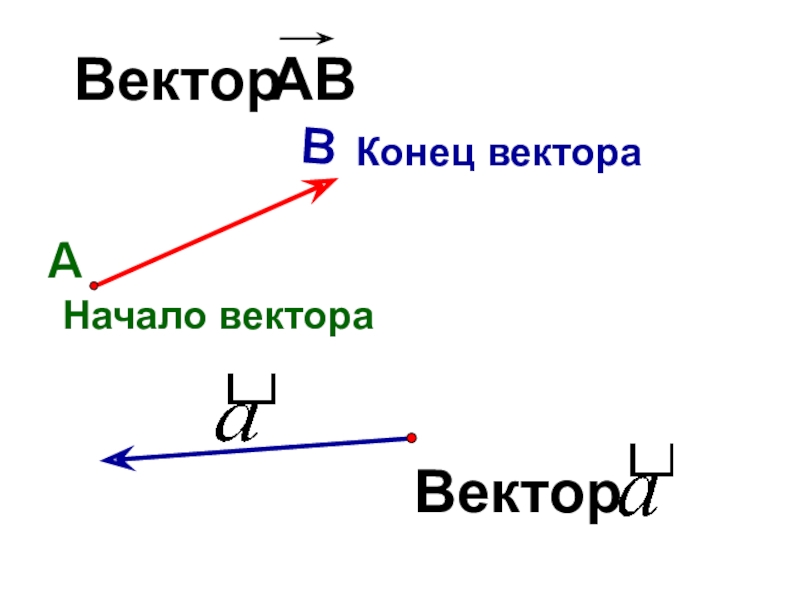
- 2. Отрезок, для которого указано,
- 3. Конец вектораНачало вектора
- 4. Любая точка плоскости также является вектором. В этом случае вектор называется нулевымM
- 5. Начало нулевого вектора совпадает с его концом, поэтому нулевой вектор не имеет какого-либо определенного направления
- 6. Любое направление можно считать направлением нулевого вектора
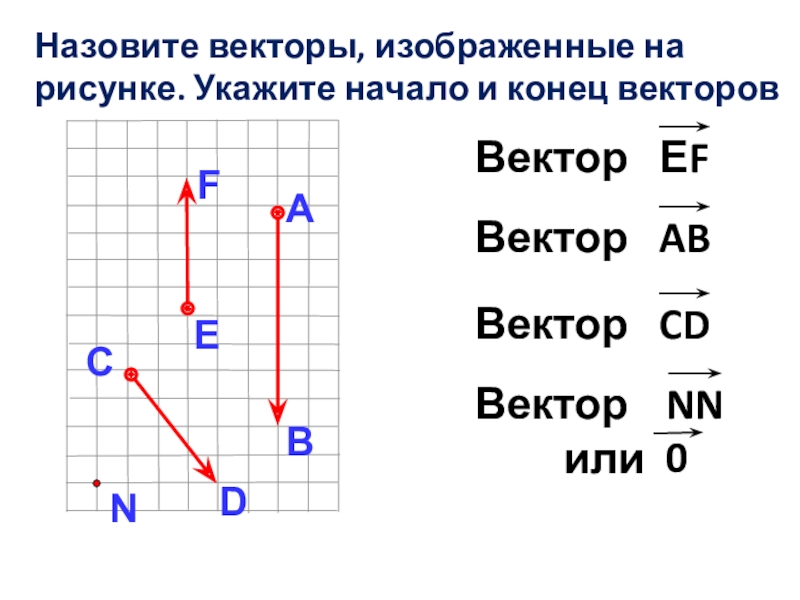
- 7. Назовите векторы, изображенные на рисунке. Укажите начало и конец векторов
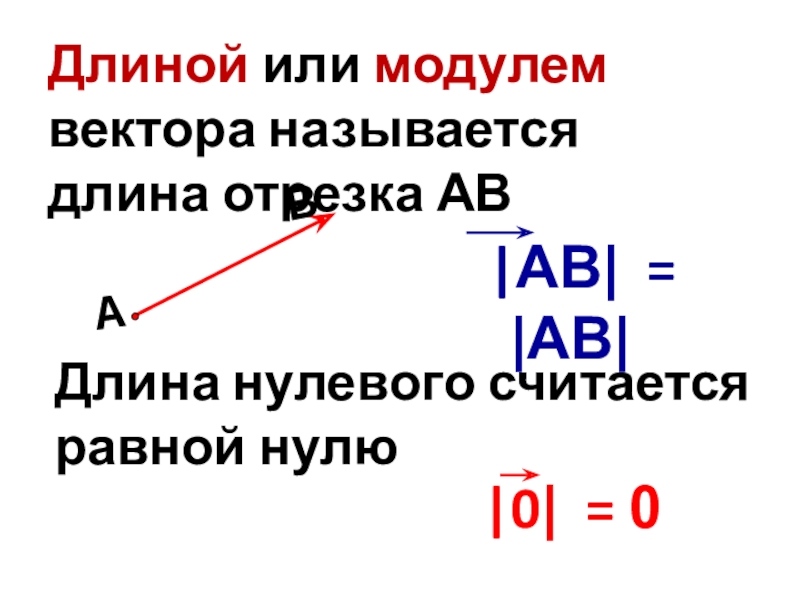
- 8. Длиной или модулем вектора называется длина отрезка АВДлина нулевого считается равной нулю
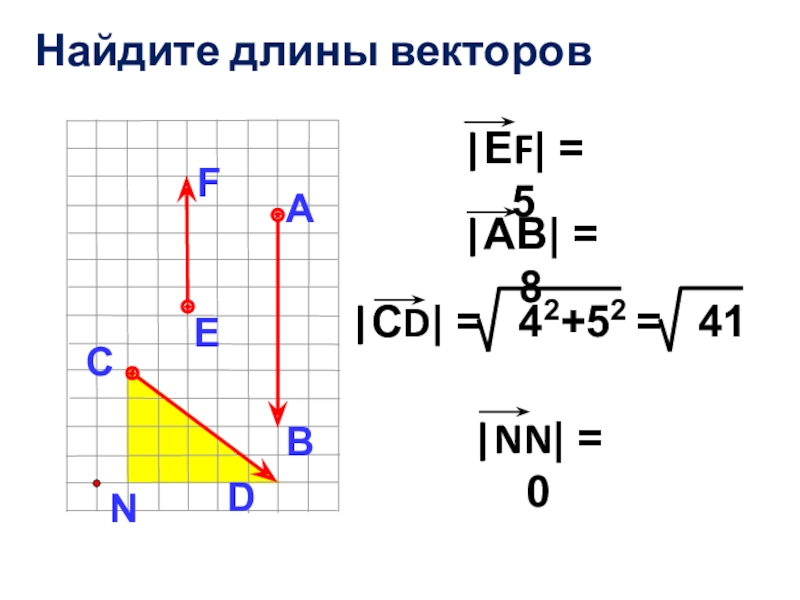
- 9. Найдите длины векторов|ЕF| = 5 |АВ| = 8 |NN| = 0
- 10. Многие физические величины, например сила, перемещение материальной
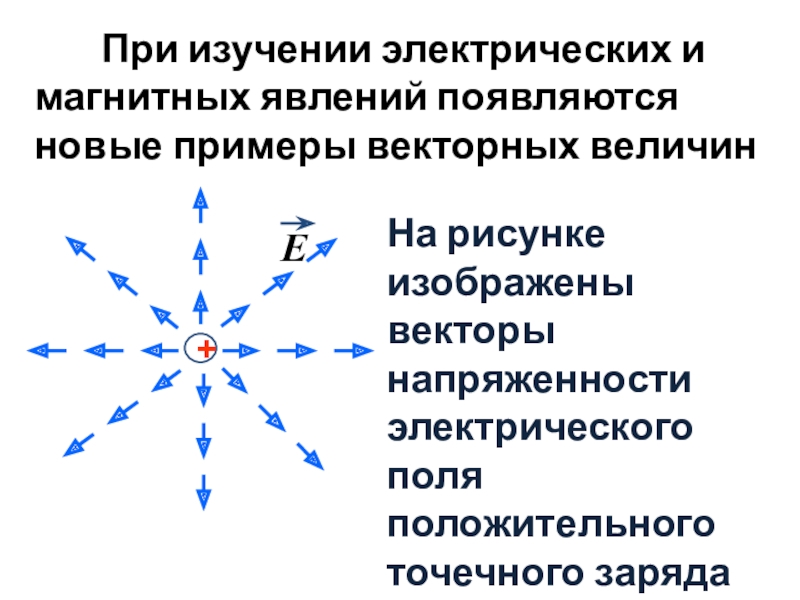
- 11. При изучении электрических и магнитных явлений появляются новые примеры векторных величин
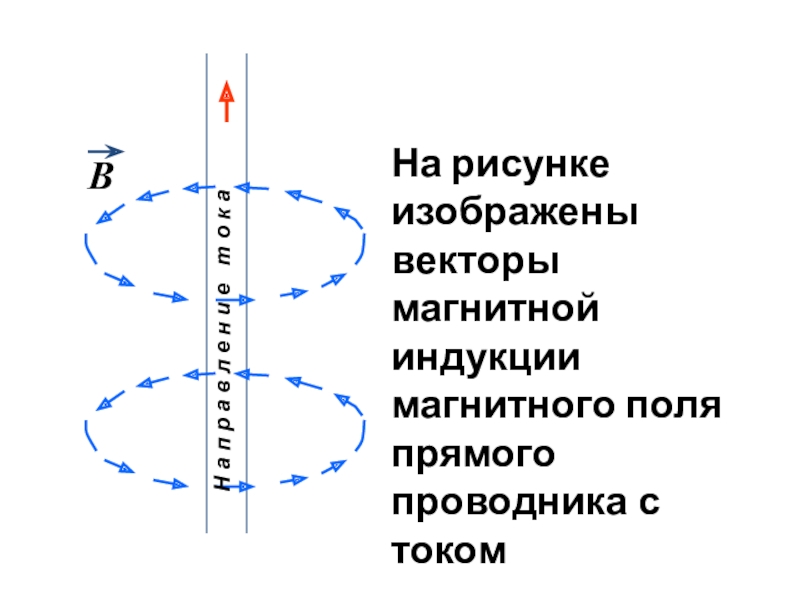
- 12. На рисунке изображены векторы магнитной индукции магнитного поля прямого проводника с током
- 13. Ненулевые векторы называются коллинеарными, если
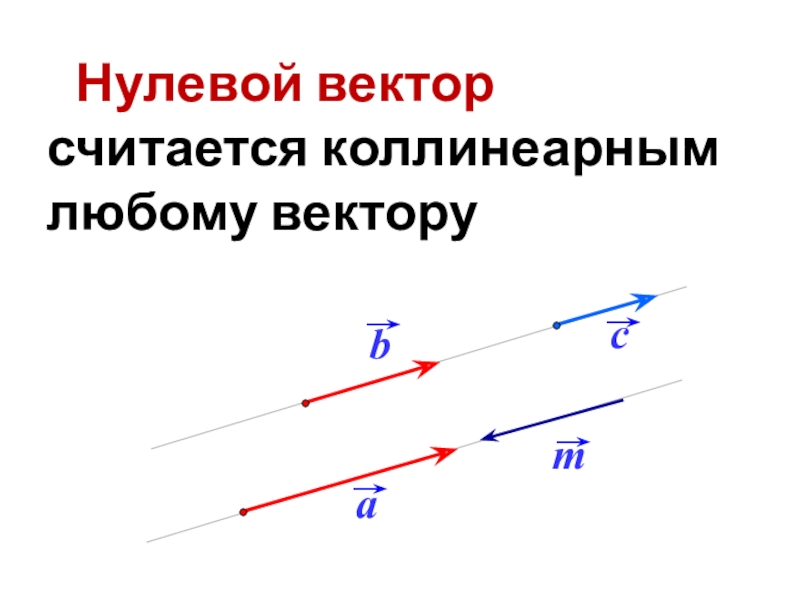
- 14. Нулевой вектор считается коллинеарным любому вектору
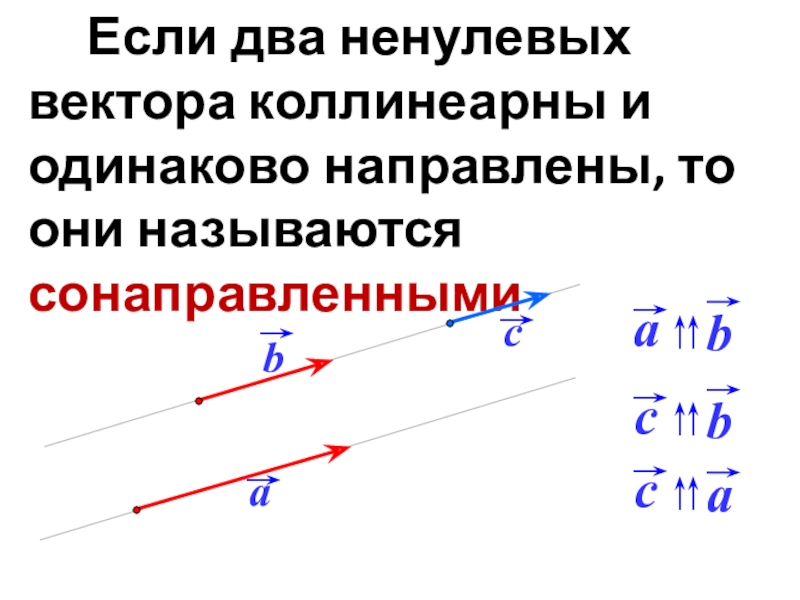
- 15. Если два ненулевых вектора коллинеарны и одинаково направлены, то они называются сонаправленными
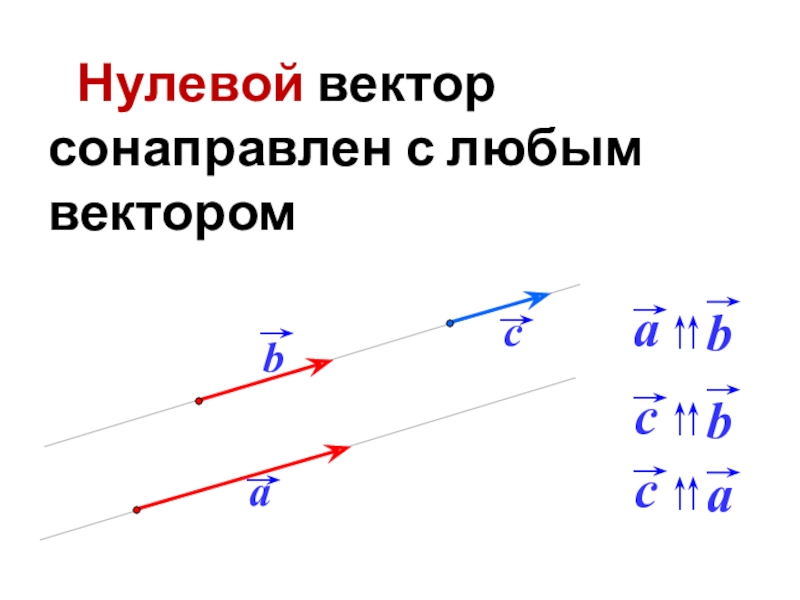
- 16. Нулевой вектор сонаправлен с любым вектором
- 17. Если два ненулевых вектора коллинеарны и направлены противоположно, то они называются противоположно направленными
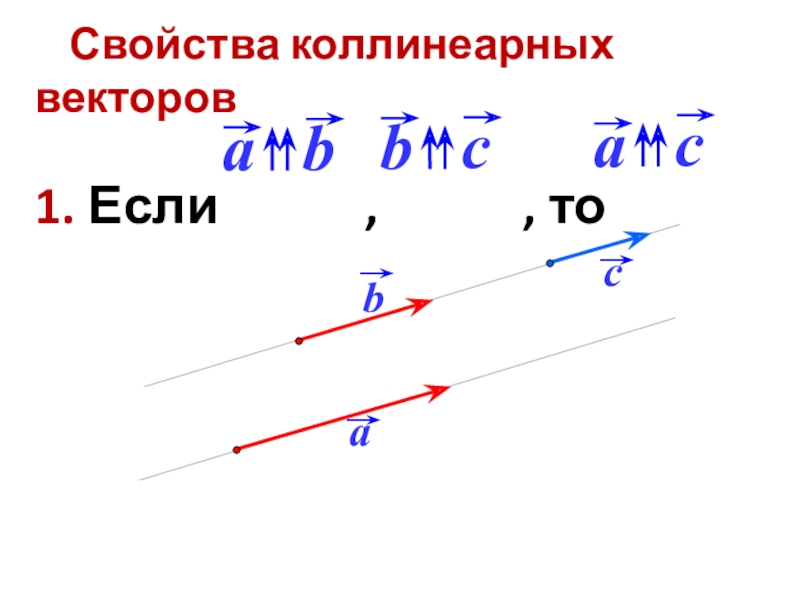
- 18. Свойства коллинеарных векторов1. Если
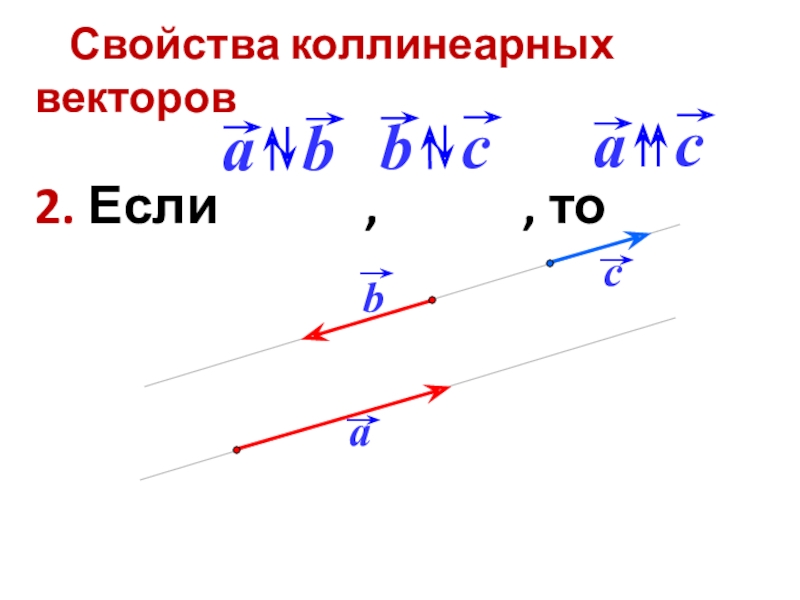
- 19. Свойства коллинеарных векторов2. Если
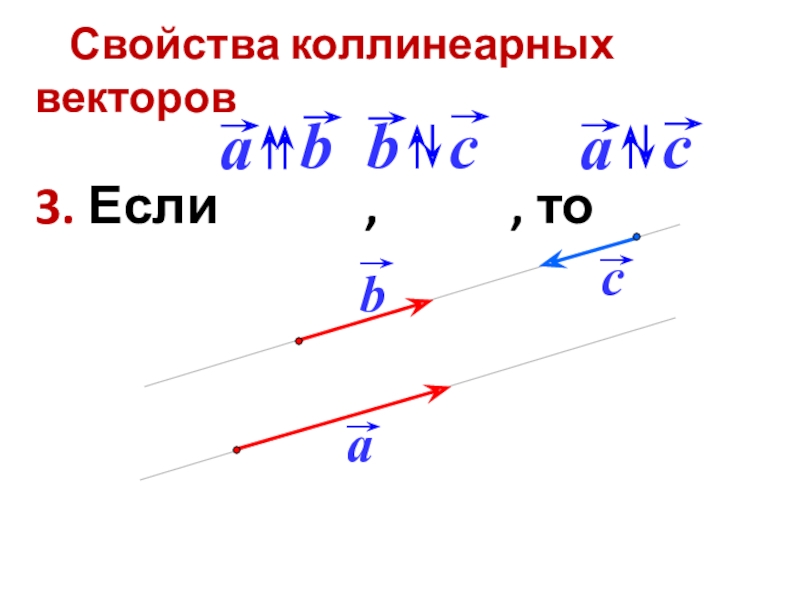
- 20. Свойства коллинеарных векторов3. Если
- 21. Векторы называются равными, если они сонаправлены и их длины равныab
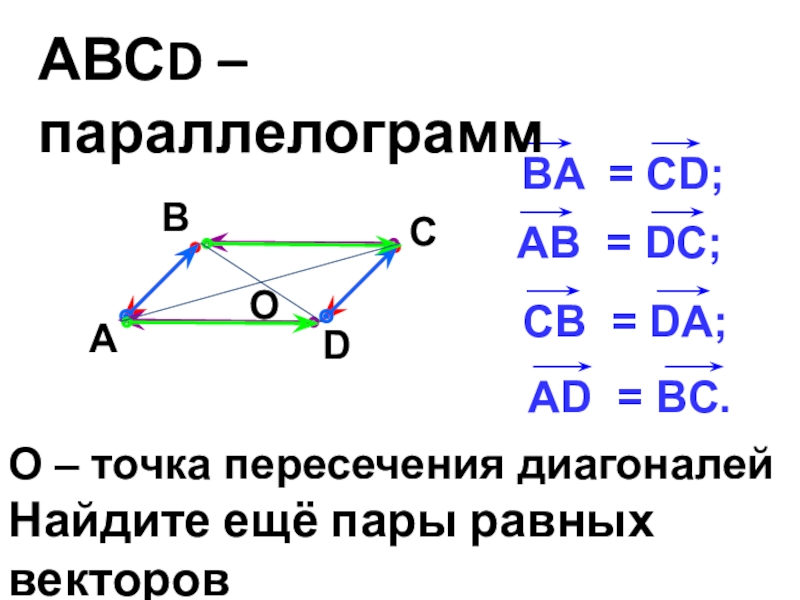
- 22. О – точка пересечения диагоналейНайдите ещё пары равных векторовАВСD – параллелограмм
- 23. САВD43M № 745. В прямоугольнике АВСD
- 24. Решение задач№ 740№ 738№ 742
- 25. Если точка M –
- 26. От любой точки М можно отложить вектор,
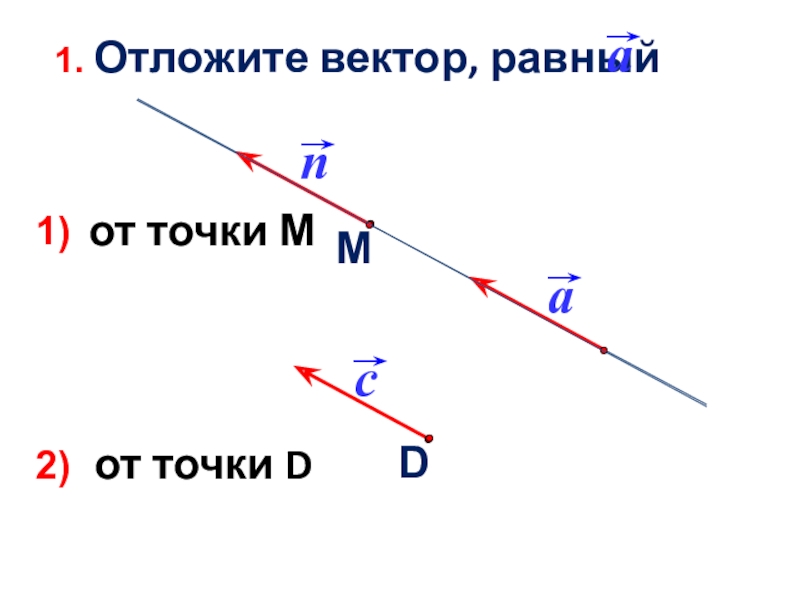
- 27. от точки М от точки D 1)2)
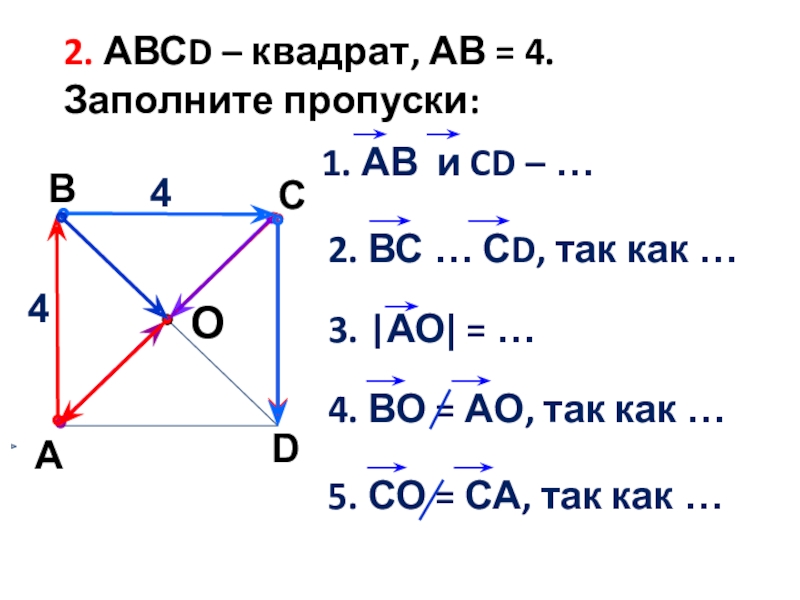
- 28. 2. АВСD – квадрат, АВ = 4. Заполните пропуски:3. |АО| = … 44
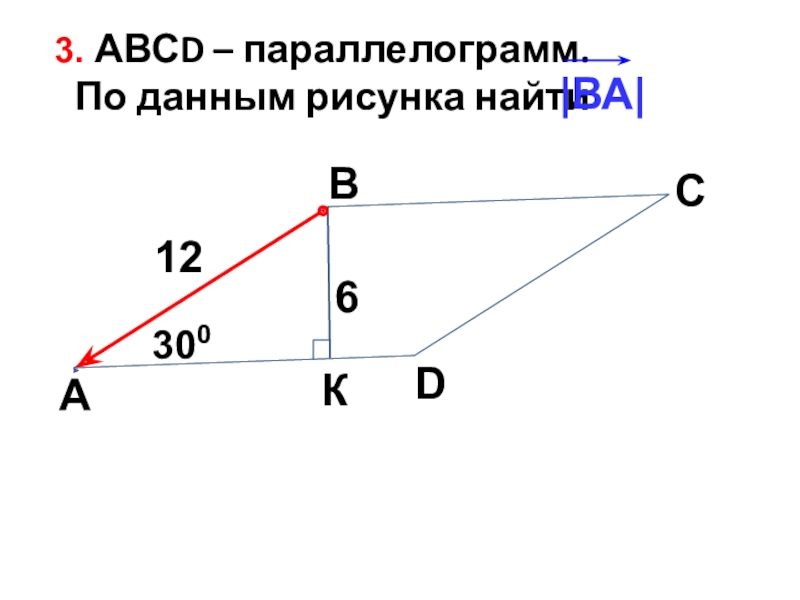
- 29. 3. АВСD – параллелограмм. По данным рисунка найти АВСD3006К12
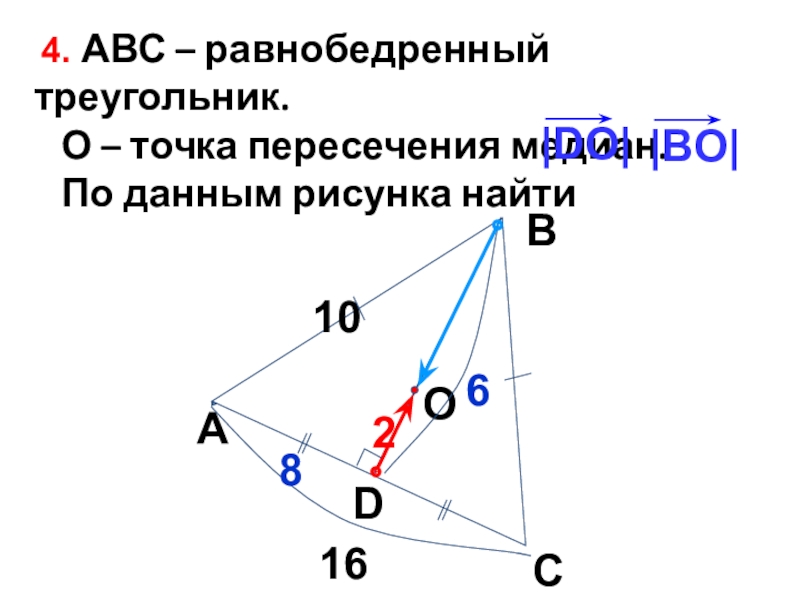
- 30. 4. АВС – равнобедренный треугольник.
- 31. Решение задач№ 743№ 750№ 751
- 32. Домашнее заданиепп. 76 – 78Определения выучить№ 741№ 746№ 747№ 748№ 749№ 752
- 33. Список литературыАтанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.
Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется направленным отрезком или вектором
Слайд 2 Отрезок, для которого указано, какой из его концов
считается началом, а какой – концом, называется направленным отрезком или вектором
Слайд 5Начало нулевого вектора совпадает с его концом, поэтому нулевой вектор не
имеет какого-либо определенного направления
Слайд 10
Многие физические величины, например сила, перемещение материальной точки, скорость, характеризуются не
только своим числовым значением, но и направлением в пространстве. Такие физические величины называются векторными величинами (или коротко векторами)
8 Н
Слайд 13
Ненулевые векторы называются коллинеарными, если они лежат либо на
одной прямой, либо на параллельных прямых
Слайд 15
Если два ненулевых вектора коллинеарны и одинаково направлены, то
они называются сонаправленными
Слайд 17
Если два ненулевых вектора коллинеарны и направлены противоположно, то
они называются противоположно направленными
Слайд 23
С
А
В
D
4
3
M
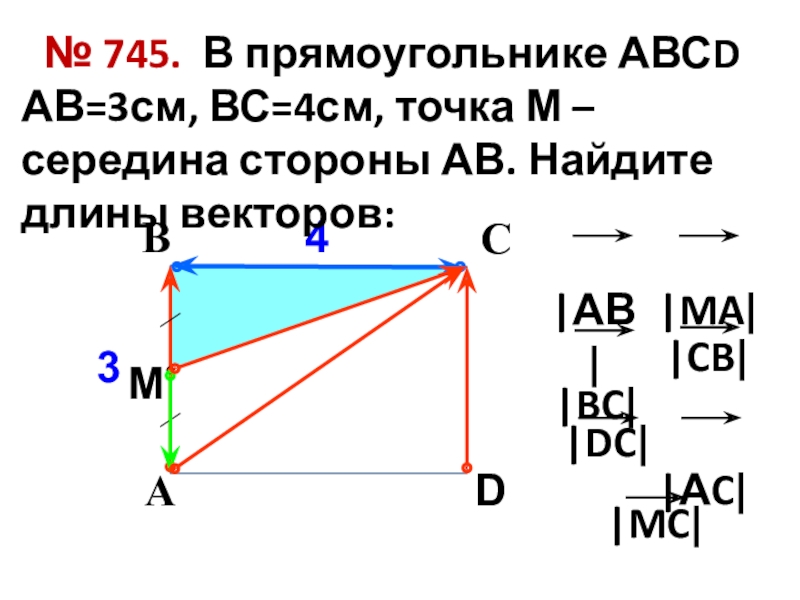
№ 745. В прямоугольнике АВСD АВ=3см, ВС=4см, точка
М – середина стороны АВ. Найдите длины векторов:
|MA|
|BC|
|CB|
|DC|
|MC|
|АВ|
|АC|
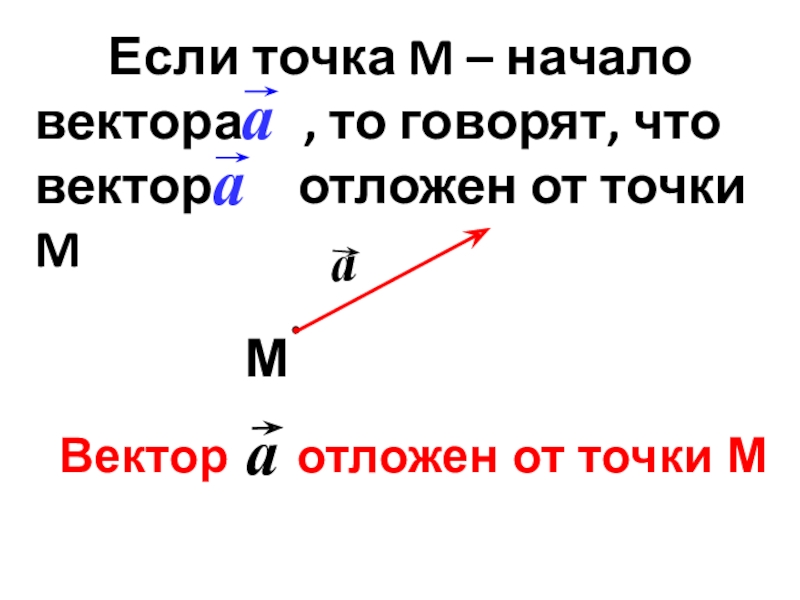
Слайд 25 Если точка M – начало вектора
, то говорят, что вектор отложен от точки M
Вектор отложен от точки M
a
Слайд 30 4. АВС – равнобедренный треугольник.
О – точка пересечения
медиан.
По данным рисунка найти
По данным рисунка найти
А
В
С
10
8
2
Слайд 33Список литературы
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия: Учебник
для 7-9 кл. средней школы. Москва, 2014 г.
Гаврилова Н.Ф. Поурочные разработки по геометрии: 9 класс.– М.: ВАКО, 2010. (В помощь школьному учителю).
Гаврилова Н.Ф. Поурочные разработки по геометрии: 9 класс.– М.: ВАКО, 2010. (В помощь школьному учителю).