ПЛОЩАДЬ ТРЕУГОЛЬНИКА ПЛОЩАДЬ
ТРАПЕЦИИ
Решение задач
Задание для самоподготовки:
П. 52, 53, 54 вопросы 4-8 стр. 133.
№ 467, 470, 478, 480(в).
№ 519*, 520*.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Площадь треугольника, площадь трапеции
Содержание
- 1. Презентация по геометрии на тему Площадь треугольника, площадь трапеции
- 2. «Если хотите научиться решать задачи, то
- 3. Устная работа №1. Площадь треугольника АВС равна
- 4. Площадь треугольника№ 2. Найдите площадь равнобедренного прямоугольного
- 5. №4. В ромбе из тупого угла, проведены
- 6. №6. Диагональ КР прямоугольника КМРТ равна 8
- 7. ПЛОЩАДЬ ТРЕУГОЛЬНИКАа1а2а3а4Равновеликими называются фигуры, которые имеют равные площадиа3 = а4
- 8. Систематизация знаний. . Отношениеn площадей треугольников
- 9. Развитие навыков решения задач на доказательствоСтороны прямоугольника
- 10. Развитие навыков решения задачСтороны параллелограмма а, b.
- 11. Площадь одного равностороннего треугольника в четыре раза
- 12. ПЛОЩАДЬ ТРАПЕЦИИ Задача 4824. Высота равнобедренной
- 13. ПЛОЩАДЬ ТРАПЕЦИИ (произвольной)Отрезок, соединяющий середины боковых сторон – средняя линия трапеции.S1S2bа
- 14. Площадь трапецииПлощадь трапеции равна произведению полусуммы
- 15. Свойства произвольной трапеции Определите площади ∆АВО
- 16. Решите задачуВ трапеции ABCD AB
- 17. Площадь трапецииВ прямоугольной трапеции площадь равна 30см2,
- 18. Площадь трапецииВ трапеции основания равны 20 и
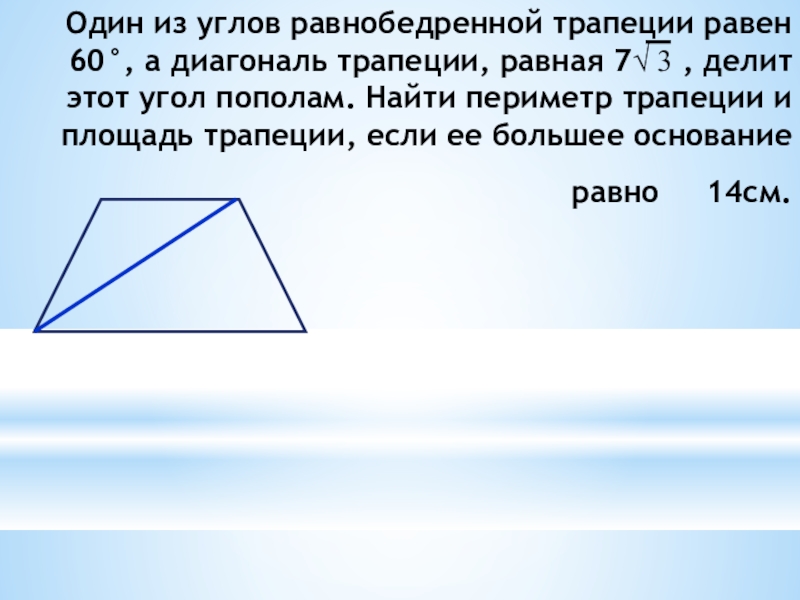
- 19. Один из углов равнобедренной трапеции равен 60°,
- 20. Площадь трапецииПериметр равнобедренной трапеции равен 64 см, боковая сторона 10см, площадь 88см2. Найдите высоту трапеции.
- 21. Свойство равнобедренной трапеции Если диагонали равнобедренной
- 22. Площадь равнобедренной трапеции, диагонали которой перпендикулярныЕсли
- 23. Площадь трапеции№ 518а, бПлощадь равнобокой трапеции со
- 24. Развитие навыков решения задач по теме «ПЛОЩАДИ»
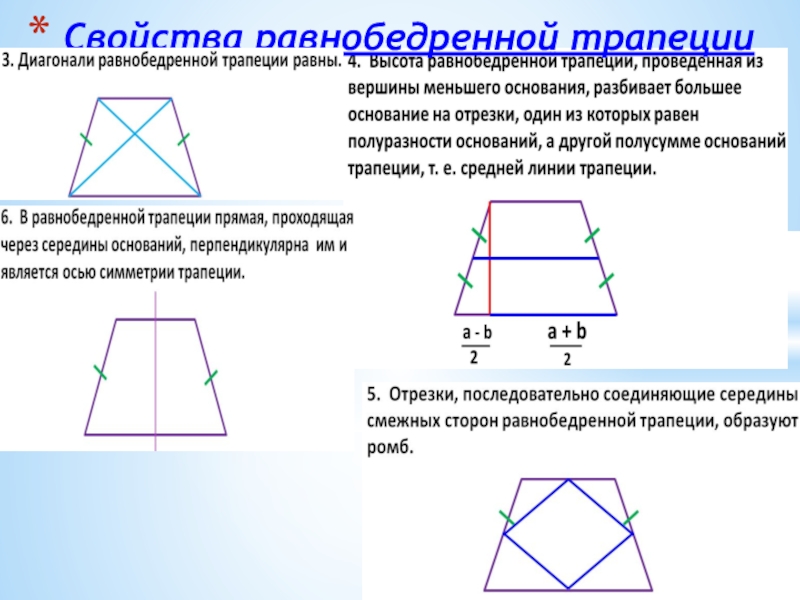
- 25. Свойства равнобедренной трапеции
- 26. КАК СВЯЗАНЫ ПЛОЩАДЬ РОМБА и ПЛОЩАДЬ
- 27. ПЛОЩАДЬ ТРАПЕЦИИ ЗадачаПлощадь трапеции равна произведению
- 28. ПЛОЩАДЬ ТРАПЕЦИИ ЗадачаПлощадь трапеции равна произведению
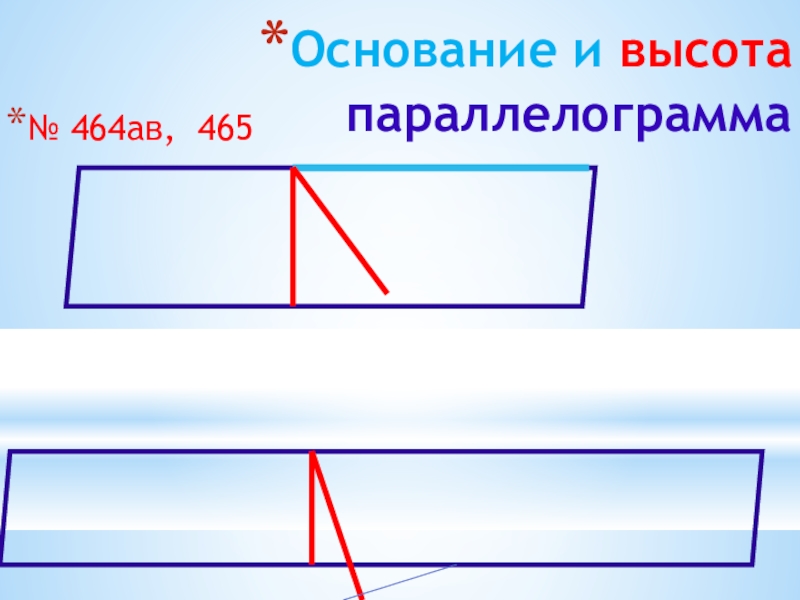
- 29. Основание и высота параллелограмма№ 464аб 465
- 30. Основание и высота параллелограмма№ 464ав, 465
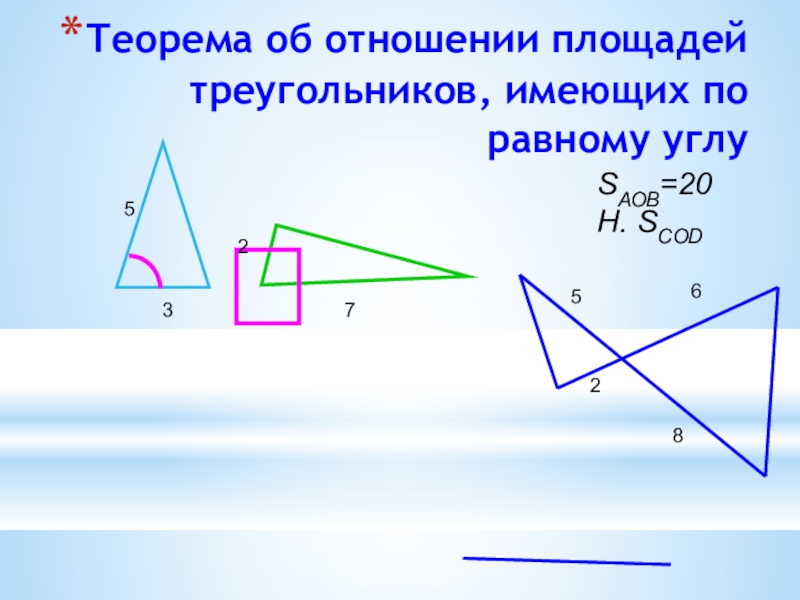
- 31. Теорема об отношении площадей треугольников, имеющих по равному углу53275628SАОВ=20Н. SСОD
- 32. Самостоятельна работаВариант 1. ДМ Ершова А.П.,стр.168 Вариант
- 33. Самостоятельна работаВариант 1.Вариант 2.Стороны параллелограмма равны 10
- 34. Самостоятельно
- 35. Итог урокаНазовите формулы, с помощью которых вычисляется:
- 36. Благодарю за урок55
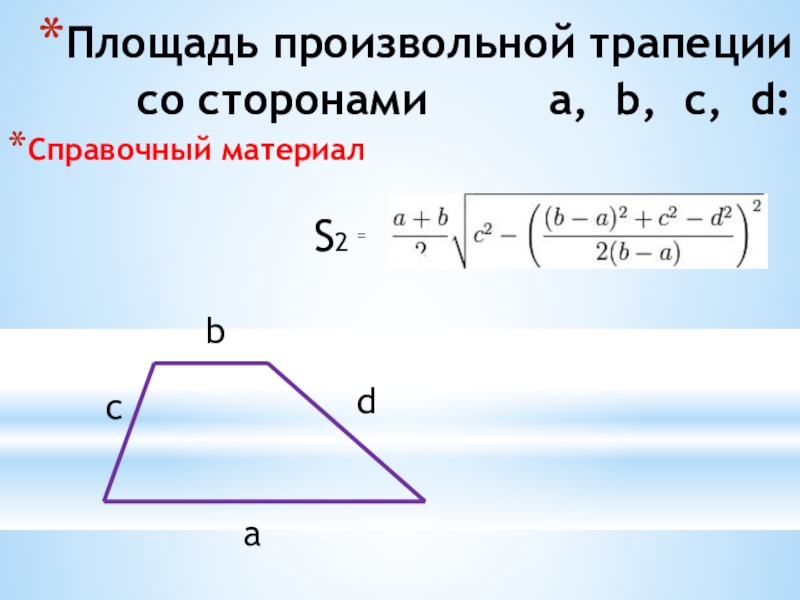
- 37. Площадь произвольной трапеции со сторонами
- 38. Свойства произвольной трапеции Справочный материал
«Если хотите научиться решать задачи, то решайте их» Дьердь Пойа Если вы хотите научиться плавать, то смело входите в воду,
Слайд 1У23 – 24
23.11.2016
Слайд 2
«Если хотите научиться решать задачи, то решайте их»
Дьердь Пойа
Если вы хотите научиться
плавать, то смело входите в воду,
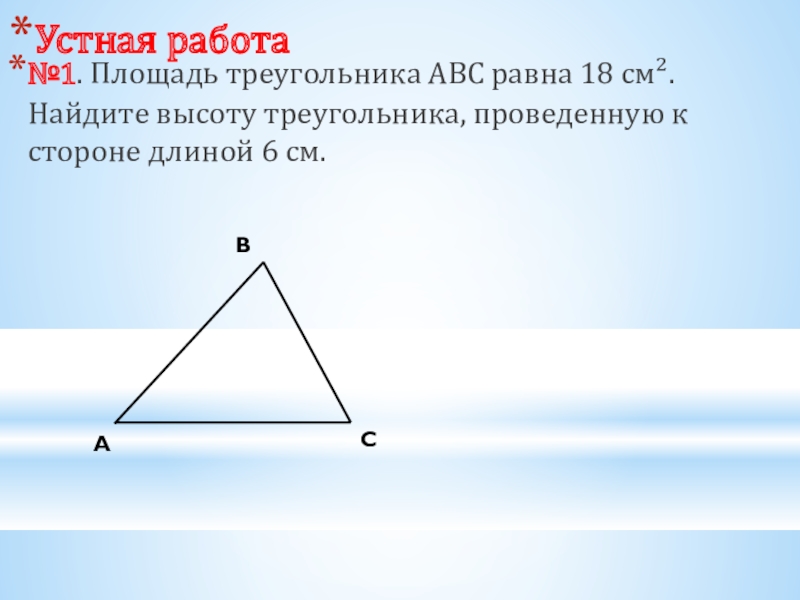
Слайд 3Устная работа
№1. Площадь треугольника АВС равна 18 см². Найдите высоту треугольника,
проведенную к стороне длиной 6 см.
A
C
B
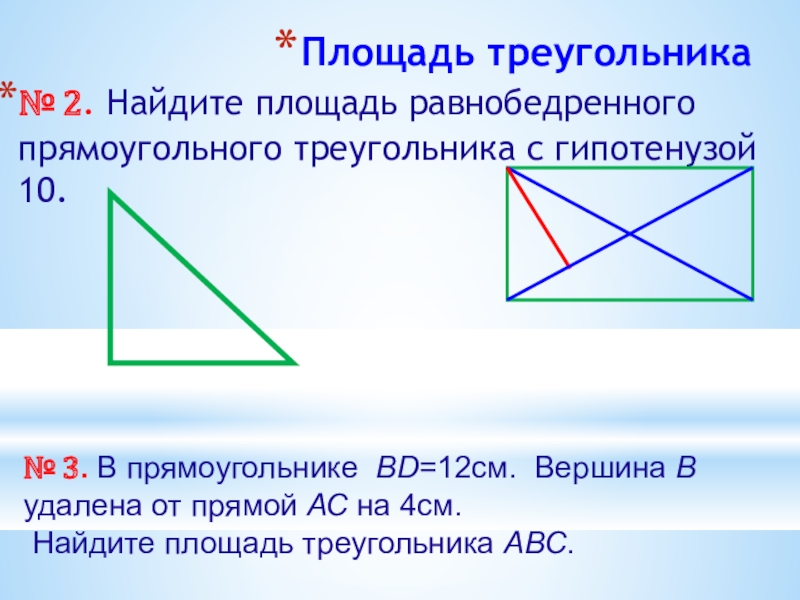
Слайд 4Площадь треугольника
№ 2. Найдите площадь равнобедренного прямоугольного треугольника с гипотенузой 10.
№
3. В прямоугольнике BD=12см. Вершина В удалена от прямой АС на 4см.
Найдите площадь треугольника АВС.
Найдите площадь треугольника АВС.
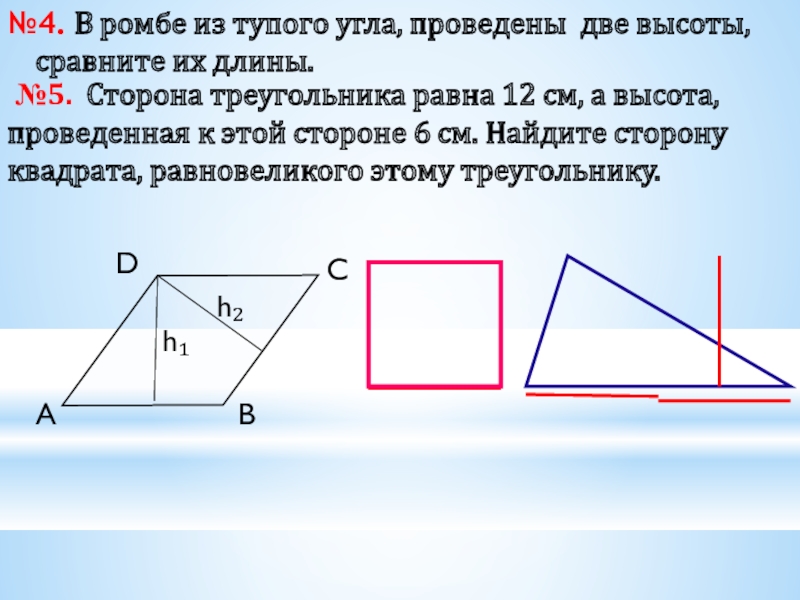
Слайд 5№4. В ромбе из тупого угла, проведены две высоты, сравните их
длины.
D
C
B
A
h₂
h₁
№5. Сторона треугольника равна 12 см, а высота, проведенная к этой стороне 6 см. Найдите сторону квадрата, равновеликого этому треугольнику.
Слайд 6
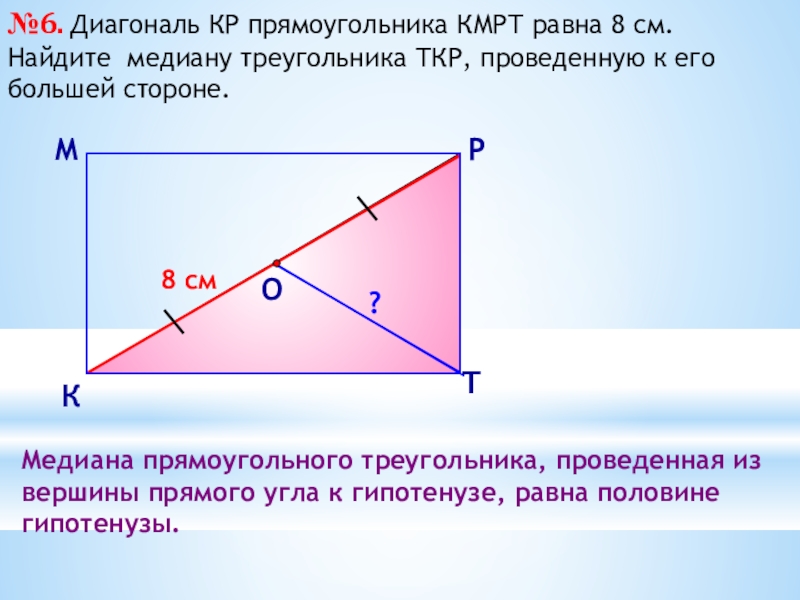
№6. Диагональ КР прямоугольника КМРТ равна 8 см. Найдите медиану треугольника
ТКР, проведенную к его большей стороне.
М
К
Р
Т
8 см
Медиана прямоугольного треугольника, проведенная из вершины прямого угла к гипотенузе, равна половине гипотенузы.
?
Слайд 7ПЛОЩАДЬ ТРЕУГОЛЬНИКА
а1
а2
а3
а4
Равновеликими называются фигуры, которые имеют равные площади
а3 = а4
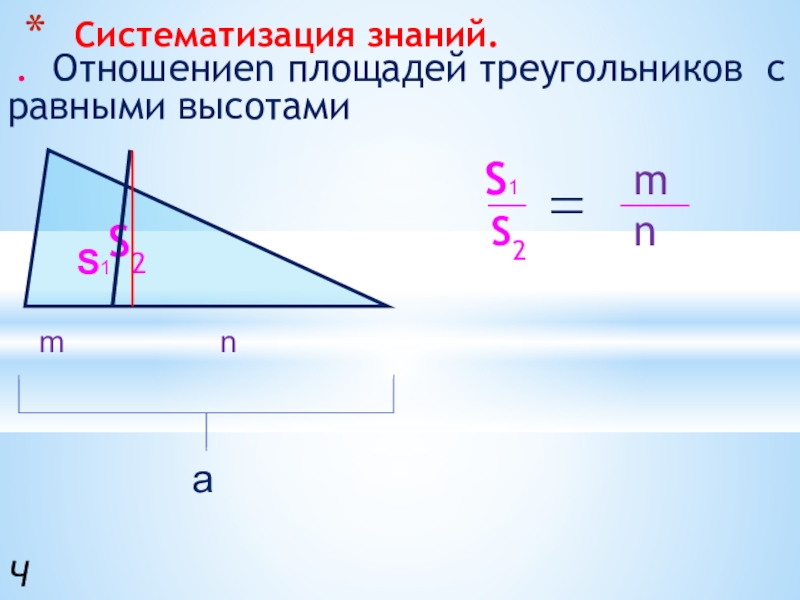
Слайд 8 Систематизация знаний.
. Отношениеn площадей треугольников с равными высотами
S1 m
S2 n
S2
S1
m n
a
Ч
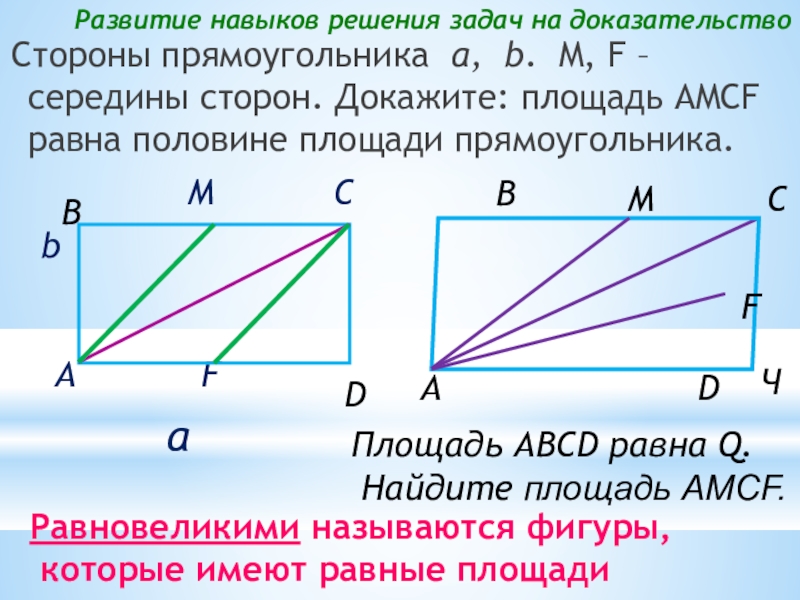
Слайд 9Развитие навыков решения задач на доказательство
Стороны прямоугольника a, b. M, F
– середины сторон. Докажите: площадь AMCF равна половине площади прямоугольника.
M C
b
A F
a
M C
b
A F
a
B
D
A
C
B
D
M
F
Площадь ABCD равна Q.
Найдите площадь AMCF.
Равновеликими называются фигуры,
которые имеют равные площади
Ч
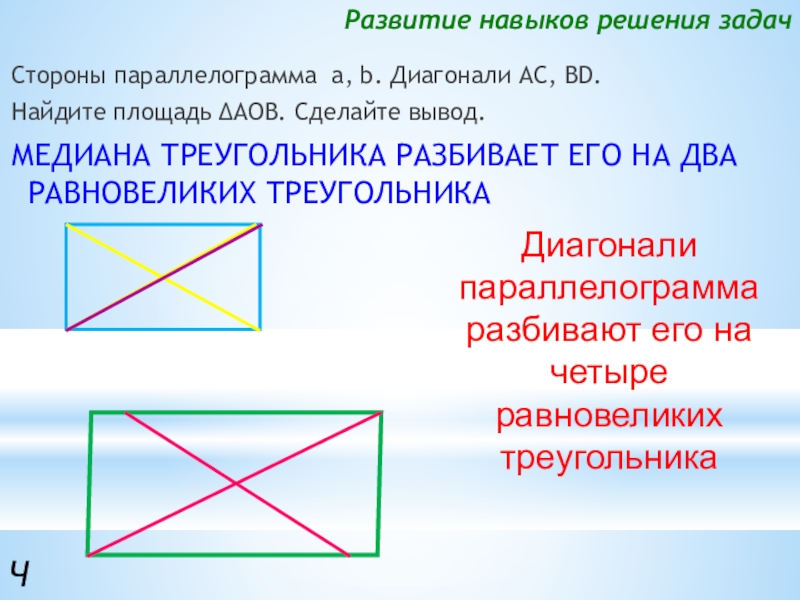
Слайд 10Развитие навыков решения задач
Стороны параллелограмма а, b. Диагонали AC, BD.
Найдите площадь
∆AOB. Cделайте вывод.
МЕДИАНА ТРЕУГОЛЬНИКА РАЗБИВАЕТ ЕГО НА ДВА РАВНОВЕЛИКИХ ТРЕУГОЛЬНИКА
МЕДИАНА ТРЕУГОЛЬНИКА РАЗБИВАЕТ ЕГО НА ДВА РАВНОВЕЛИКИХ ТРЕУГОЛЬНИКА
Диагонали параллелограмма
разбивают его на четыре равновеликих треугольника
Ч
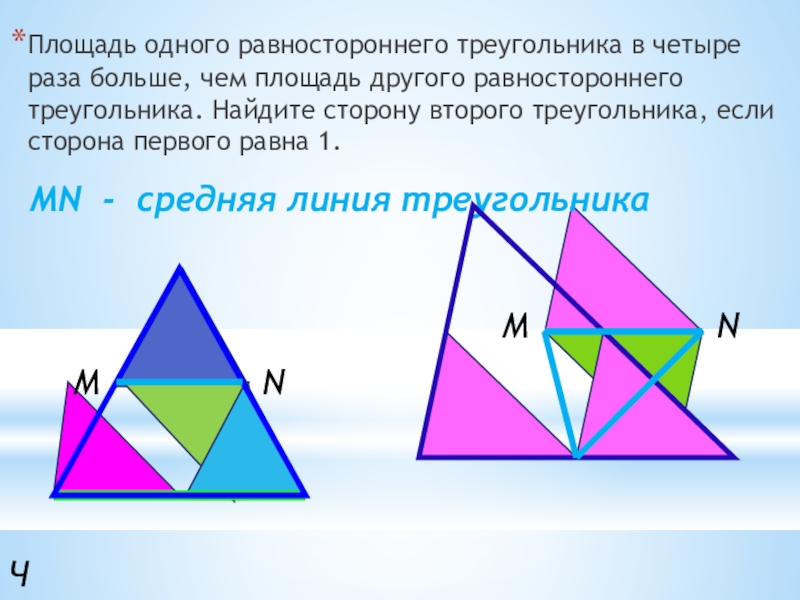
Слайд 11
Площадь одного равностороннего треугольника в четыре раза больше, чем площадь другого
равностороннего треугольника. Найдите сторону второго треугольника, если сторона первого равна 1.
М
N
МN - средняя линия треугольника
М
N
Ч
Слайд 12ПЛОЩАДЬ ТРАПЕЦИИ Задача 482
4. Высота равнобедренной трапеции, проведенная из вершины
меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.
a - b
2
а + b
2
Слайд 13ПЛОЩАДЬ ТРАПЕЦИИ
(произвольной)
Отрезок, соединяющий середины боковых сторон – средняя линия трапеции.
S1
S2
b
а
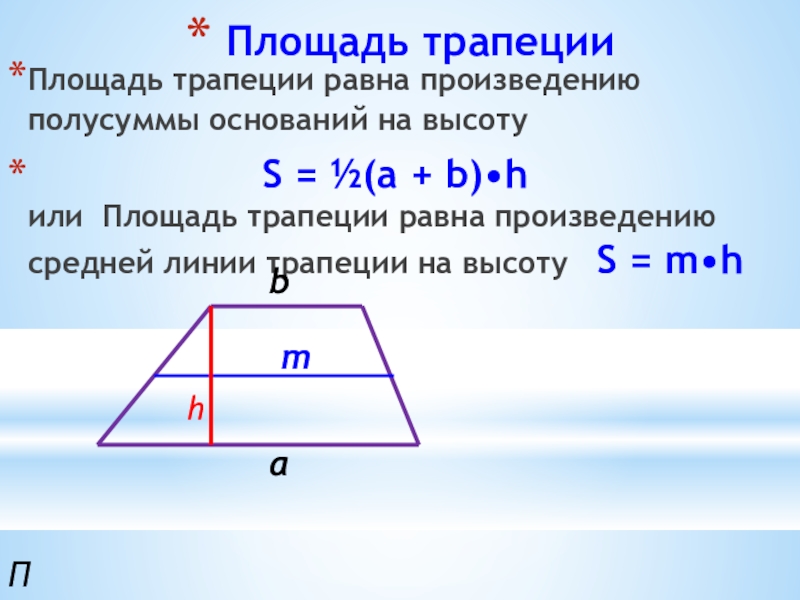
Слайд 14 Площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту
S = ½(a + b)•h или Площадь трапеции равна произведению средней линии трапеции на высоту S = m•h
h
b
a
m
П
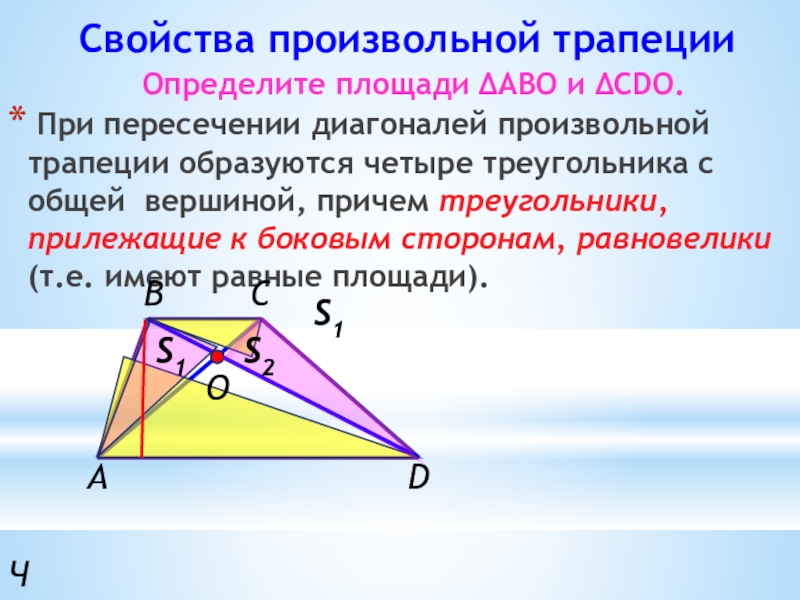
Слайд 15 Свойства произвольной трапеции
Определите площади ∆АВО и ∆CDO.
При пересечении диагоналей
произвольной трапеции образуются четыре треугольника с общей вершиной, причем треугольники, прилежащие к боковым сторонам, равновелики (т.е. имеют равные площади).
B
C
A
O
D
S1
S2
S1
Ч
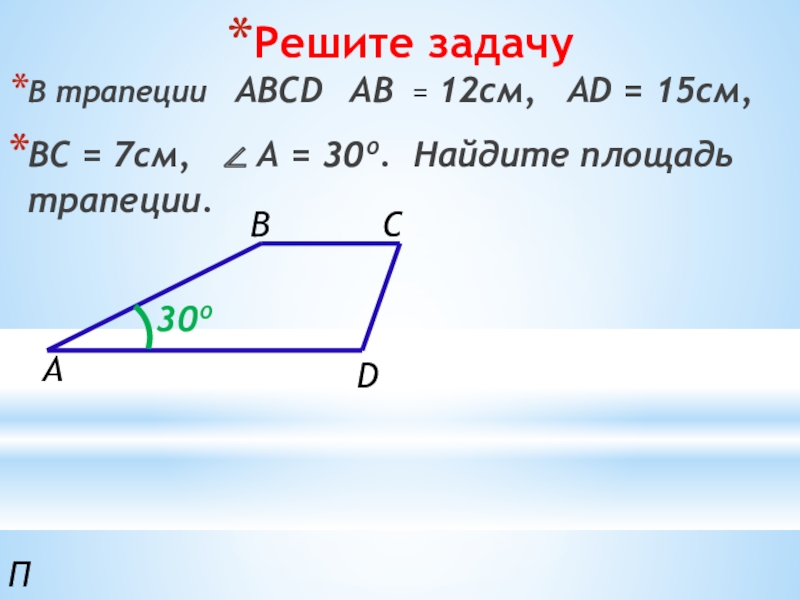
Слайд 16Решите задачу
В трапеции ABCD AB = 12см, AD
= 15см,
BC = 7см, ∠ А = 30º. Найдите площадь трапеции.
BC = 7см, ∠ А = 30º. Найдите площадь трапеции.
30º
D
А
В
С
П
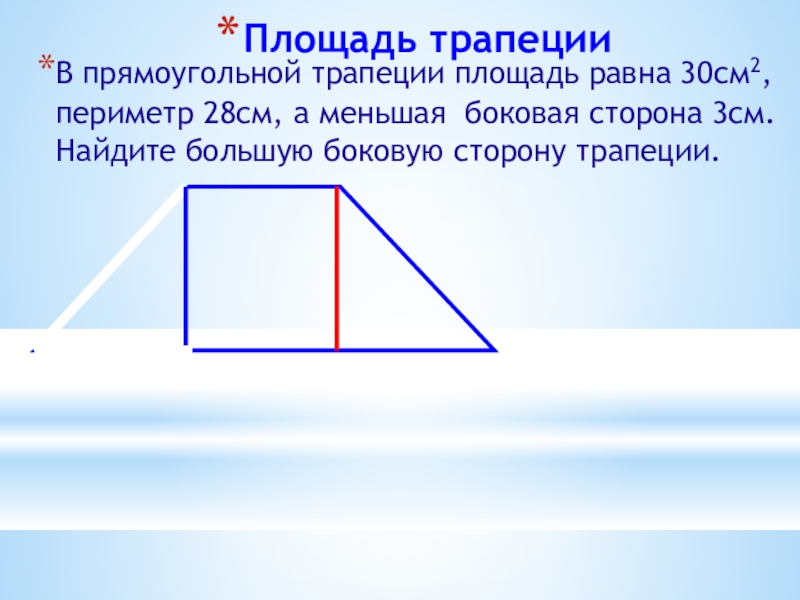
Слайд 17Площадь трапеции
В прямоугольной трапеции площадь равна 30см2, периметр 28см, а меньшая
боковая сторона 3см. Найдите большую боковую сторону трапеции.
№ 481
Слайд 18Площадь трапеции
В трапеции основания равны 20 и 16 см.
Площадь треугольника
с большим основанием равна 120см2. Найдите площадь трапеции.
Слайд 19Один из углов равнобедренной трапеции равен 60°, а диагональ трапеции, равная
7√ 3 , делит этот угол пополам. Найти периметр трапеции и площадь трапеции, если ее большее основание равно 14см.
Слайд 20Площадь трапеции
Периметр равнобедренной трапеции равен 64 см,
боковая сторона 10см, площадь
88см2. Найдите высоту трапеции.
Слайд 21 Свойство равнобедренной трапеции
Если диагонали равнобедренной трапеции перпендикулярны, то высота
трапеции равна
b
а
а
средней линии,
то есть полусумме оснований .
b
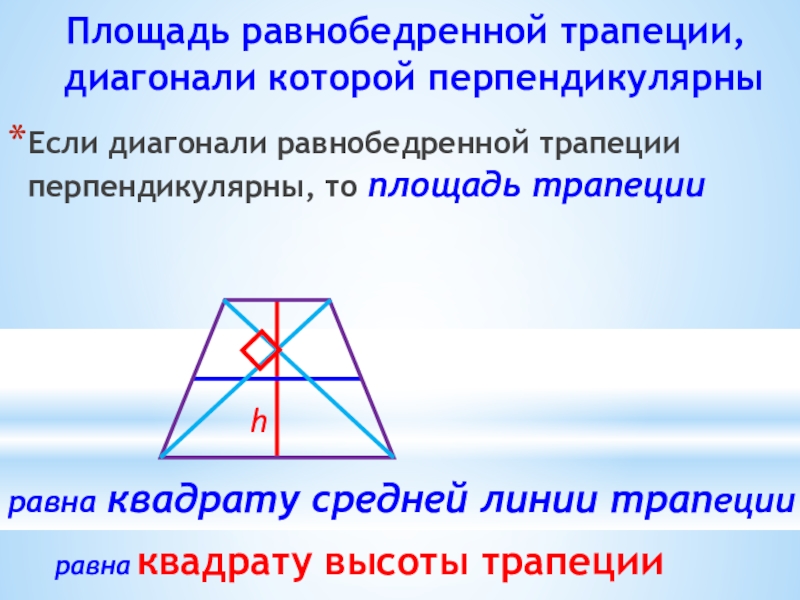
Слайд 22 Площадь равнобедренной трапеции, диагонали которой перпендикулярны
Если диагонали равнобедренной трапеции перпендикулярны,
то площадь трапеции
h
равна квадрату высоты трапеции
равна квадрату средней линии трапеции
Слайд 23Площадь трапеции
№ 518а, б
Площадь равнобокой трапеции со взаимно
перпендикулярными диагоналями равна
квадрату ее высоты или квадрату ее средней линии.
Высота равнобокой трапеции со взаимно
перпендикулярными диагоналями
равна ее средней линии
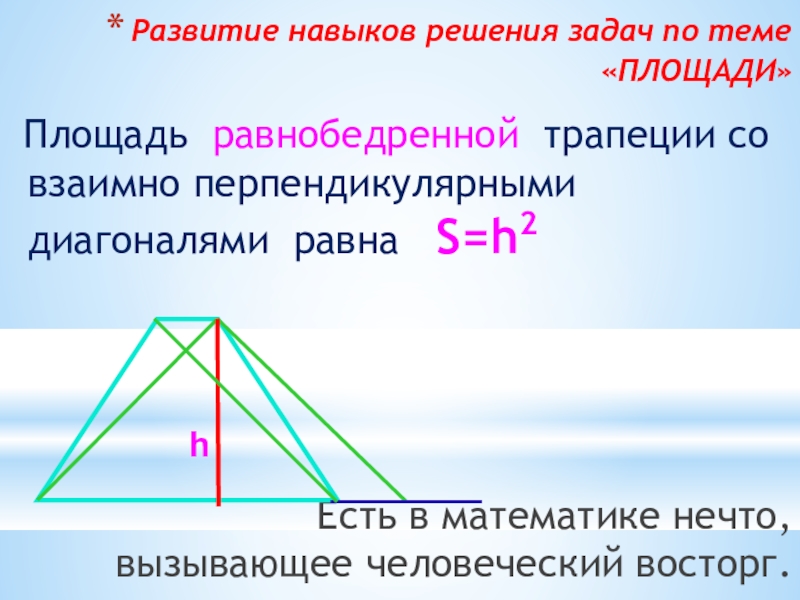
Слайд 24Развитие навыков решения задач по теме «ПЛОЩАДИ»
Площадь равнобедренной трапеции со
взаимно перпендикулярными диагоналями равна S=h2
Есть в математике нечто, вызывающее человеческий восторг.
Есть в математике нечто, вызывающее человеческий восторг.
h
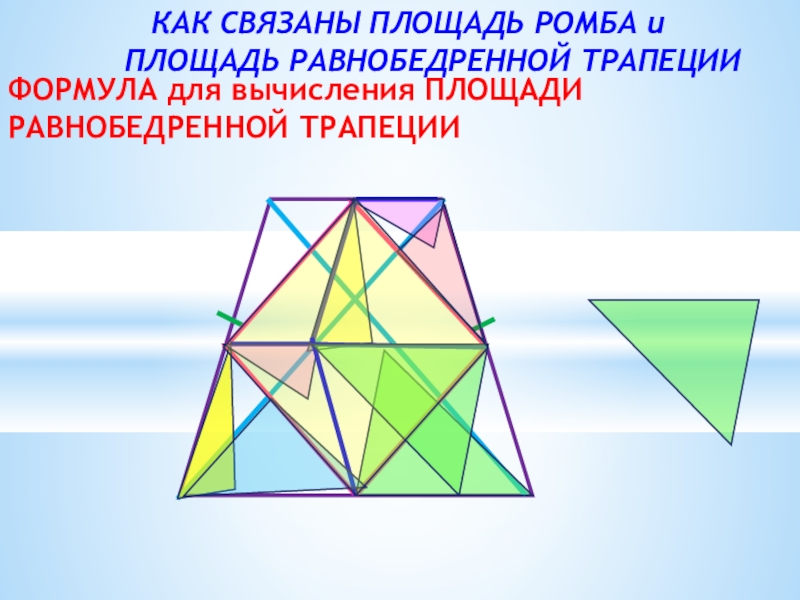
Слайд 26КАК СВЯЗАНЫ ПЛОЩАДЬ РОМБА и
ПЛОЩАДЬ РАВНОБЕДРЕННОЙ ТРАПЕЦИИ
ФОРМУЛА для вычисления ПЛОЩАДИ
РАВНОБЕДРЕННОЙ ТРАПЕЦИИ
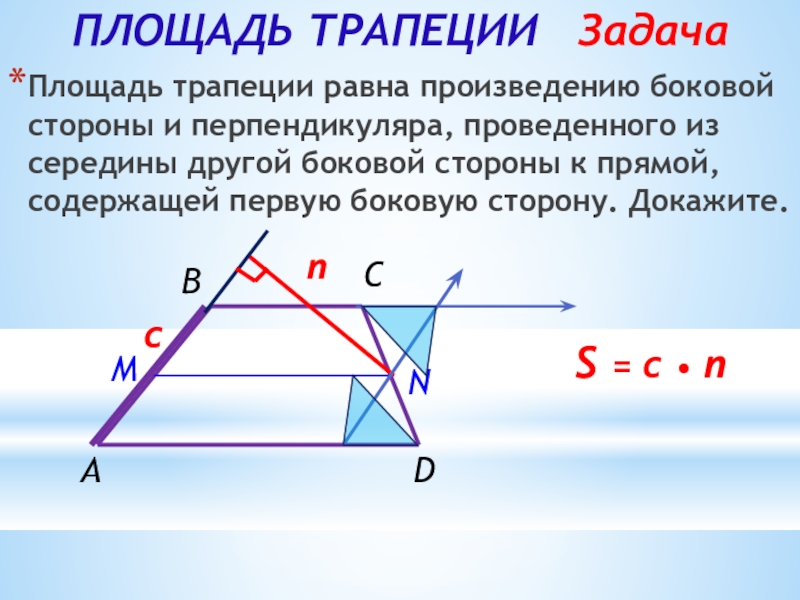
Слайд 27ПЛОЩАДЬ ТРАПЕЦИИ Задача
Площадь трапеции равна произведению боковой стороны и перпендикуляра,
проведенного из середины другой боковой стороны к прямой, содержащей первую боковую сторону. Докажите.
n
c
S = c • n
A
В
С
D
M
N
Слайд 28ПЛОЩАДЬ ТРАПЕЦИИ Задача
Площадь трапеции равна произведению боковой стороны и перпендикуляра,
проведенного из середины другой боковой стороны к прямой, содержащей первую боковую сторону. Докажите.
n
c
S = c • n
A
В
С
D
M
N
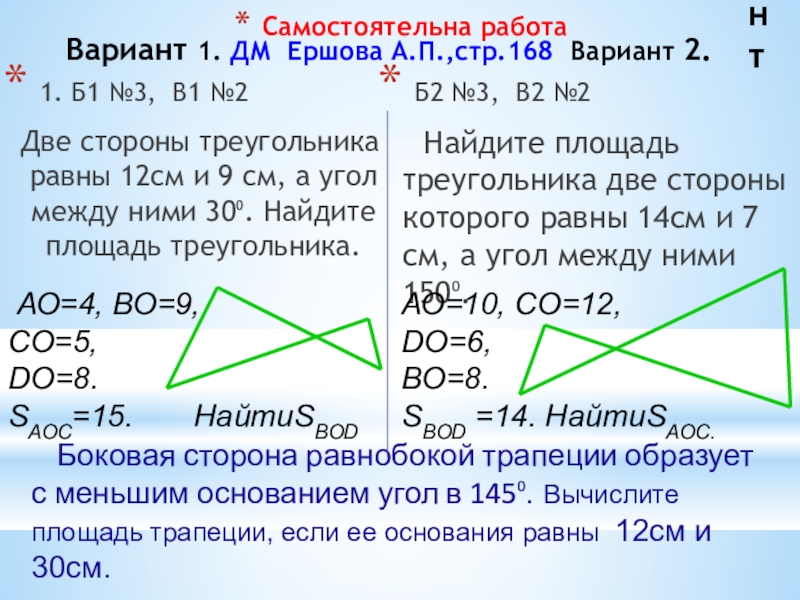
Слайд 32Самостоятельна работа
Вариант 1. ДМ Ершова А.П.,стр.168 Вариант 2.
Вариант
1. Б1
№3, В1 №2
Две стороны треугольника равны 12см и 9 см, а угол между ними 30⁰. Найдите площадь треугольника.
Две стороны треугольника равны 12см и 9 см, а угол между ними 30⁰. Найдите площадь треугольника.
Б2 №3, В2 №2
Найдите площадь треугольника две стороны которого равны 14см и 7 см, а угол между ними 150⁰.
Боковая сторона равнобокой трапеции образует с меньшим основанием угол в 145⁰. Вычислите площадь трапеции, если ее основания равны 12см и 30см.
АО=4, ВО=9,
СО=5,
DО=8.
SАОС=15. НайтиSВОD
АО=10, СО=12,
DО=6,
ВО=8.
SВОD =14. НайтиSАОС.
Слайд 33Самостоятельна работа
Вариант 1.
Вариант 2.
Стороны параллелограмма равны 10 и 6 см, а
угол между этими сторонами равен 150⁰. Найдите площадь этого параллелограмма.
Тупой угол параллелограмма равен 150⁰, а высоты проведенные из вершины этого угла равны 3 и 4 см. Найдите площадь этого параллелограмма.
Найдите площадь ромба, диагонали которого равны
6 см и 18 см. 14 см и 7 см.
Боковая сторона равнобокой трапеции, равная 20см, образует с меньшим основанием угол в 145⁰. Вычислите площадь трапеции, если ее основания равны 12см и 30см.
Слайд 35Итог урока
Назовите формулы, с помощью которых вычисляется:
ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА
ПЛОЩАДЬ ТРЕУГОЛЬНИКА
ПЛОЩАДЬ ТРАПЕЦИИ
Какие
новые свойства и формулы узнали на уроке?
Слайд 38 Свойства произвольной трапеции
Справочный материал
4. При пересечении диагоналей произвольной трапеции образуются
четыре треугольника с общей вершиной, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики(т.е. имеют равные площади).
