: «Пирамида»
учителя математики
ГБОУ СОШ №1056
Романенко Елены Алексеевны
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Пирамида
Содержание
- 1. Презентация по геометрии на тему Пирамида
- 2. ACDEHBSВершинаРёбраОснованиеOВысота пирамидыВысота боковой грани Боковая
- 3. Виды пирамид
- 4. Пирамида называется правильной, если основанием её является
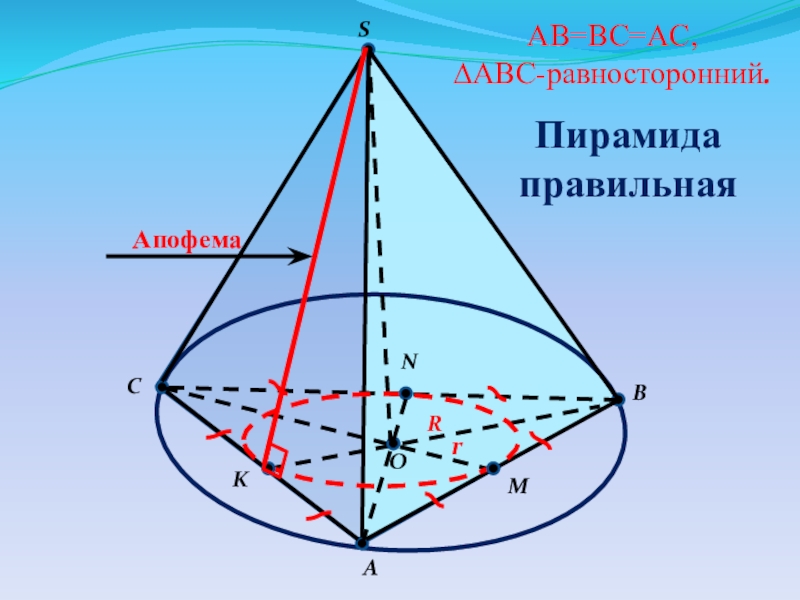
- 5. CBASOMNKAB=BC=AC,∆ABC-равносторонний.ПирамидаправильнаяrRАпофема
- 6. PO( катет) – общий;Все боковые рёбра правильной
- 7. PA2A3=…=PA1A2=Все боковые грани правильной пирамиды – равные
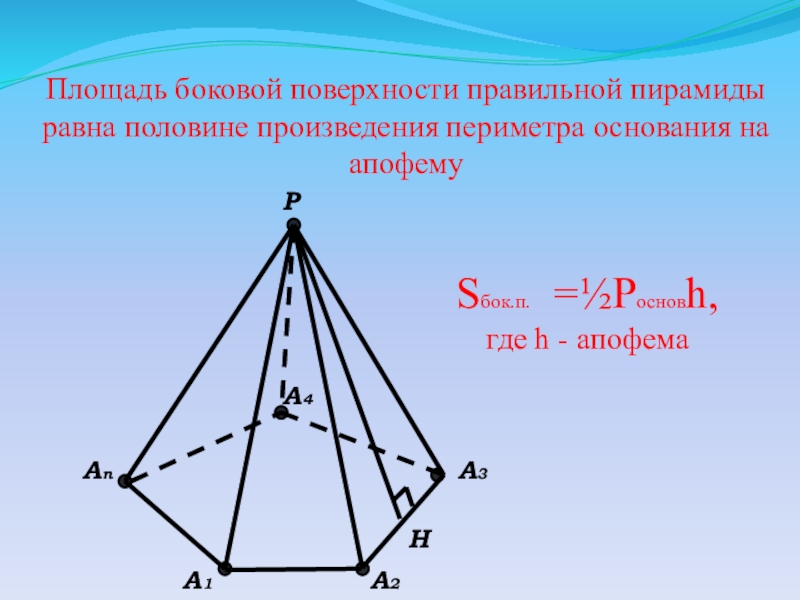
- 8. Площадь боковой поверхности правильной пирамиды равна половине
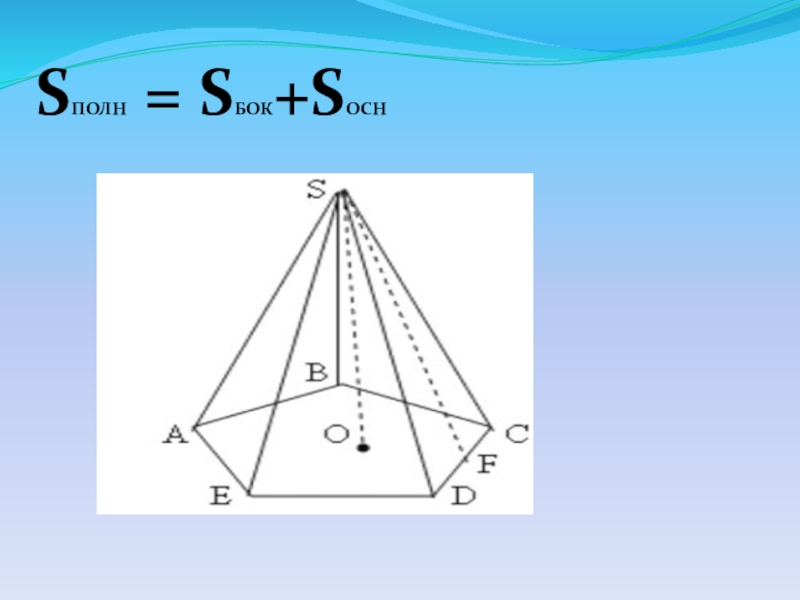
- 9. SПОЛН = SБОК+SОСН
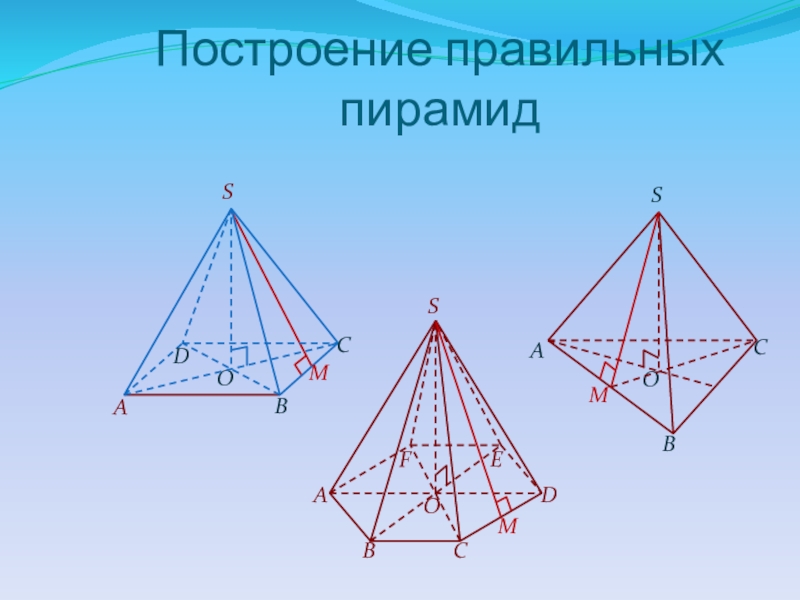
- 10. Построение правильных пирамид
- 11. УСЕЧЕННАЯ ПИРАМИДАПлоскость параллельная основанию пирамиды, разбивает её
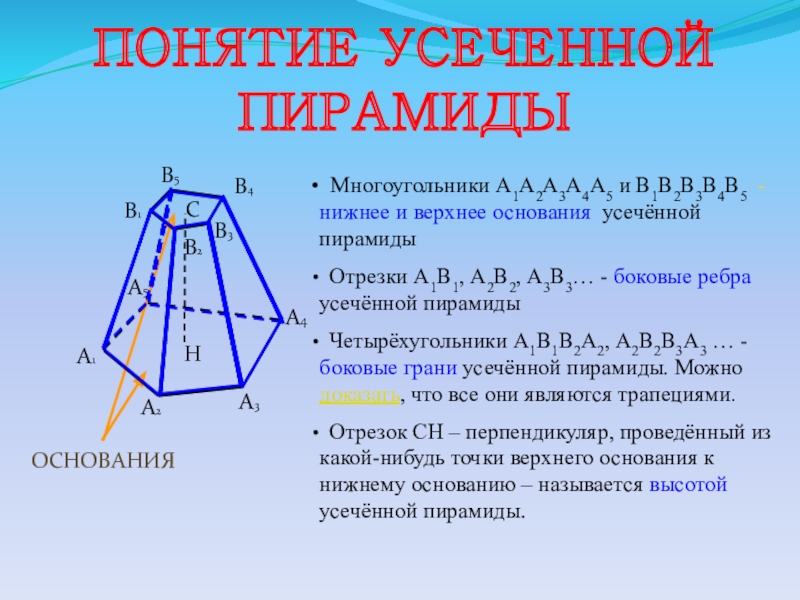
- 12. ПОНЯТИЕ УСЕЧЕННОЙ ПИРАМИДЫОСНОВАНИЯСН Многоугольники А1А2А3А4А5 и В1В2В3В4В5
- 13. ПРАВИЛЬНАЯ УСЕЧЕННАЯ ПИРАМИДА Усеченная пирамида называется правильной,
- 14. Правильным многоугольником называется многоугольник, у которого все
- 15. УСЕЧЕННЫЕ ПИРАМИДЫ
- 16. Усеченная четырехугольная пирамидаВАСО1A1C1D1B1DОАпофема Верхнее основание Нижнее основаниеБоковые грани(трапеции)
- 17. Площадью полной поверхности пирамиды (Sполн) пирамиды
- 18. Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.h
- 19. Объем пирамиды
- 20. Объем усеченной пирамидыВАСО1A1C1D1B1DО
- 21. Задача №1Дано: SABCD – пирамида, SB⊥ABCDABCD – квадрат, АВ = 2, ∠SAB = 60°.Найдите: Sбок.
- 22. Задача №2Дано: SABCD – пирамида, ABCD –
- 23. Задача №3Дано: SABCD – пирамида, ABCD –
- 24. № 255 В правильной треугольной пирамиде сторона
ACDEHBSВершинаРёбраОснованиеOВысота пирамидыВысота боковой грани Боковая граньПирамида (др. греч. πυραμίς) – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину
Слайд 1Департамент образования города Москвы
Северо-Западное окружное управление образования
Презентация по геометрии на тему
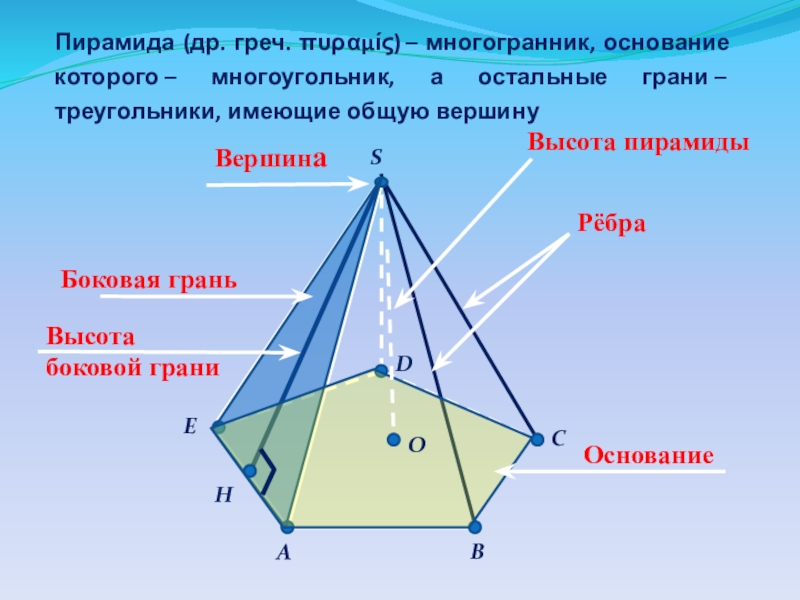
Слайд 2A
C
D
E
H
B
S
Вершина
Рёбра
Основание
O
Высота пирамиды
Высота боковой грани
Боковая грань
Пирамида (др. греч. πυραμίς) –
многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину
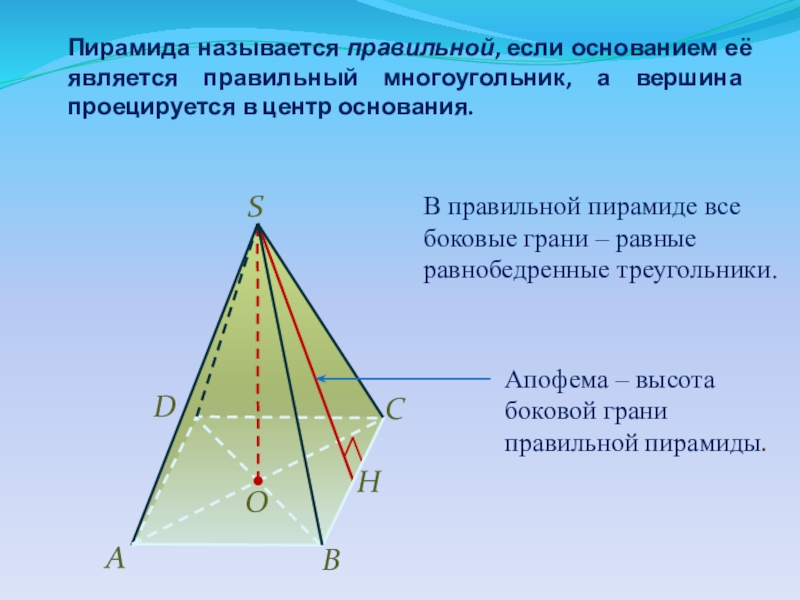
Слайд 4Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина
проецируется в центр основания.
В правильной пирамиде все боковые грани – равные равнобедренные треугольники.
Апофема – высота боковой грани правильной пирамиды.
Слайд 6PO( катет) – общий;
Все боковые рёбра правильной пирамиды равны.
P
A2
An
A1
PA1A2…An - правильная
пирамида
O
h
R
R
OPA1 =
OPA2 = …
2.OA1=OA2=…R
(катеты)
Значит,
PA1=PA2 =…
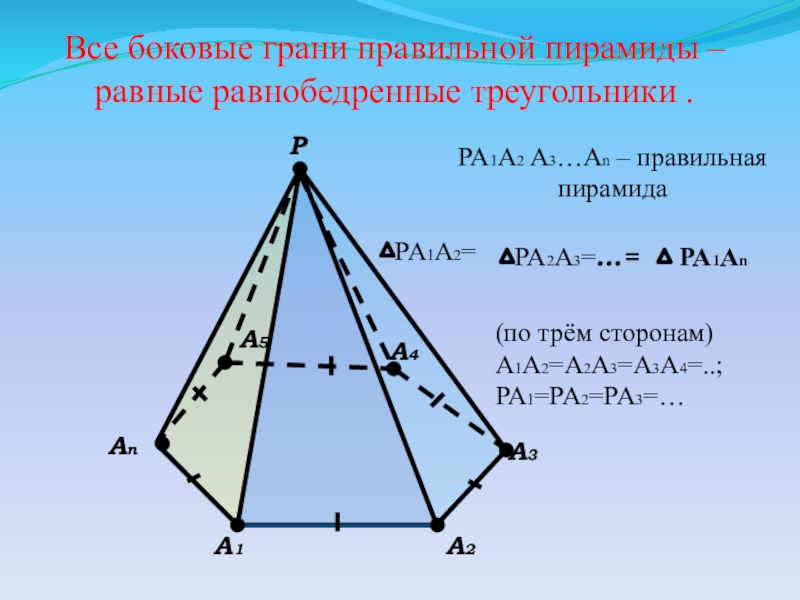
Слайд 7PA2A3=…=
PA1A2=
Все боковые грани правильной пирамиды – равные равнобедренные треугольники .
A1
A2
A3
A4
A5
An
P
PA1A2 A3…An
– правильная пирамида
PA1An
(по трём сторонам)
A1A2=A2A3=A3A4=..;
PA1=PA2=PA3=…
Слайд 8Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на
апофему
A1
A2
A3
A4
An
P
H
Sбок.п. =½Pосновh,
где h - апофема
Слайд 11УСЕЧЕННАЯ ПИРАМИДА
Плоскость параллельная основанию пирамиды, разбивает её на два многогранника. Один
из них является пирамидой, а другой называется усечённой пирамидой.
Усеченная пирамида – это часть полной пирамиды, заключенная между её основанием и секущей плоскостью, параллельной основанию данной пирамиды
Усеченная пирамида – это часть полной пирамиды, заключенная между её основанием и секущей плоскостью, параллельной основанию данной пирамиды
Слайд 12ПОНЯТИЕ УСЕЧЕННОЙ ПИРАМИДЫ
ОСНОВАНИЯ
С
Н
Многоугольники А1А2А3А4А5 и В1В2В3В4В5 - нижнее и верхнее
основания усечённой пирамиды
Отрезки А1В1, А2В2, А3В3… - боковые ребра усечённой пирамиды
Четырёхугольники А1В1В2А2, А2В2В3А3 … - боковые грани усечённой пирамиды. Можно доказать, что все они являются трапециями.
Отрезок СН – перпендикуляр, проведённый из какой-нибудь точки верхнего основания к нижнему основанию – называется высотой усечённой пирамиды.
Отрезки А1В1, А2В2, А3В3… - боковые ребра усечённой пирамиды
Четырёхугольники А1В1В2А2, А2В2В3А3 … - боковые грани усечённой пирамиды. Можно доказать, что все они являются трапециями.
Отрезок СН – перпендикуляр, проведённый из какой-нибудь точки верхнего основания к нижнему основанию – называется высотой усечённой пирамиды.
Слайд 13ПРАВИЛЬНАЯ УСЕЧЕННАЯ ПИРАМИДА
Усеченная пирамида называется правильной, если она получена сечением
правильной пирамиды плоскостью, параллельной основанию.
Основания - правильные многоугольники .
Боковые грани – равные равнобедренные трапеции.
Высоты этих трапеций называются апофемами.
Основания - правильные многоугольники .
Боковые грани – равные равнобедренные трапеции.
Высоты этих трапеций называются апофемами.
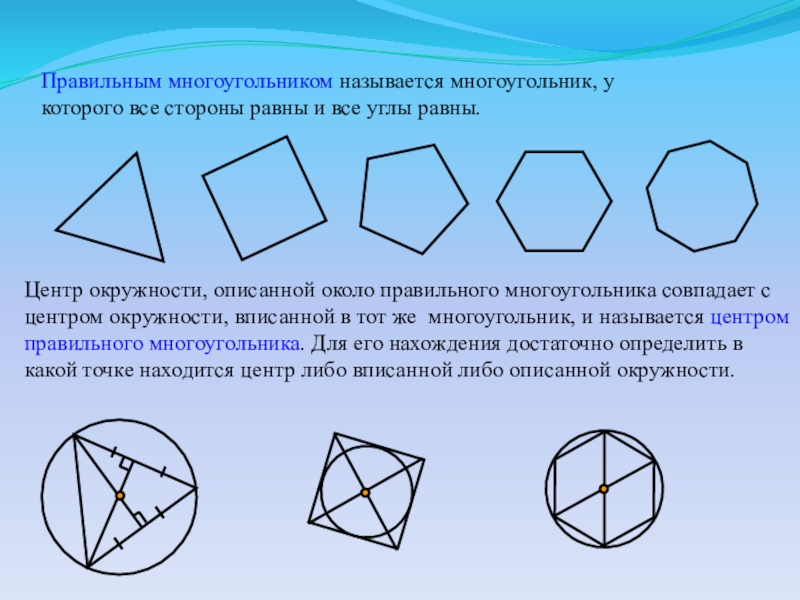
Слайд 14Правильным многоугольником называется многоугольник, у которого все стороны равны и все
углы равны.
Центр окружности, описанной около правильного многоугольника совпадает с центром окружности, вписанной в тот же многоугольник, и называется центром правильного многоугольника. Для его нахождения достаточно определить в какой точке находится центр либо вписанной либо описанной окружности.
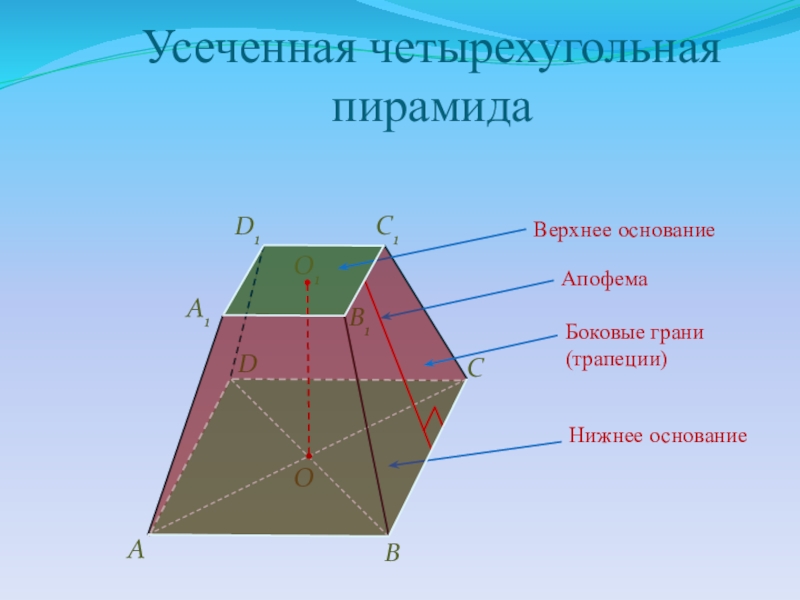
Слайд 16Усеченная четырехугольная пирамида
В
А
С
О1
A1
C1
D1
B1
D
О
Апофема
Верхнее основание
Нижнее основание
Боковые грани
(трапеции)
Слайд 17 Площадью полной поверхности пирамиды (Sполн) пирамиды называется сумма площадей всех
её граней: основания и всех боковых граней.
Sполн =Sбок+Sосн
Sполн.усеч .= Sбок + Sверхн.осн. + Sнижн.осн.
Площадью боковой поверхности (Sбок) пирамиды называется сумма площадей её боковых граней.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. (Доказательство на следующем слайде)
Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.
Sполн =Sбок+Sосн
Sполн.усеч .= Sбок + Sверхн.осн. + Sнижн.осн.
Площадью боковой поверхности (Sбок) пирамиды называется сумма площадей её боковых граней.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. (Доказательство на следующем слайде)
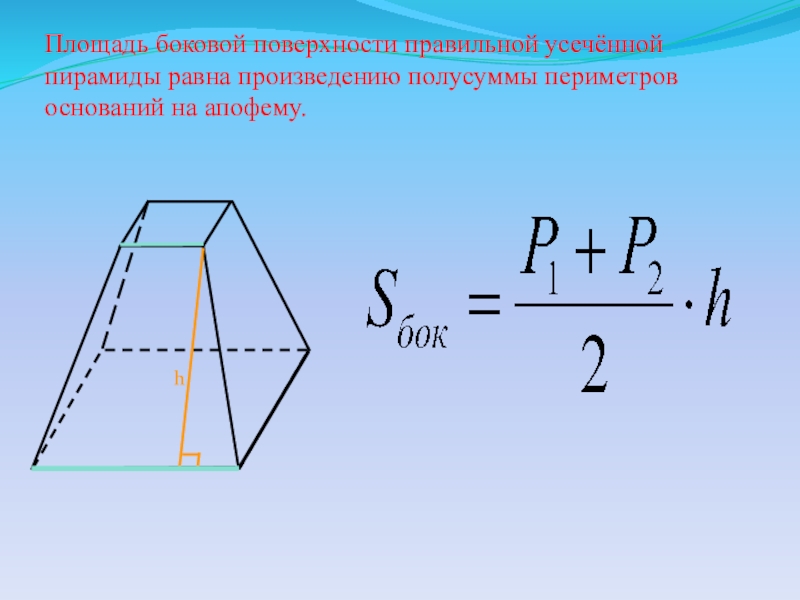
Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.
ПЛОЩАДЬ ПОВЕРХНОСТИ УСЕЧЁННОЙ ПИРАМИДЫ
Слайд 18Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований
на апофему.
h
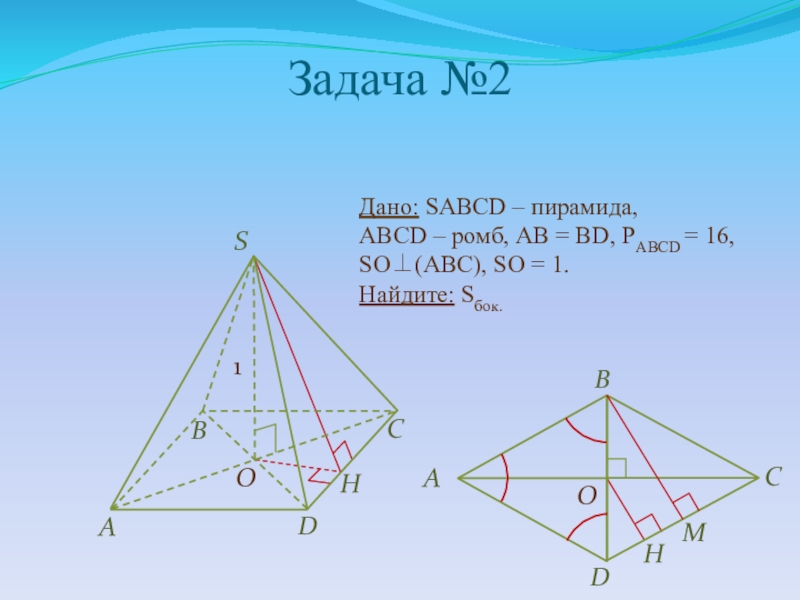
Слайд 22Задача №2
Дано: SABCD – пирамида,
ABCD – ромб, АВ = BD,
РABCD = 16,
SO⊥(АВС), SO = 1.
Найдите: Sбок.
SO⊥(АВС), SO = 1.
Найдите: Sбок.
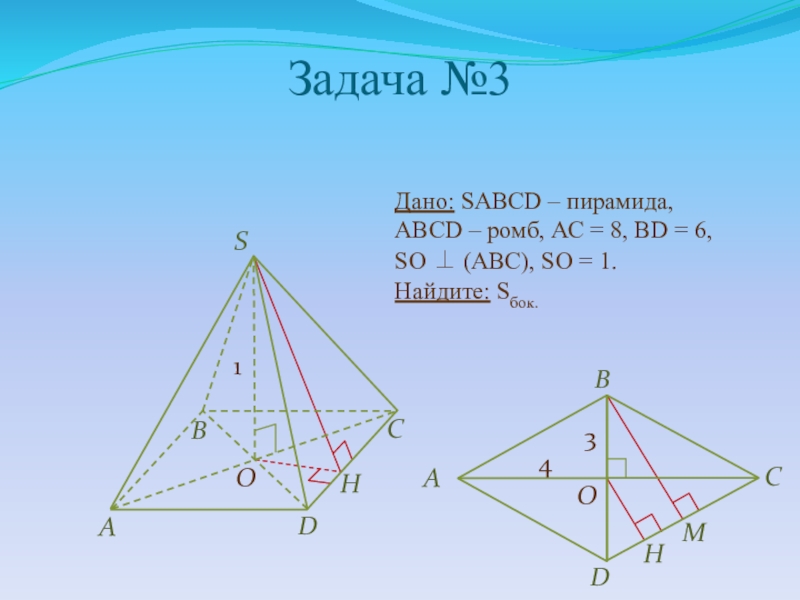
Слайд 23Задача №3
Дано: SABCD – пирамида,
ABCD – ромб, АС = 8,
BD = 6,
SO ⊥ (АВС), SO = 1.
Найдите: Sбок.
SO ⊥ (АВС), SO = 1.
Найдите: Sбок.
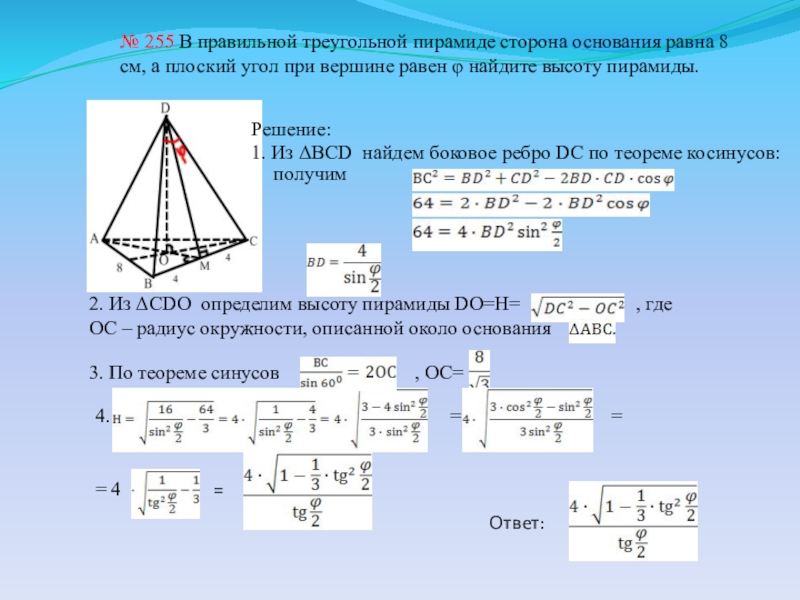
Слайд 24№ 255 В правильной треугольной пирамиде сторона основания равна 8 см,
а плоский угол при вершине равен φ найдите высоту пирамиды.
Решение:
1. Из ΔBCD найдем боковое ребро DC по теореме косинусов:
получим
2. Из ΔCDO определим высоту пирамиды DO=H= , где ОС – радиус окружности, описанной около основания
3. По теореме синусов , ОС=
4. = =
= 4 =
Ответ:
