- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Первый признак подобия треугольников
Содержание
- 1. Презентация по геометрии на тему Первый признак подобия треугольников
- 2. 1. Какие треугольники называются подобными?2. Какие стороны
- 3. АВСС1В1А1Задача Дано: 7см6смНайдите: х, у, z. хz40см8смy30см35см
- 4. N32МДоказать: Верно6481624F8106008103903906002) Доказать пропорциональность сходственных сторон.1) Доказать равенство углов.?
- 5. Сформулировать теорему об отношении площадей треугольников, имеющих по равному углу.АВСА1В1С1
- 6. Если два угла одного треугольника соответственно равны
- 7. АВСА1В1С1Т.к. ∠А = ∠А1, ∠В = ∠В1, тоΔ АВС ~ Δ А1В1С1
- 8. АВСDО1. Дано: АВСD – трапеция, АС и ВD – диагонали.Найти подобные треугольники.Δ АОD ~ Δ ВОС
- 9. KLMFN△КМN, LF ∥KNНайти подобные треугольники∠М
- 10. Решить: № 551 (а)АВСDЕF84710??План решенияДоказать, что Δ
- 11. Домашнее задание:п. 59 (док-во теоремы), № 550, 552 (а)
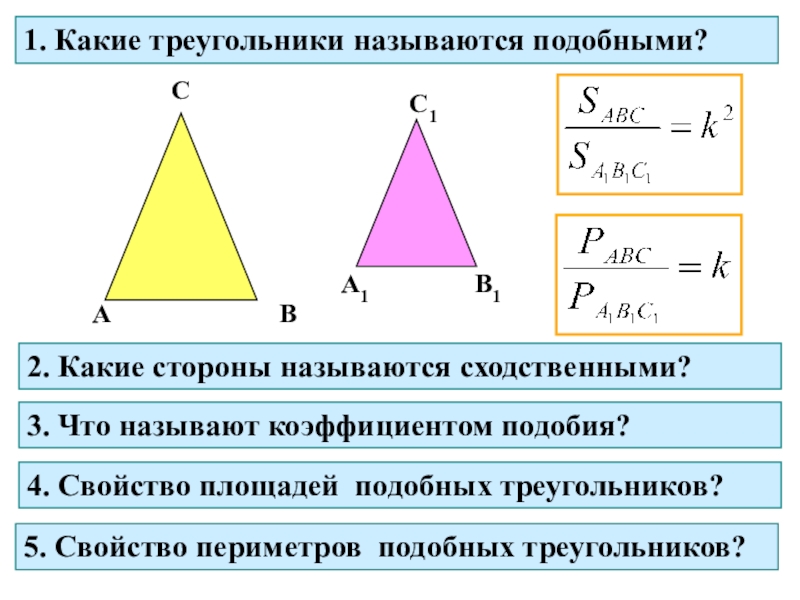
1. Какие треугольники называются подобными?2. Какие стороны называются сходственными?4. Свойство площадей подобных треугольников?5. Свойство периметров подобных треугольников?3. Что называют коэффициентом подобия?
Слайд 1Первый
признак
подобия
треугольников
Кретинина И.Л., учитель МОКУ Струговская ООШ Октябрьского района,
Приморского края
Слайд 21. Какие треугольники называются подобными?
2. Какие стороны называются сходственными?
4. Свойство площадей
подобных треугольников?
5. Свойство периметров подобных треугольников?
3. Что называют коэффициентом подобия?
Слайд 4
N
32
М
Доказать:
Верно
6
4
8
16
24
F
810
600
810
390
390
600
2) Доказать пропорциональность
сходственных сторон.
1) Доказать равенство углов.
?
Слайд 5Сформулировать теорему об отношении площадей треугольников, имеющих по равному углу.
А
В
С
А1
В1
С1
Слайд 6Если два угла одного треугольника соответственно равны двум углам другого треугольника,
то такие треугольники подобны.
А
В
С
А1
В1
С1
Доказать: Δ АВС ~ Δ А1В1С1
Доказательство:
Т.к. ∠А = ∠А1, ∠С = ∠С1, то:
Итак, ∠А=∠А1, ∠В=∠В1, ∠С=∠С1.
Слайд 10Решить: № 551 (а)
А
В
С
D
Е
F
8
4
7
10
?
?
План решения
Доказать, что
Δ АЕD ~ Δ FЕС
2.
Найти сходственные стороны этих треугольников и коэффициент подобия
3. Найти ЕF и FC
3. Найти ЕF и FC
Ответ: FC = 3,5 см, FЕ = 5 см.