- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему: Параллелограмм (8класс)
Содержание
- 1. Презентация по геометрии на тему: Параллелограмм (8класс)
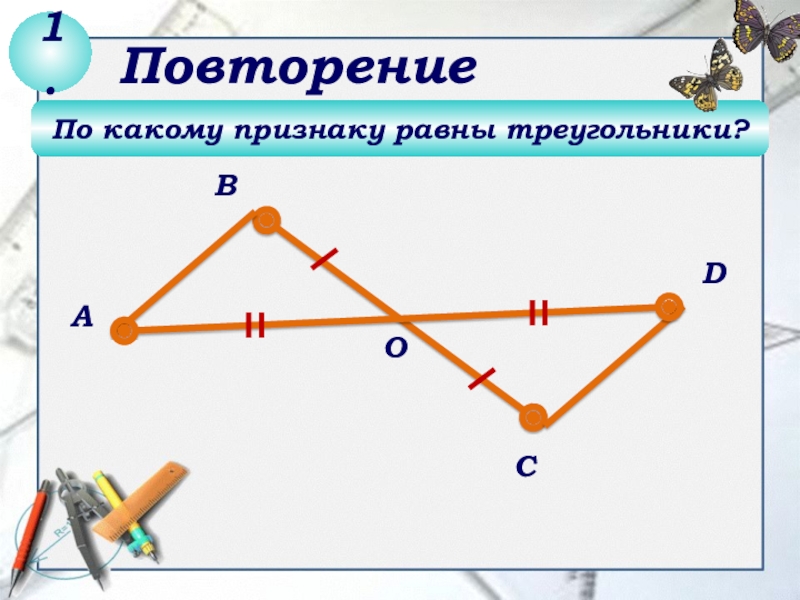
- 2. По какому признаку равны треугольники? DСВАО1.Повторение
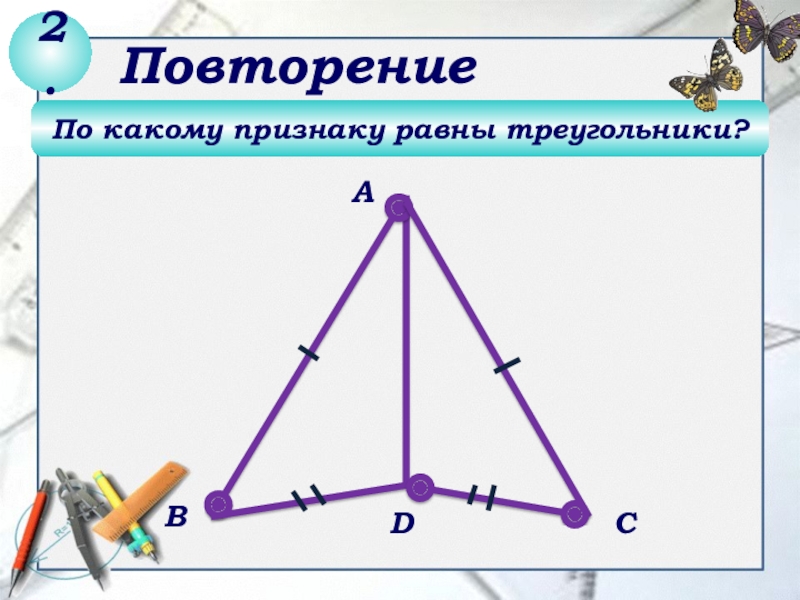
- 3. По какому признаку равны треугольники?DСВА2.Повторение
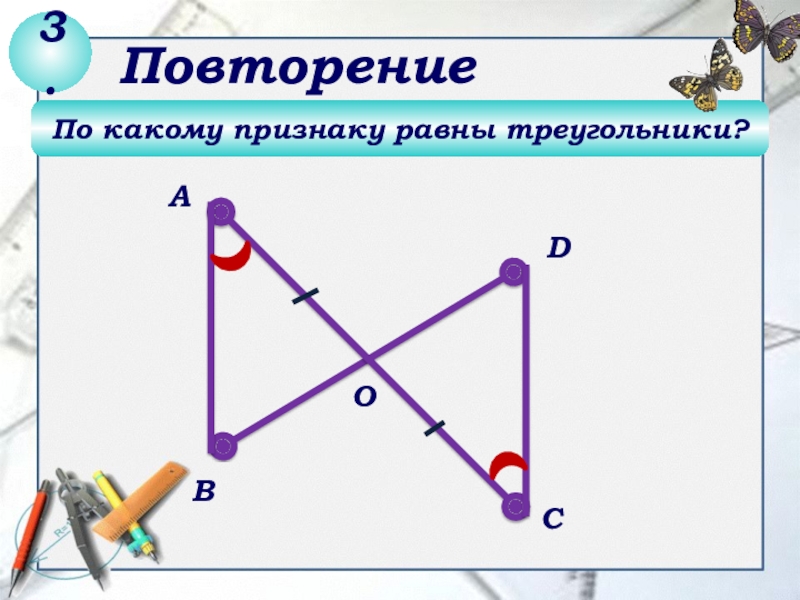
- 4. По какому признаку равны треугольники?DСВАО3.Повторение
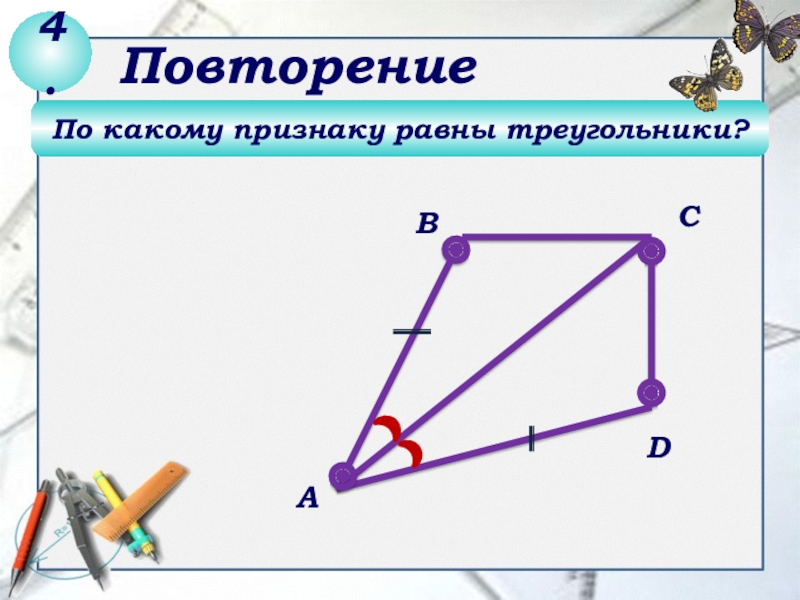
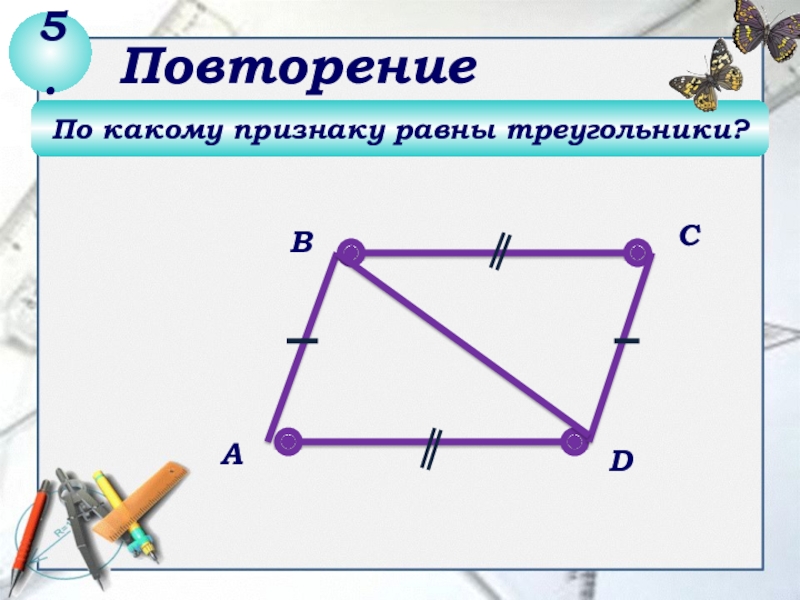
- 5. По какому признаку равны треугольники?DСВА4.Повторение
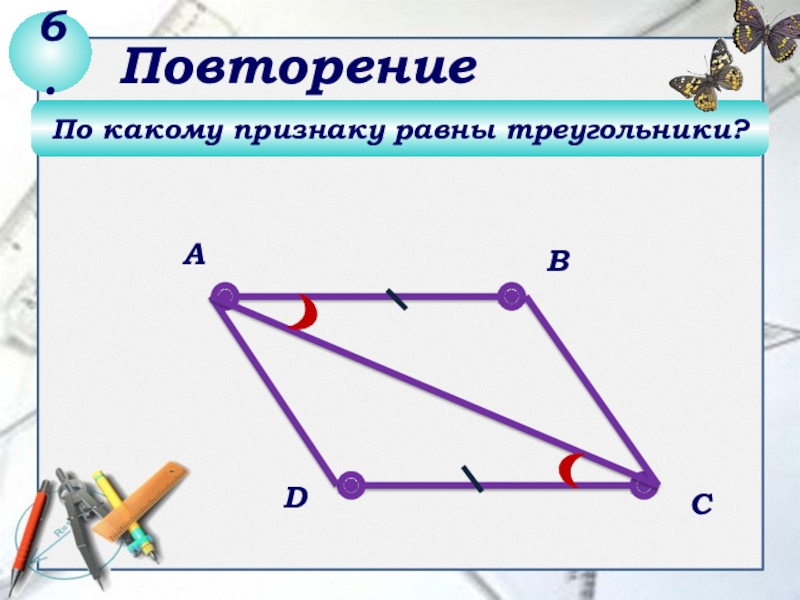
- 6. По какому признаку равны треугольники?DСВА5.Повторение
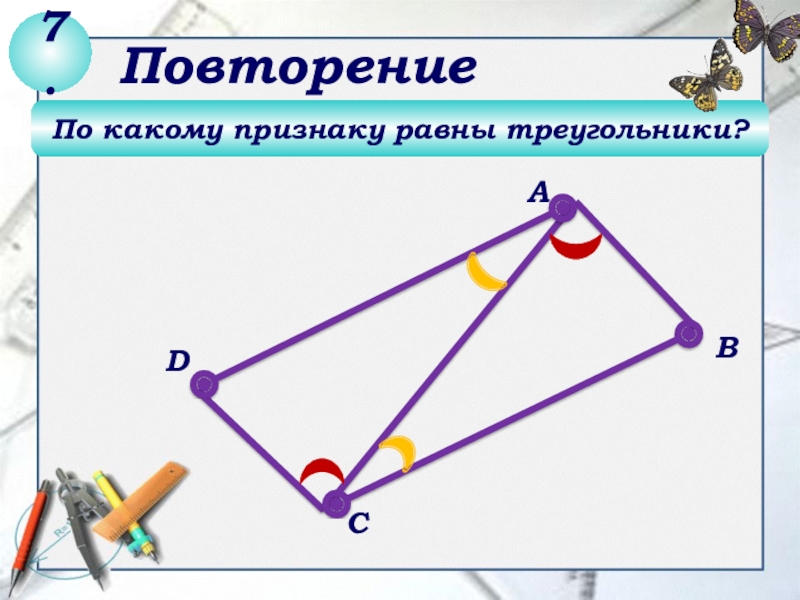
- 7. По какому признаку равны треугольники?DСВА6.Повторение
- 8. По какому признаку равны треугольники?DСВА7.Повторение
- 9. Тема урока: Параллелограмм.Урок геометрии в 8
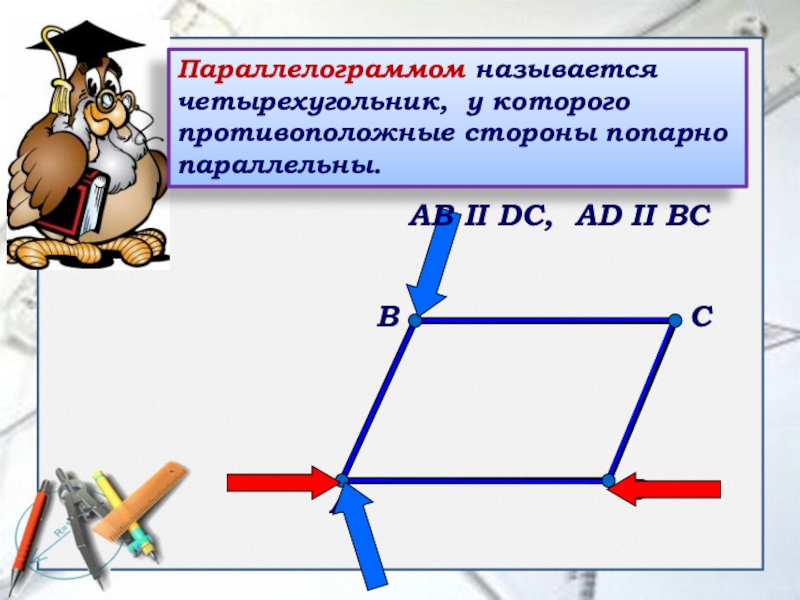
- 10. ВАСDАВ II DС, AD II BC Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
- 11. Обратите внимание:
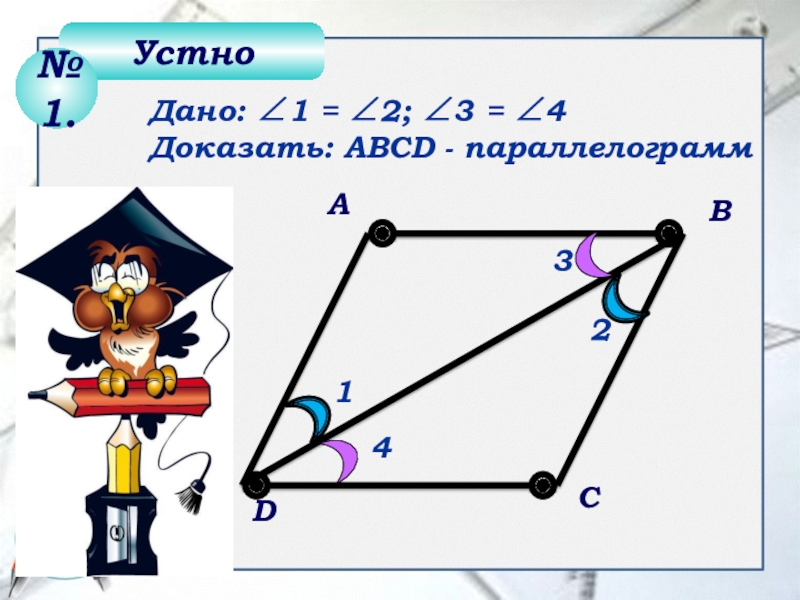
- 12. Дано: 1 = 2; 3 = 4Доказать: АВСD - параллелограмм1234DСВАУстно№1.
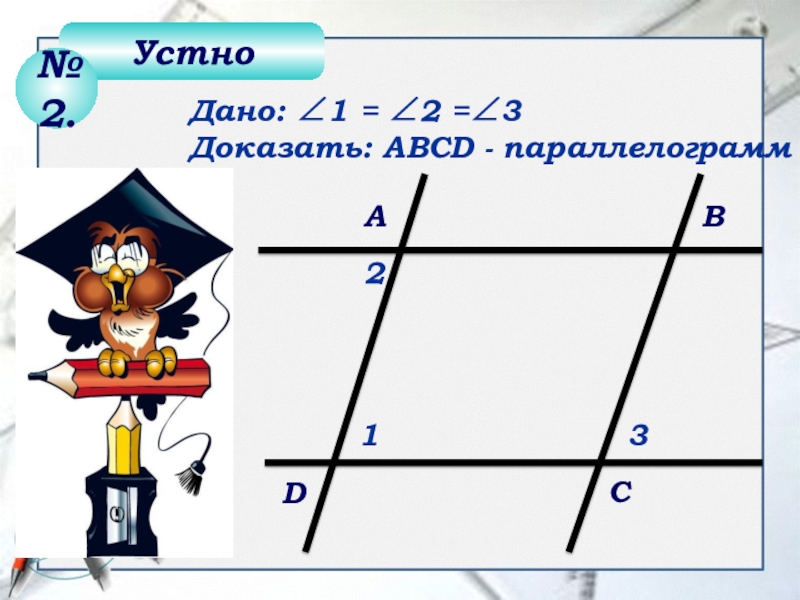
- 13. Дано: 1 = 2 =3 Доказать: АВСD - параллелограмм123DСВАУстно№2.
- 14. Дано: АВСD – четырехугольник
- 15. Решаем:№ 4№ 14стр. 79
- 16. Стороны АВ и ВС треугольника АВС продолжены
- 17. Домашнее задание.П. 51 (стр. 68)Контр. вопросы: 1
- 18. ЧетырёхугольникНайдите углы выпуклого четырёхугольника, если они равны
По какому признаку равны треугольники? DСВАО1.Повторение
Слайд 9Тема урока:
Параллелограмм.
Урок геометрии
в 8 классе.
Учитель математики МБОУ СОШ № 25
г. Крымска Малая Е.В.
Слайд 10В
А
С
D
АВ II DС, AD II BC
Параллелограммом называется четырехугольник, у которого
противоположные стороны попарно параллельны.
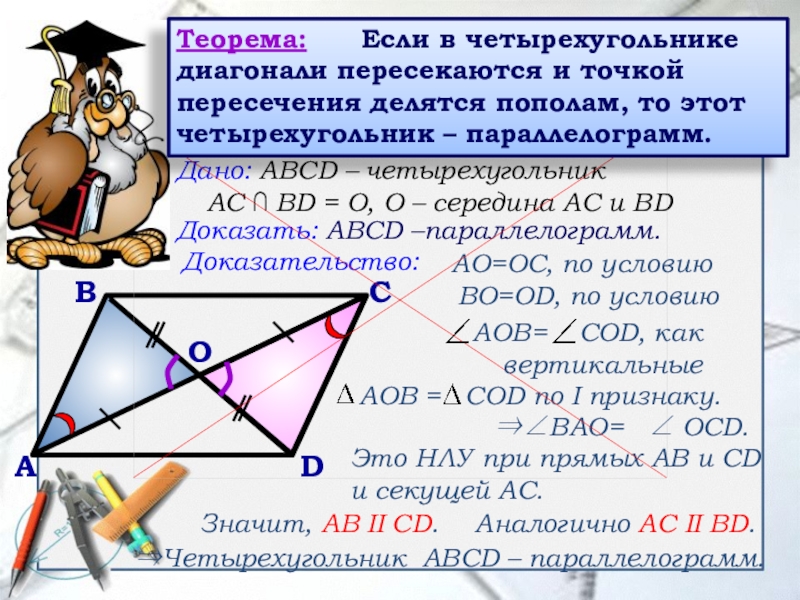
Слайд 14Дано: АВСD – четырехугольник
АС ВD = О, О – середина АС и ВD
В
А
С
D
Доказательство:
АО=ОС, по условию
ВАО= ОСD. Это НЛУ при прямых АВ и СD и секущей АС.
Значит, АВ II СD.
Четырехугольник АВСD – параллелограмм.
Доказать: АВСD –параллелограмм.
ВО=ОD, по условию
О
Теорема: Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Аналогично АС II ВD.
Слайд 16Стороны АВ и ВС треугольника АВС продолжены за точку В. ВD
= ВС; ВЕ = АВ. Докажите, что АDЕС - параллелограмм
Задача №1:
Слайд 17Домашнее задание.
П. 51 (стр. 68)
Контр. вопросы: 1 – 7 (стр. 78)
Решать:
№
3 ( стр. 79)
№ 9 (стр. 80)
№ 9 (стр. 80)
Слайд 18Четырёхугольник
Найдите углы выпуклого четырёхугольника, если они равны друг другу.
Найдите углы выпуклого
четырёхугольника, если они пропорциональны числам 1,2,4,5.
Найдите стороны четырёхугольника, если его периметр равен 8 см, а одна сторона больше каждой из других сторон соответственно на 3 мм, 4мм и 5мм.
Найдите стороны четырёхугольника, если его периметр равен 66 см, первая сторона больше второй на 8 см и на столько же меньше третьей стороны, а четвёртая в три раза больше второй.
Докажите, что если не все углы выпуклого четырёхугольника равны друг другу, то хотя бы один из них тупой.
Найдите стороны четырёхугольника, если его периметр равен 8 см, а одна сторона больше каждой из других сторон соответственно на 3 мм, 4мм и 5мм.
Найдите стороны четырёхугольника, если его периметр равен 66 см, первая сторона больше второй на 8 см и на столько же меньше третьей стороны, а четвёртая в три раза больше второй.
Докажите, что если не все углы выпуклого четырёхугольника равны друг другу, то хотя бы один из них тупой.
