- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Параллелограмм Вариньона 8 класс
Содержание
- 1. Презентация по геометрии на тему Параллелограмм Вариньона 8 класс
- 2. Пьер Вариньон (1654-1772 гг.) – французский математик
- 3. Основные работы относятся к геометрии и статике.
- 4. Пьер ВариньонЕго трактат “Новая механика, или статика”,
- 5. Теорема Вариньона: Фигура, образованная путем
- 6. Дано:произвольный выпуклыйчетырёхугольник АBCD,DL=AL,AM=BM, BN=CN, DK=CK,AC – диагональ;Доказать:теорему ВариньонаLMNK - параллелограммПодсказка:примените свойство средней линии треугольника.Теорема Вариньона:
- 7. Доказательство: Рассмотрим ∆ACD: LK – средняялиния по
- 8. Применение теоремы Вариньона к доказательству некоторых утвержденийУтверждение
- 9. Утверждение 2. Если отрезки соединяющие середины противоположных
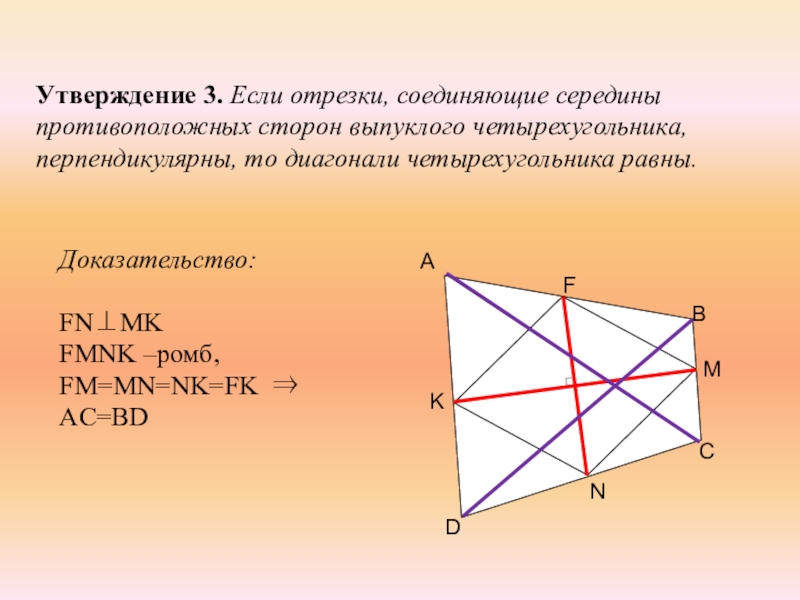
- 10. Утверждение 3. Если отрезки, соединяющие середины противоположных
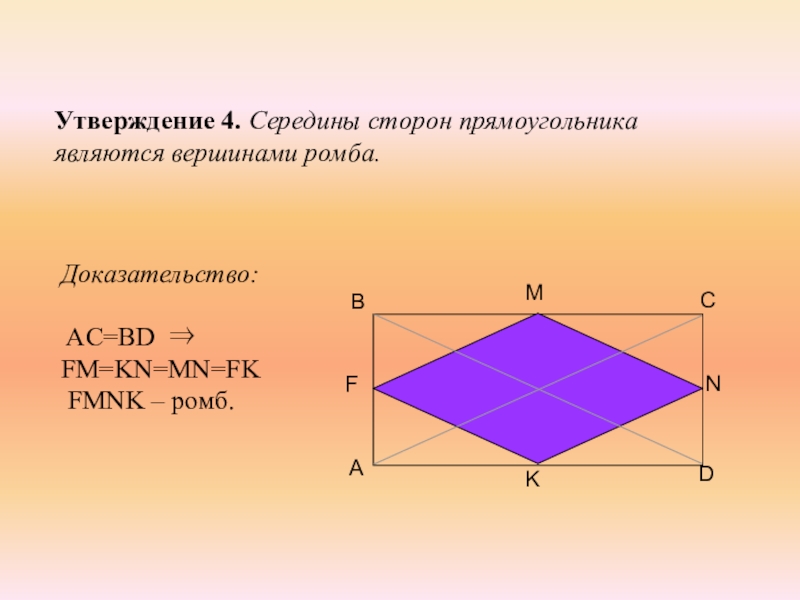
- 11. Утверждение 4. Середины сторон прямоугольника являются вершинами ромба.Доказательство: AC=BD ⇒ FM=KN=MN=FK FMNK – ромб.
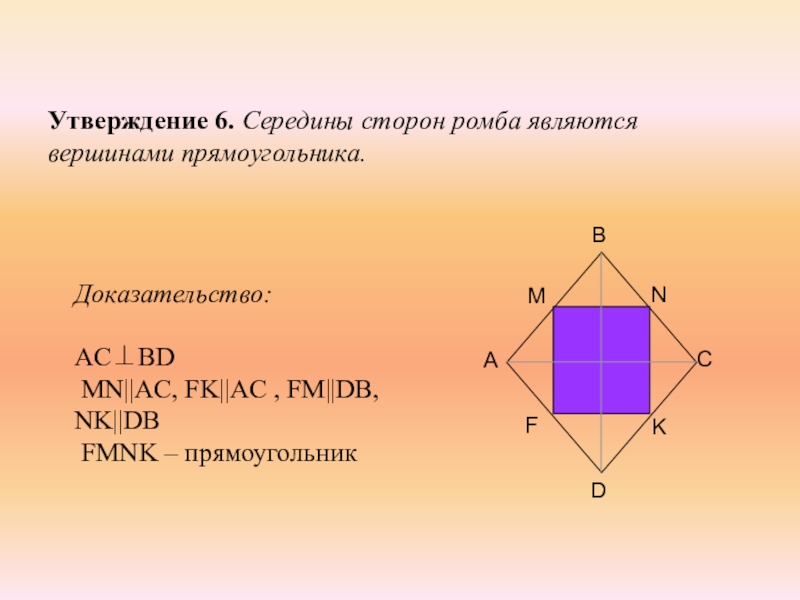
- 12. Утверждение 6. Середины сторон ромба являются вершинами
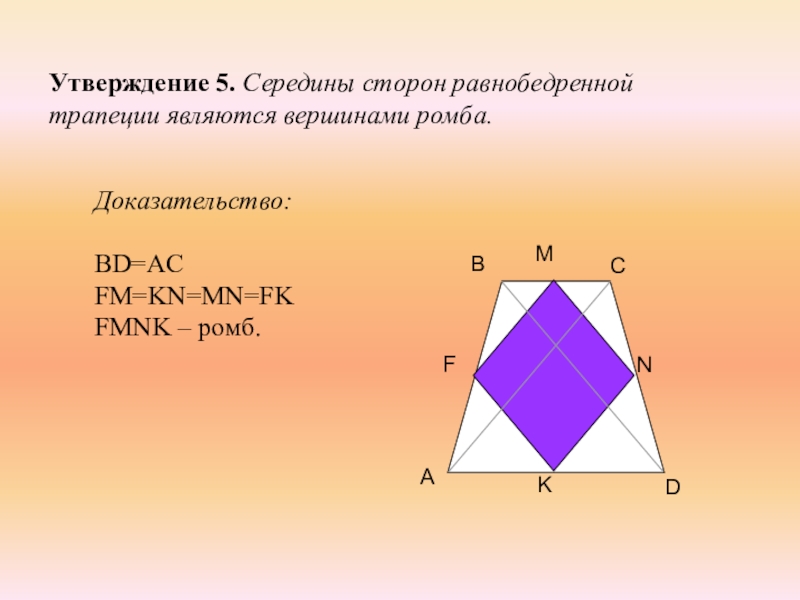
- 13. Утверждение 5. Середины сторон равнобедренной трапеции являются вершинами ромба.Доказательство: BD=AC FM=KN=MN=FK FMNK – ромб.
- 14. Результаты:Изучая теорему Пьера Вариньона я:узнал его биографию;познакомился
Слайд 1Презентация по теме «Параллелограмм Вариньона»
Работа ученика 8 класса
Щербинина Максима
Руководитель:
Слайд 2Пьер Вариньон (1654-1772 гг.) – французский математик и механик, член Французской
Родился в Каенне.
Изучал философию и математику.
С 1688 – профессор математики в Коллеже Мазарини, с 1704 – в Коллеж де Франс.
Слайд 3Основные работы относятся к геометрии и статике. Исходя из теории сложных
Развил понятие момента сил и предложил геометрическое доказательство теоремы о том, что момент равнодействующей двух сходящихся сил равен сумме моментов составляющих сил (теорема Вариньона).
Пьер Вариньон
Слайд 4Пьер Вариньон
Его трактат “Новая механика, или статика”, проект которого был опубликован
Установил (1687) теорему о скользящих векторах для случая сходящейся системы сил.
Одним из первых начал пользоваться математическим анализом.
Изучал равновесие и движение жидкости.
Дал объяснение закона Торричелли, полагая, что вес колонны воды пропорционален высоте h, нашел выражение для закона Торричелли.
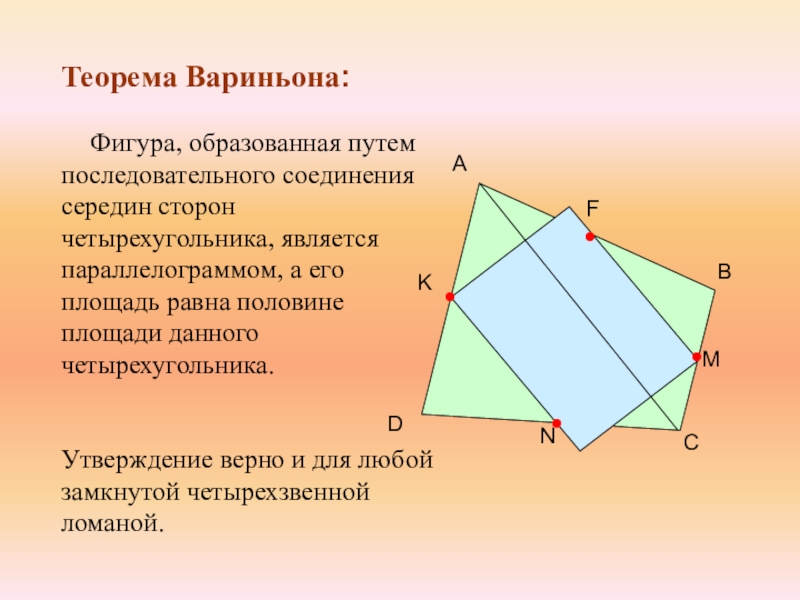
Слайд 5Теорема Вариньона:
Фигура, образованная путем последовательного соединения середин сторон
Утверждение верно и для любой замкнутой четырехзвенной ломаной.
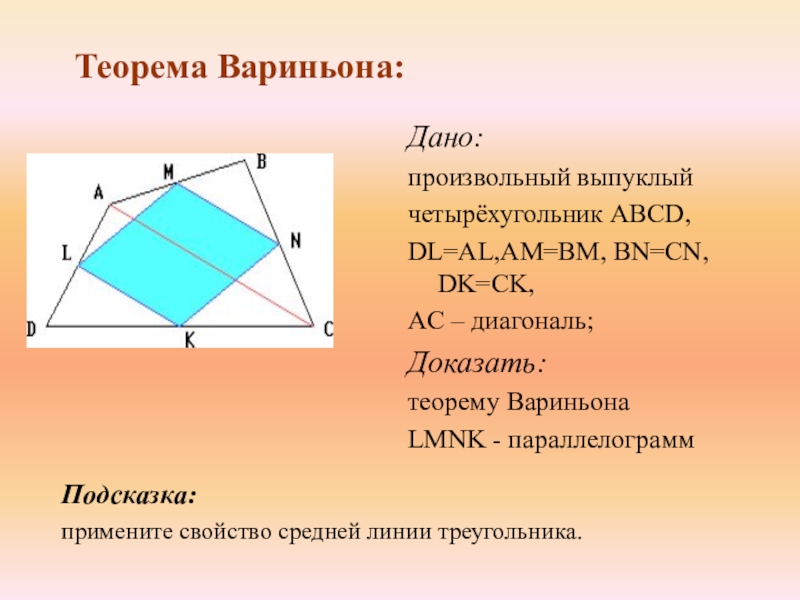
Слайд 6Дано:
произвольный выпуклый
четырёхугольник АBCD,
DL=AL,AM=BM, BN=CN, DK=CK,
AC – диагональ;
Доказать:
теорему Вариньона
LMNK - параллелограмм
Подсказка:
примените свойство
Теорема Вариньона:
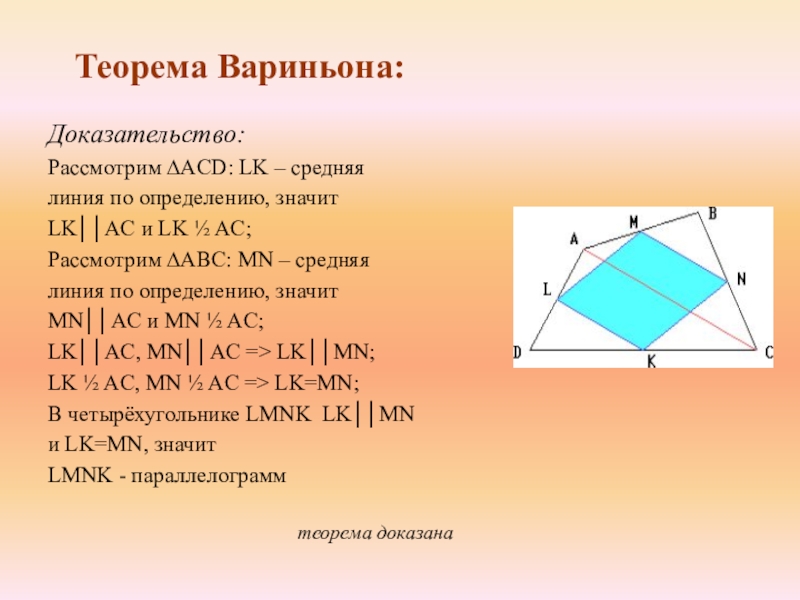
Слайд 7Доказательство:
Рассмотрим ∆ACD: LK – средняя
линия по определению, значит
LK││AC и LK
Рассмотрим ∆ABC: MN – средняя
линия по определению, значит
MN││AC и MN ½ AC;
LK││AC, MN││AC => LK││MN;
LK ½ AC, MN ½ AC => LK=MN;
В четырёхугольнике LMNK LK││MN
и LK=MN, значит
LMNK - параллелограмм
теорема доказана
Теорема Вариньона:
Слайд 8Применение теоремы Вариньона к доказательству некоторых утверждений
Утверждение 1. В выпуклом четырехугольнике
Доказательство:
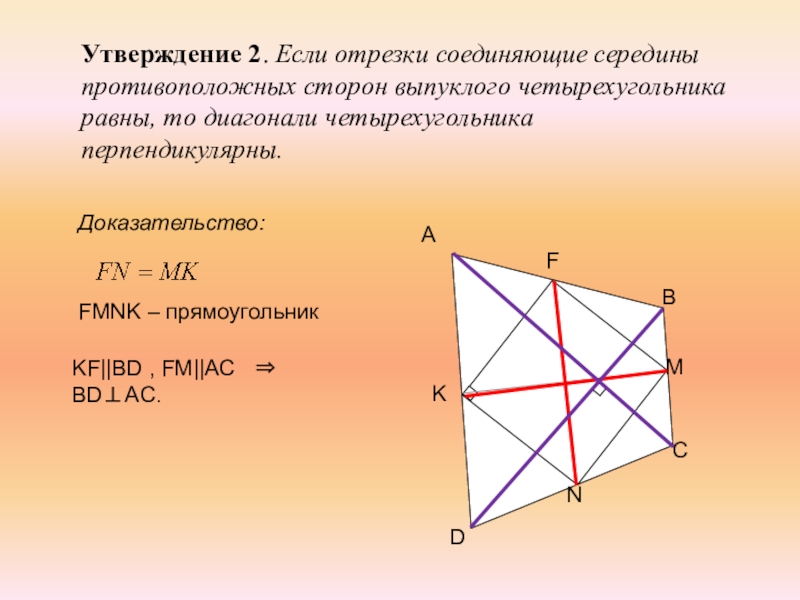
Слайд 9Утверждение 2. Если отрезки соединяющие середины противоположных сторон выпуклого четырехугольника равны,
Доказательство:
FMNK – прямоугольник
KF||BD , FM||AC ⇒ BD⊥AC.
Слайд 10
Утверждение 3. Если отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника, перпендикулярны,
Доказательство:
FN⊥MK
FMNK –ромб,
FM=MN=NK=FK ⇒ AC=BD
Слайд 11Утверждение 4. Середины сторон прямоугольника являются вершинами ромба.
Доказательство:
AC=BD ⇒ FM=KN=MN=FK
Слайд 12Утверждение 6. Середины сторон ромба являются вершинами прямоугольника.
Доказательство:
AC⊥BD
MN||AC,
FMNK – прямоугольник
Слайд 13Утверждение 5. Середины сторон равнобедренной трапеции являются вершинами ромба.
Доказательство:
BD=AC
FM=KN=MN=FK
FMNK – ромб.
Слайд 14Результаты:
Изучая теорему Пьера Вариньона я:
узнал его биографию;
познакомился с параллелограммом Вариньона;
доказал теорему;
Рассмотрел