:
«Параллелограмм и его свойства»
учителя математики
ГБОУ школы №1056
Романенко Елены Алексеевны
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Параллелограмм и его свойства
Содержание
- 1. Презентация по геометрии на тему Параллелограмм и его свойства
- 2. Параллелограмм
- 3. Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны.AB || CDBC || ADDCAB
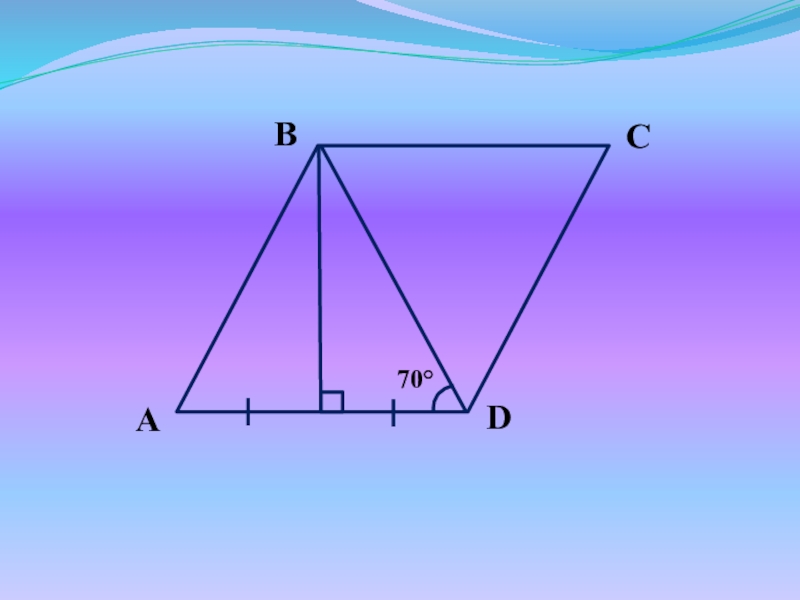
- 4. Задачи для устного решенияДокажите, что ABCD – параллелограмм.
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Свойства параллелограммаСумма углов, прилежащих к одной стороне,
- 11. Слайд 11
- 12. Сумма углов, прилежащих к одной стороне, равна 180˚.Дано:ABCD – пар-мДоказать:A + B = 180˚DCAB
- 13. Доказательство:ABCD – пар-м, зн. BC||AD (по определению)2)
- 14. Противолежащие углы равны.Дано:ABCD – пар-мДоказать:A = CB = D DCAB
- 15. Доказательство:ABCD – пар-м,значит AB||CD, BC||AD (по определению)A
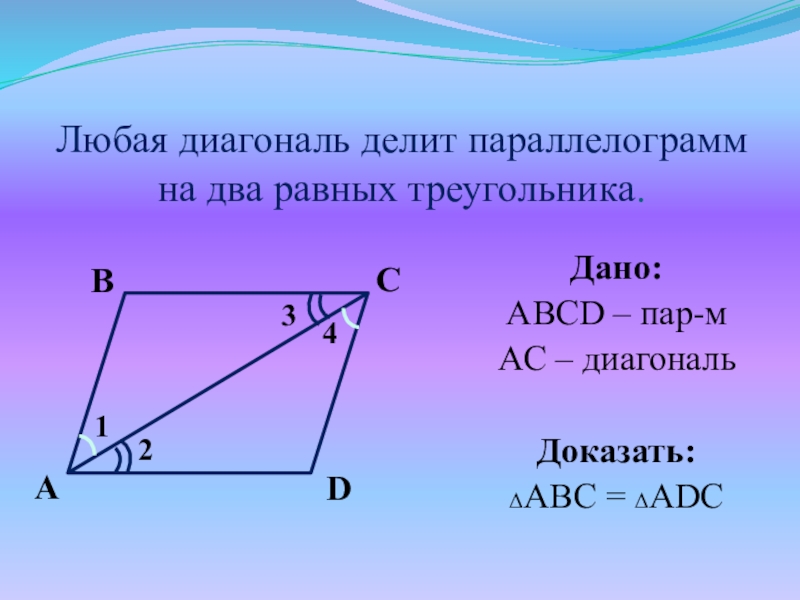
- 16. Любая диагональ делит параллелограмм на два равных треугольника. Дано:ABCD – пар-мAC – диагональДоказать:ΔABC = ΔADCDCAB4213
- 17. Доказательство:ABCD – пар-м,значит AB||CD, BC||AD (по определению)1
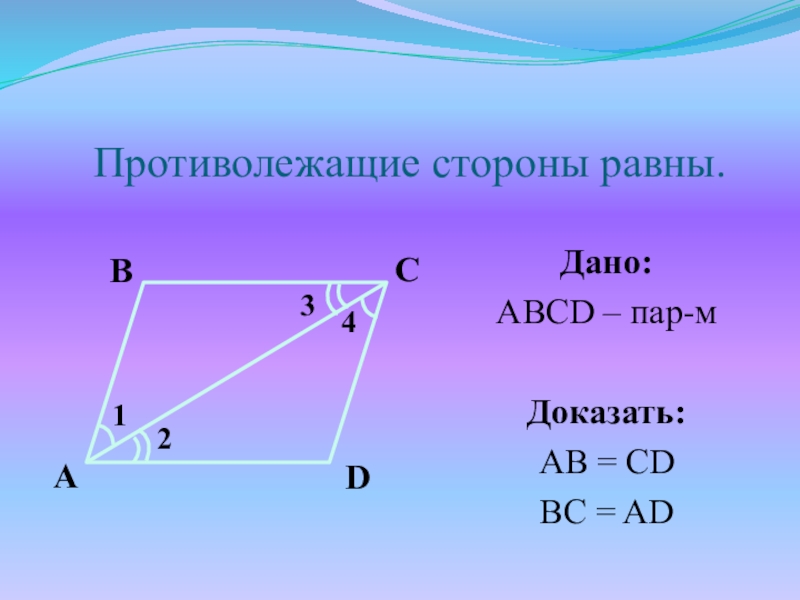
- 18. Противолежащие стороны равны.Дано:ABCD – пар-мДоказать:AB = CDBC = AD DCAB4213
- 19. Доказательство:ABCD – пар-м, AC – диагональAB||CD, BC||AD
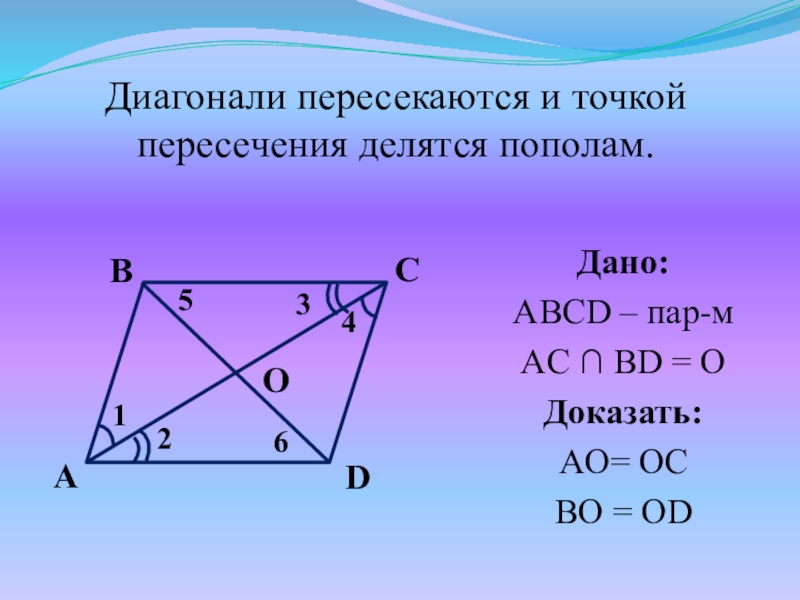
- 20. DCAB4213Дано:ABCD – пар-мAC ∩ BD = OДоказать:AO=
- 21. Доказательство:ABCD – пар-м, зн. AB||CD, BC||AD 1
- 22. Задачи для устного решения
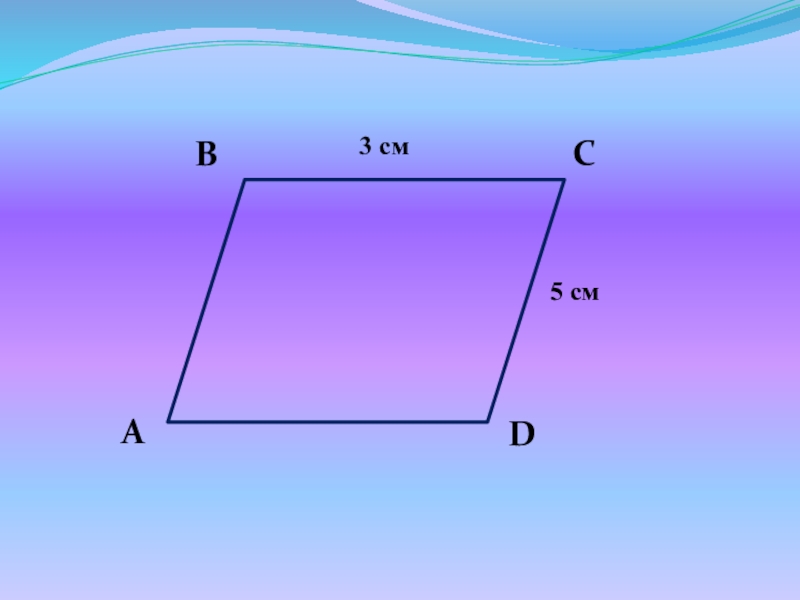
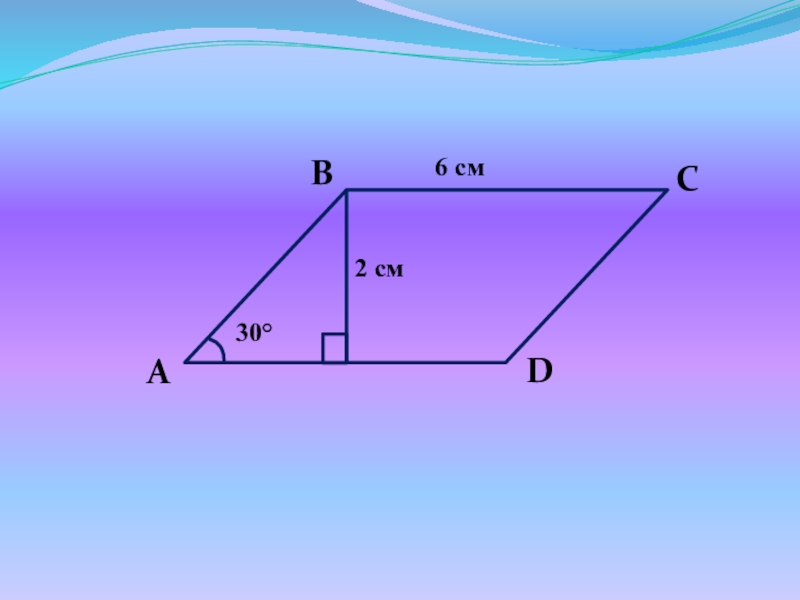
- 23. Найдите периметр параллелограмма.
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
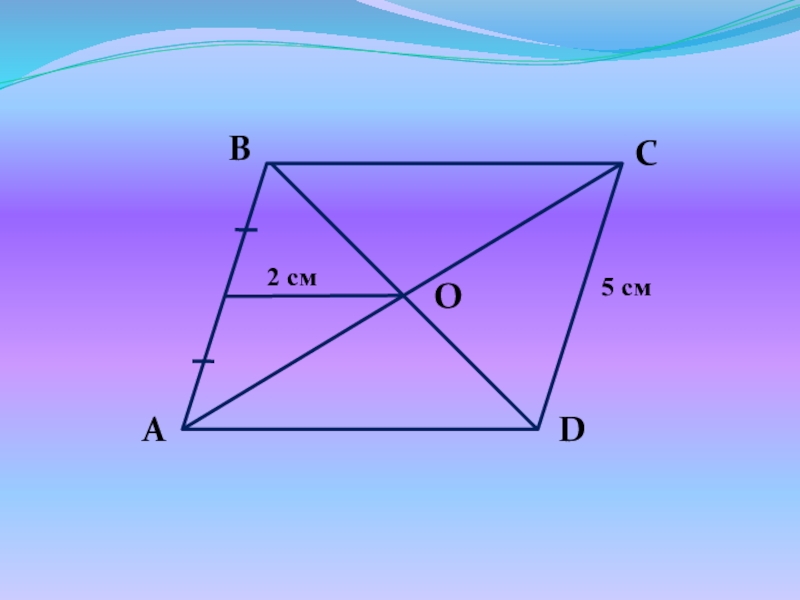
- 27. Найдите все неизвестные углы параллелограмма.
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
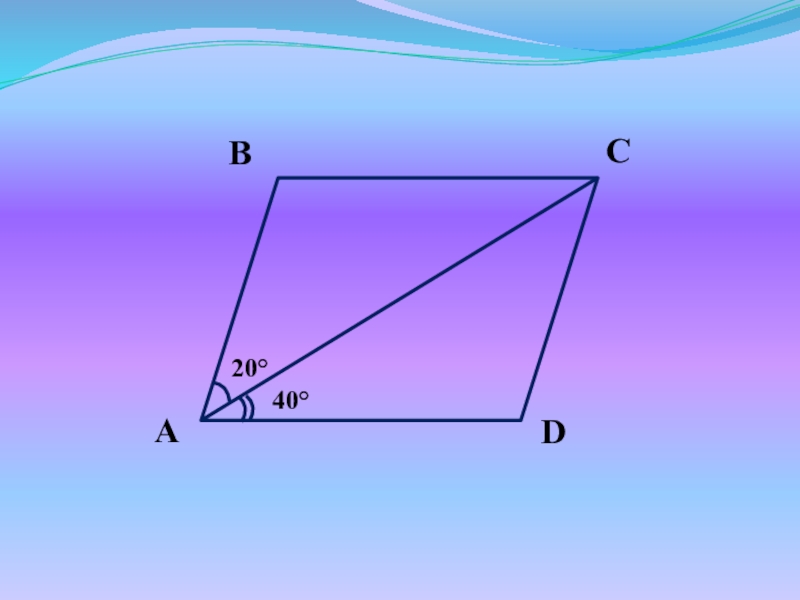
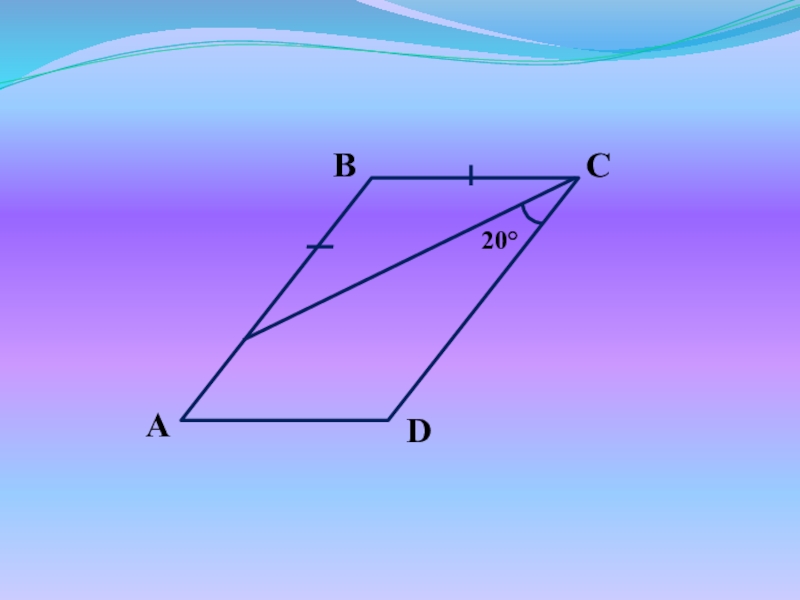
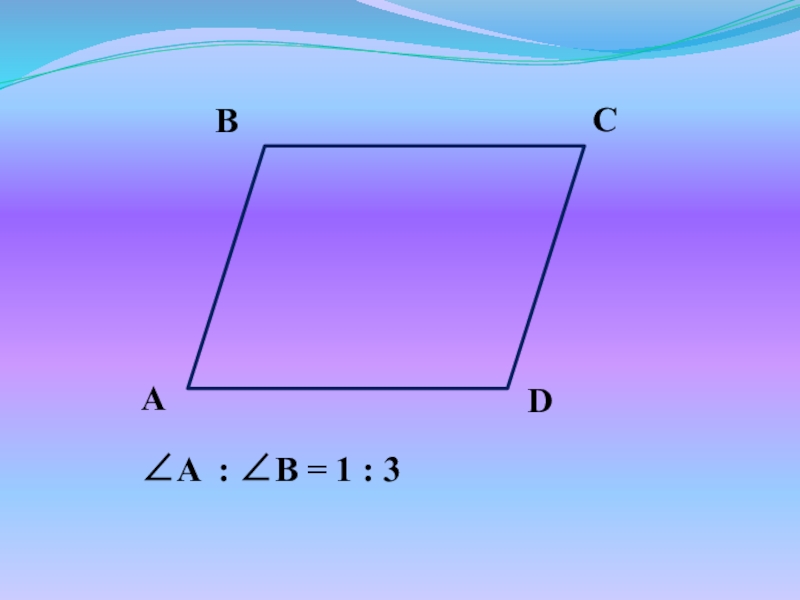
- 31. Найдите углы параллелограмма ABCD.
- 32. B – A = 30
- 33. A : B = 1 : 3
Параллелограмм
Слайд 1Департамент образования города Москвы
Северо-Западное окружное управление образования
Презентация по геометрии на тему
Слайд 3Параллелограмм -
это четырехугольник, у которого противоположные стороны попарно параллельны.
AB ||
CD
BC || AD
BC || AD
D
C
A
B
Слайд 10Свойства параллелограмма
Сумма углов, прилежащих к одной стороне, равна 180˚.
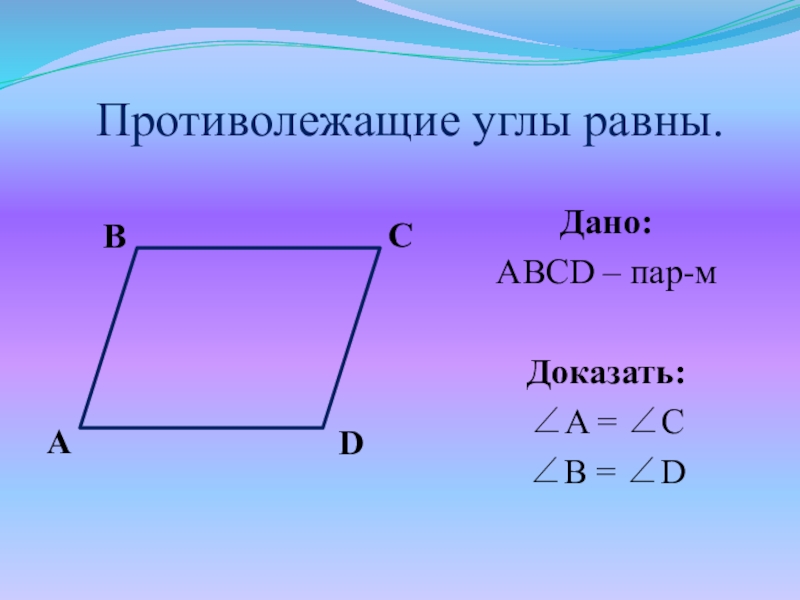
Противолежащие углы
равны.
Любая диагональ делит параллелограмм на два равных треугольника.
Противолежащие стороны равны.
Диагонали пересекаются и точкой пересечения делятся пополам.
Любая диагональ делит параллелограмм на два равных треугольника.
Противолежащие стороны равны.
Диагонали пересекаются и точкой пересечения делятся пополам.
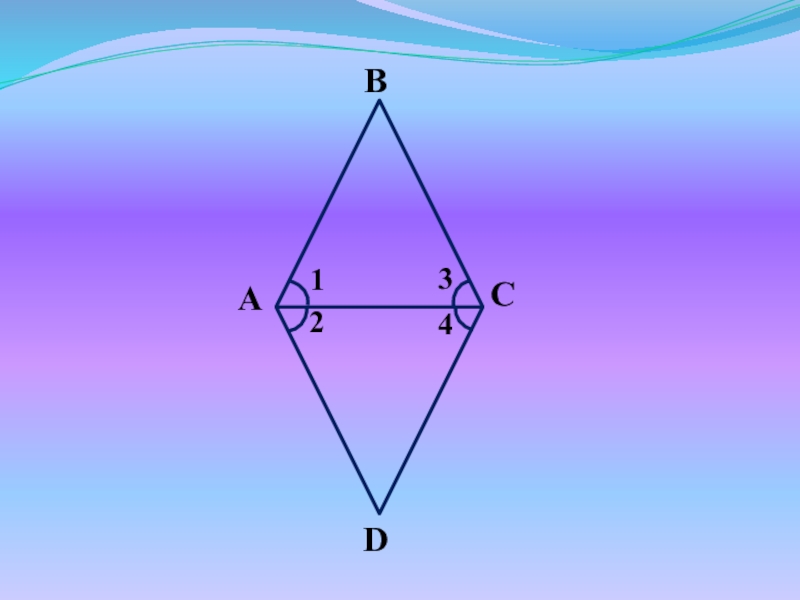
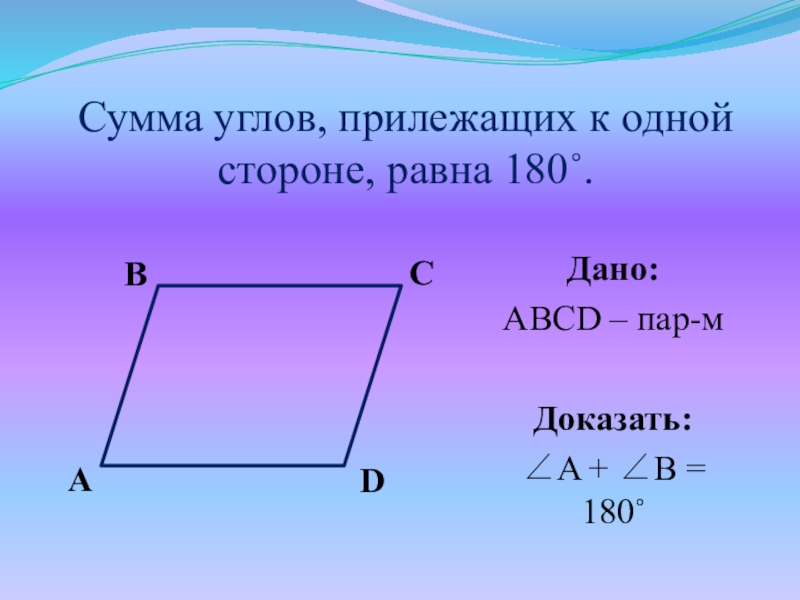
Слайд 12Сумма углов, прилежащих к одной стороне, равна 180˚.
Дано:
ABCD – пар-м
Доказать:
A +
B = 180˚
D
C
A
B
Слайд 13Доказательство:
ABCD – пар-м,
зн. BC||AD (по определению)
2) Рассмотрим BC||AD и секущую
AB:
A и B – внутренние односторонние при параллельных прямых, зн. A + B = 180
3) Аналогично доказываем:
B + C = C + D = A + D = 180
ч.т.д.
A и B – внутренние односторонние при параллельных прямых, зн. A + B = 180
3) Аналогично доказываем:
B + C = C + D = A + D = 180
ч.т.д.
Слайд 15Доказательство:
ABCD – пар-м,
значит AB||CD, BC||AD (по определению)
A + B = 180,
A = 180 - B,
B + C = 180, C = 180 - B,
Следовательно, A = С.
2) ABCD – пар-м,
значит AB||CD, BC||AD (по определению)
D + C = 180, D = 180 - C,
B + C = 180, B = 180 - C,
Следовательно, B = D.
ч.т.д.
B + C = 180, C = 180 - B,
Следовательно, A = С.
2) ABCD – пар-м,
значит AB||CD, BC||AD (по определению)
D + C = 180, D = 180 - C,
B + C = 180, B = 180 - C,
Следовательно, B = D.
ч.т.д.
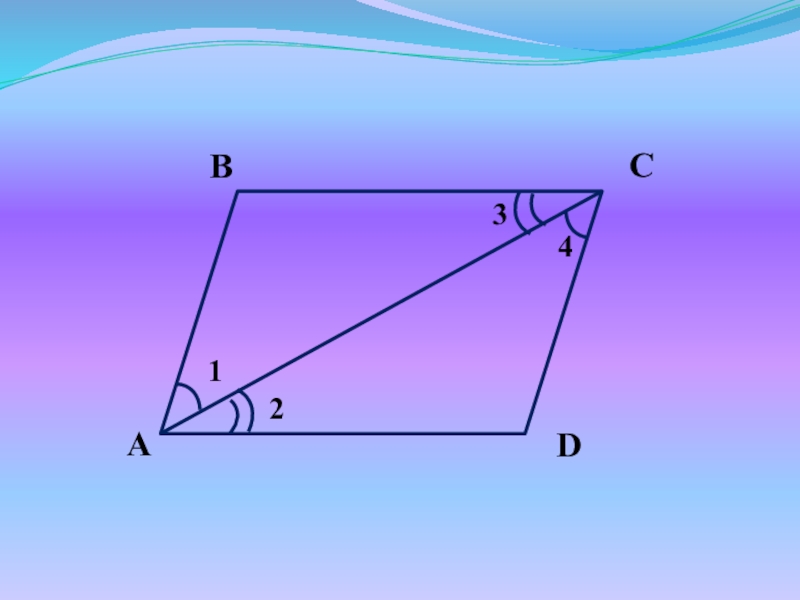
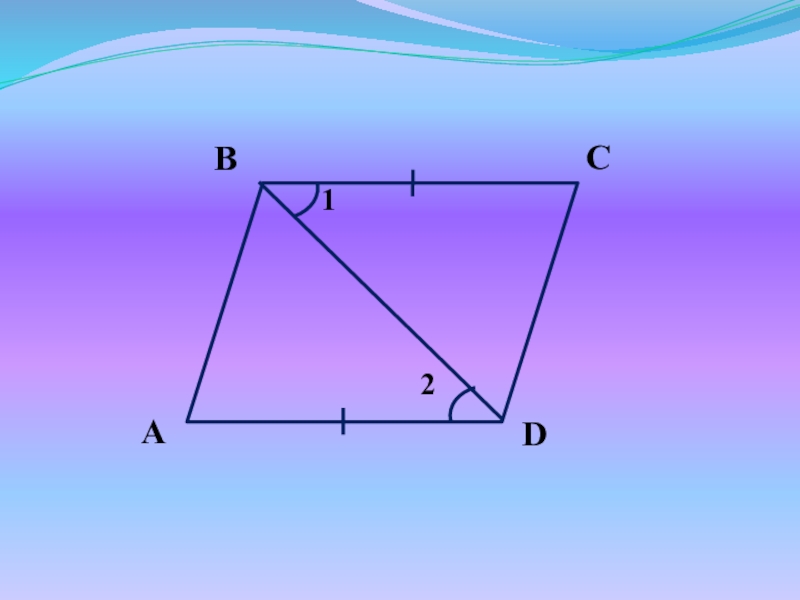
Слайд 16Любая диагональ делит параллелограмм на два равных треугольника.
Дано:
ABCD – пар-м
AC
– диагональ
Доказать:
ΔABC = ΔADC
Доказать:
ΔABC = ΔADC
D
C
A
B
4
2
1
3
Слайд 17Доказательство:
ABCD – пар-м,
значит AB||CD, BC||AD (по определению)
1 = 4 , 2
= 3 (как внутренние накрест лежащие)
Рассмотрим ΔABC и ΔADC:
1 = 4
2 = 3
AC – общая
Следовательно, ΔABC = ΔADC (по II признаку)
ч.т.д.
Рассмотрим ΔABC и ΔADC:
1 = 4
2 = 3
AC – общая
Следовательно, ΔABC = ΔADC (по II признаку)
ч.т.д.
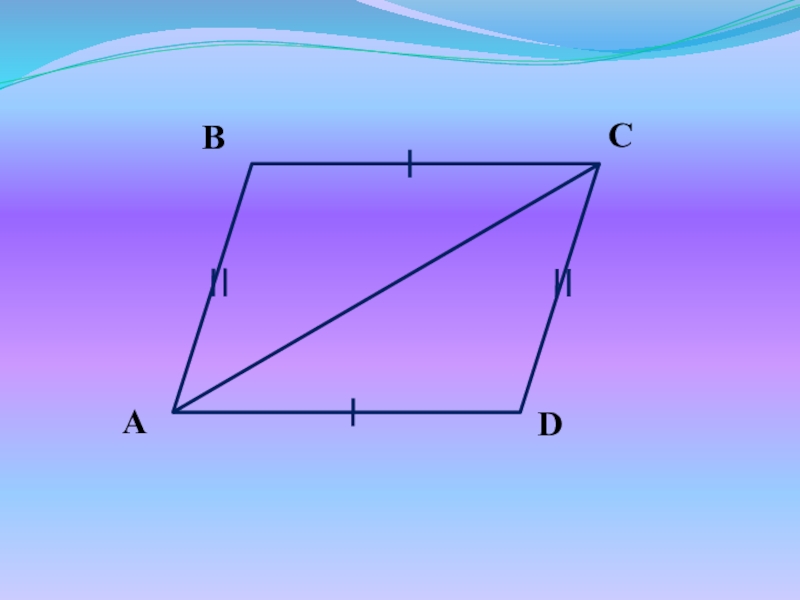
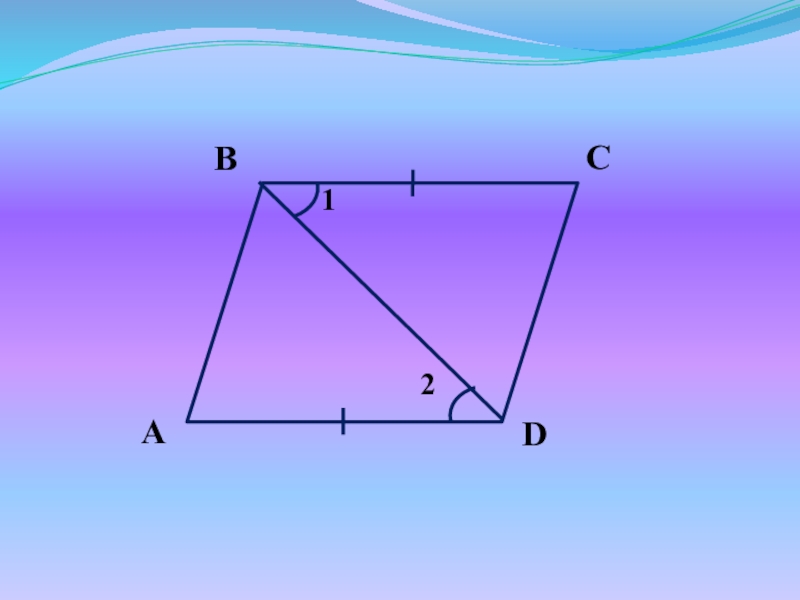
Слайд 19Доказательство:
ABCD – пар-м, AC – диагональ
AB||CD, BC||AD (по определению)
1 = 4
, 2 = 3 (как внутренние накрест лежащие)
Рассмотрим ΔABC и ΔADC:
1 = 4
2 = 3
AC – общая
Следовательно, ΔABC = ΔADC (по II признаку),
значит AB = CD, BC = AD
ч.т.д.
Рассмотрим ΔABC и ΔADC:
1 = 4
2 = 3
AC – общая
Следовательно, ΔABC = ΔADC (по II признаку),
значит AB = CD, BC = AD
ч.т.д.
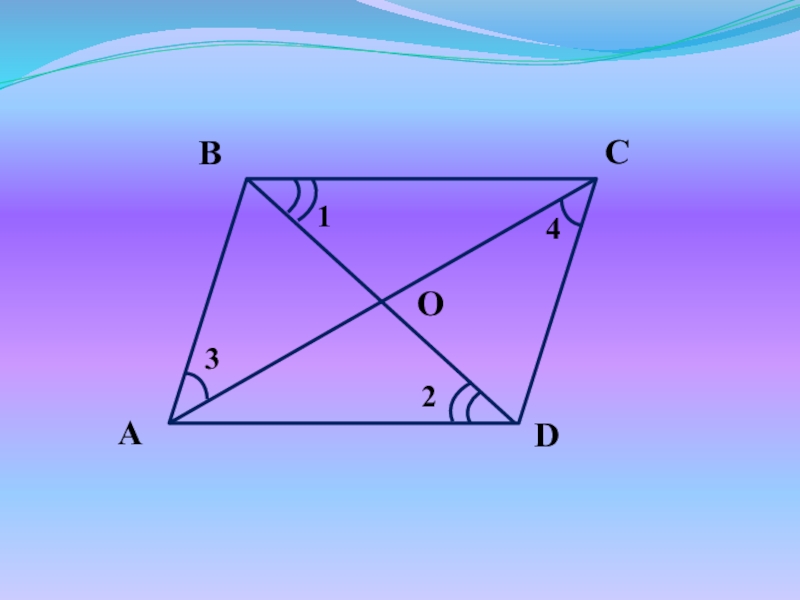
Слайд 20D
C
A
B
4
2
1
3
Дано:
ABCD – пар-м
AC ∩ BD = O
Доказать:
AO= OC
BO = OD
Диагонали
пересекаются и точкой пересечения делятся пополам.
O
5
6
Слайд 21Доказательство:
ABCD – пар-м, зн. AB||CD, BC||AD
1 = 4 , 2
= 3, 5 = 6 (как внутренние накрест лежащие)
Рассмотрим ΔABC и ΔADC:
1 = 4 ΔABC = ΔADC
2 = 3 (по II признаку)
AC – общая Значит BC = AD
3) Рассмотрим ΔAOD и ΔBOC:
5 = 6 ΔAOD = ΔBOC
2 = 3 (по II признаку)
BC = AD Значит AO = OC, BO = OD
ч.т.д.
Рассмотрим ΔABC и ΔADC:
1 = 4 ΔABC = ΔADC
2 = 3 (по II признаку)
AC – общая Значит BC = AD
3) Рассмотрим ΔAOD и ΔBOC:
5 = 6 ΔAOD = ΔBOC
2 = 3 (по II признаку)
BC = AD Значит AO = OC, BO = OD
ч.т.д.