- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Отношение площадей треугольников (8 класс)
Содержание
- 1. Презентация по геометрии на тему Отношение площадей треугольников (8 класс)
- 2. Цель урока1. Доказать теорему об отношении площадей
- 3. План урока1. Проверка выполнения домашней работы.2. Доказательство теоремы.3. Решение задач.4. Домашнее задание.
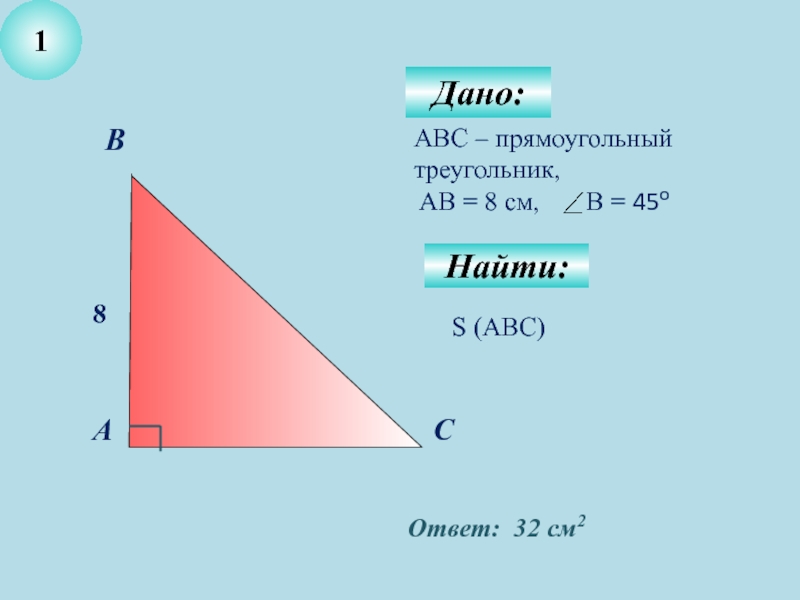
- 4. Дано:1АВС – прямоугольный треугольник, AB =
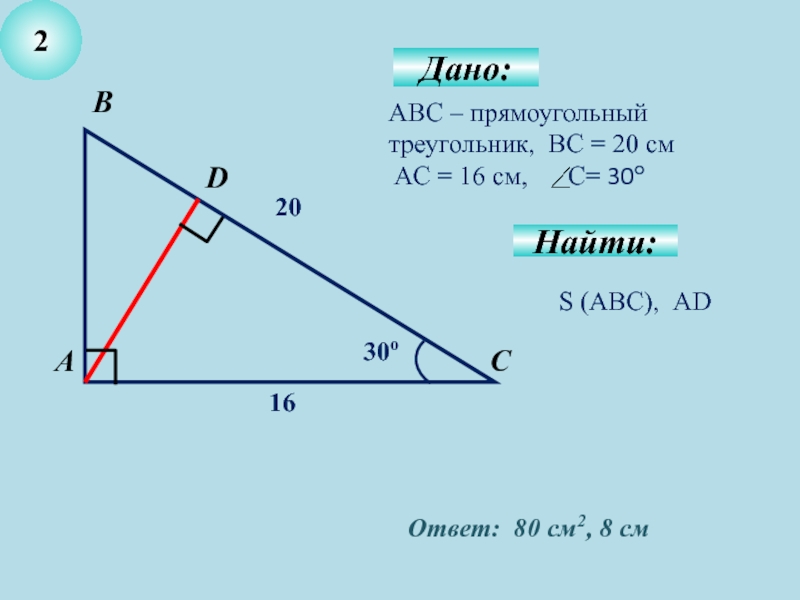
- 5. 2Дано:Найти:АВС – прямоугольный треугольник, ВС = 20
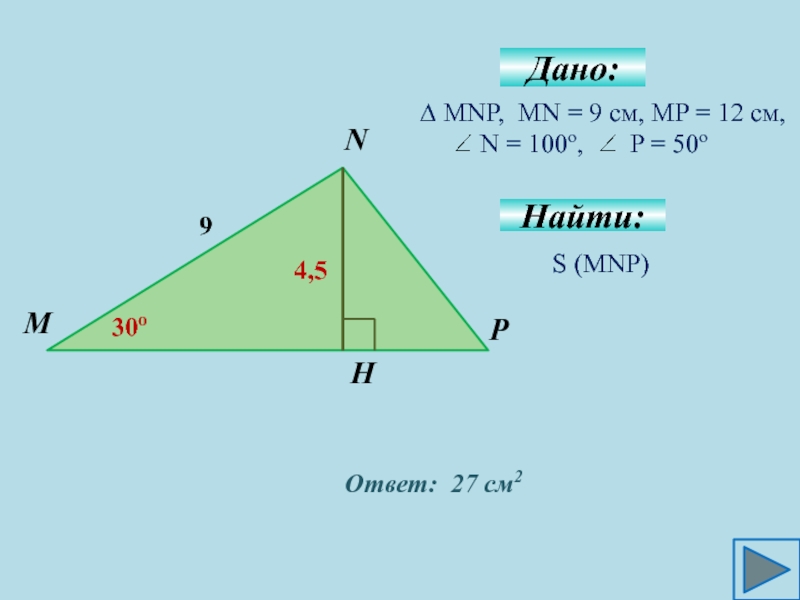
- 6. ∆ MNP, MN = 9 см, MP
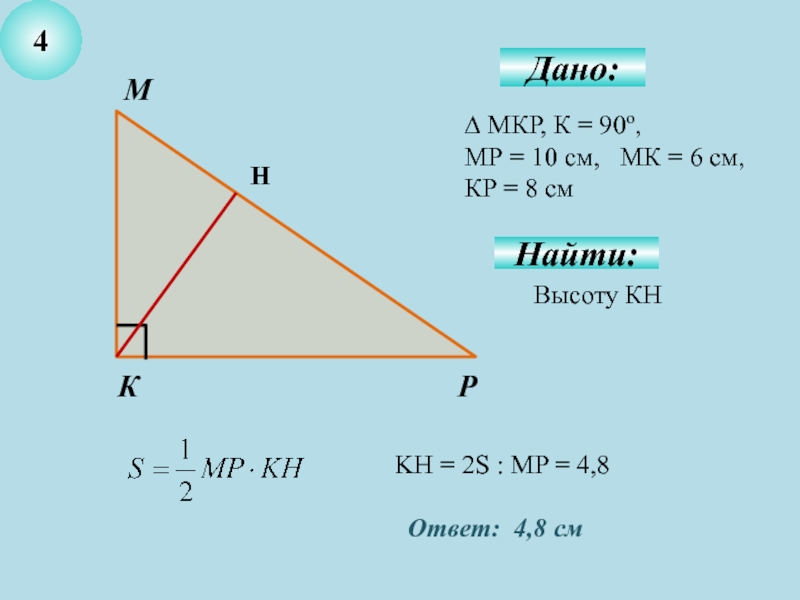
- 7. 4Дано:∆ МКР, К = 90о, МР =
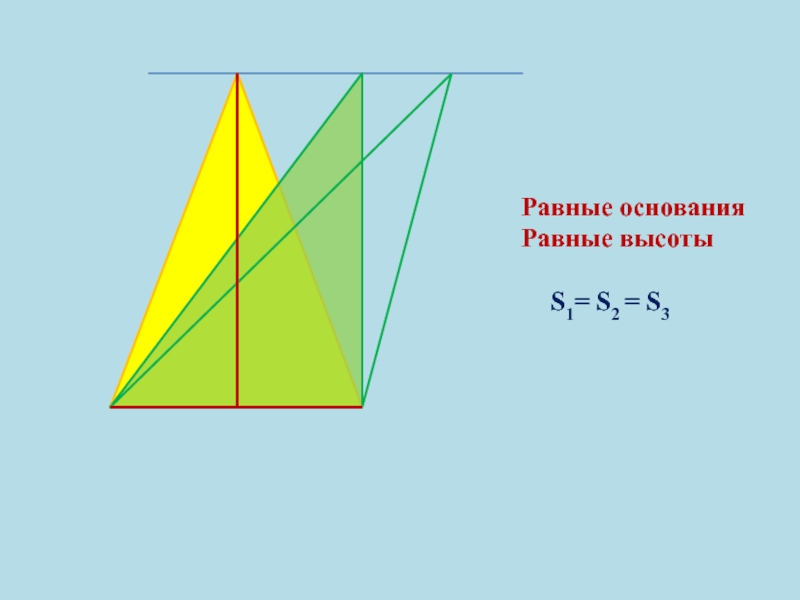
- 8. Равные основанияРавные высоты S1= S2 = S3
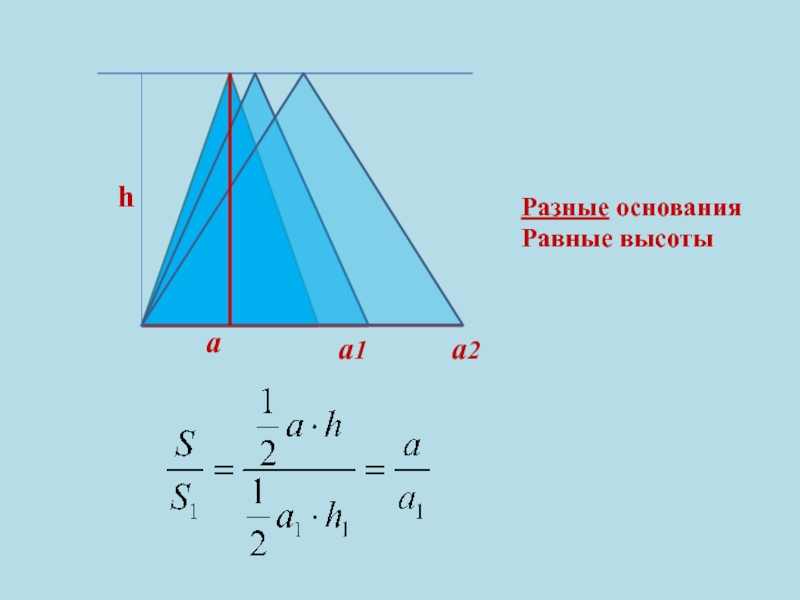
- 9. haa1a2Разные основанияРавные высоты
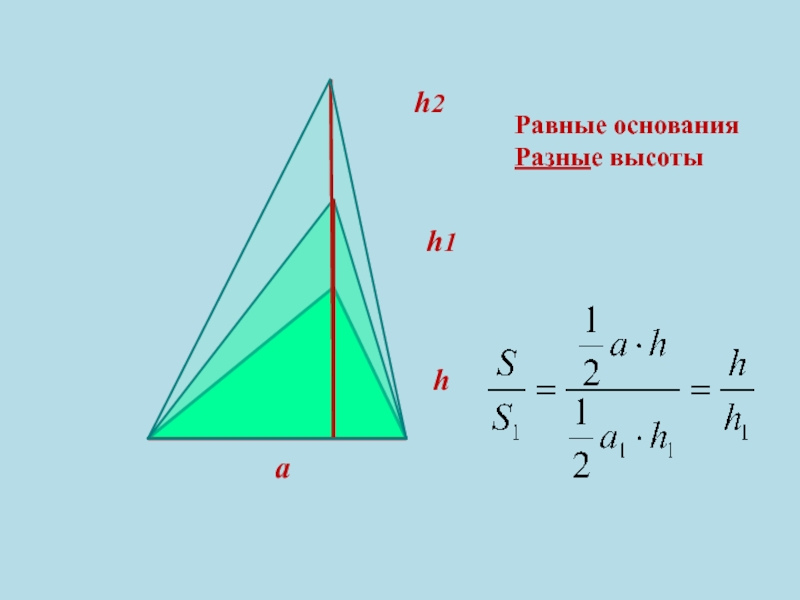
- 10. ahh1h2Равные основанияРазные высоты
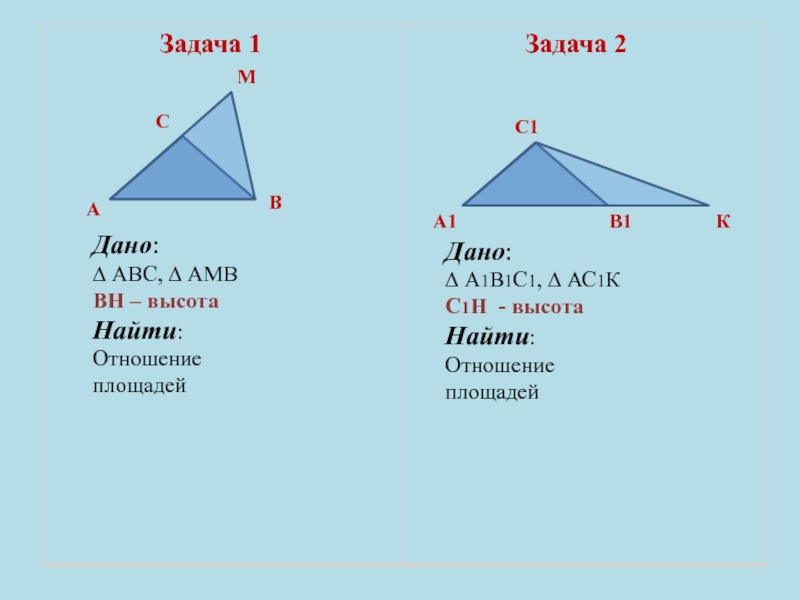
- 11. Задача 1Задача 2АСВМДано:∆ АВС, ∆ АМВВН – высотаНайти:Отношение площадейА1В1С1КДано:∆ А1В1С1, ∆ АС1КС1Н - высотаНайти:Отношение площадей
- 12. АМСВВ1А1С1КАА(А1)СКМВ
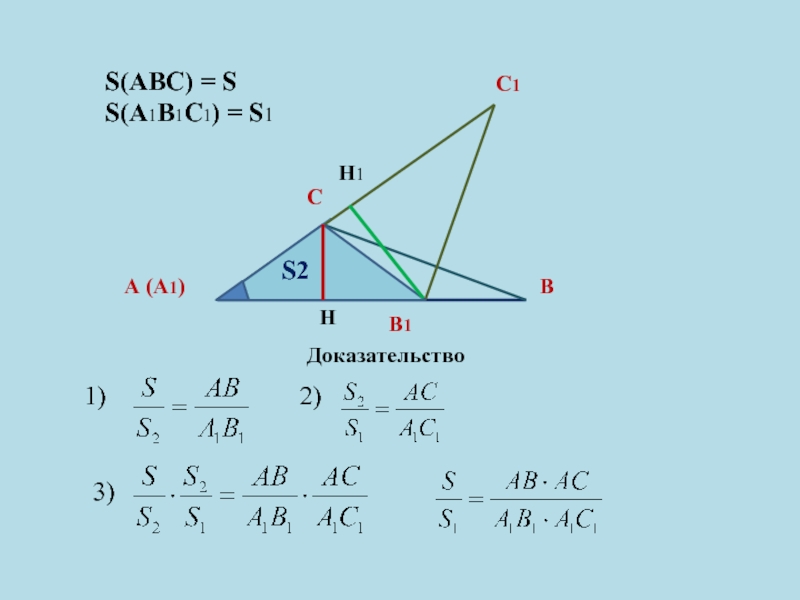
- 13. Слайд 13
- 14. Домашнее задание:п.52. Хорошо разобраться в доказательстве теоремы.Повторить
Цель урока1. Доказать теорему об отношении площадей треугольников, имеющих по равному углу.2. Рассмотреть её применение при решении задач.
Слайд 2Цель урока
1. Доказать теорему об отношении площадей треугольников, имеющих по равному
углу.
2. Рассмотреть её применение при решении задач.
2. Рассмотреть её применение при решении задач.
Слайд 3План урока
1. Проверка выполнения домашней работы.
2. Доказательство теоремы.
3. Решение задач.
4. Домашнее
задание.
Слайд 52
Дано:
Найти:
АВС – прямоугольный треугольник, ВС = 20 см
AС = 16
cм, С= 30о
А
B
C
D
S (ABC), АD
16
30о
20
Ответ: 80 см2, 8 см
Слайд 74
Дано:
∆ МКР, К = 90о,
МР = 10 см, МК
= 6 см, КР = 8 см
Найти:
M
P
К
Высоту КН
Н
KH = 2S : MP = 4,8
Ответ: 4,8 см
Слайд 11Задача 1
Задача 2
А
С
В
М
Дано:
∆ АВС, ∆ АМВ
ВН – высота
Найти:
Отношение
площадей
А1
В1
С1
К
Дано:
∆ А1В1С1, ∆
АС1К
С1Н - высота
Найти:
Отношение
площадей
С1Н - высота
Найти:
Отношение
площадей
Слайд 14Домашнее задание:
п.52. Хорошо разобраться в доказательстве теоремы.
Повторить доказательство теорем о вычислении
площади параллелограмма и площади треугольника.
№ 479 (б).
По желанию: задача
«Куда делся квадратик?»
№ 479 (б).
По желанию: задача
«Куда делся квадратик?»