СОШ № 5 имени Ю. А. Гагарина г. Тамбова
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему: Объемы фигур( 11 класс)
Содержание
- 1. Презентация по геометрии на тему: Объемы фигур( 11 класс)
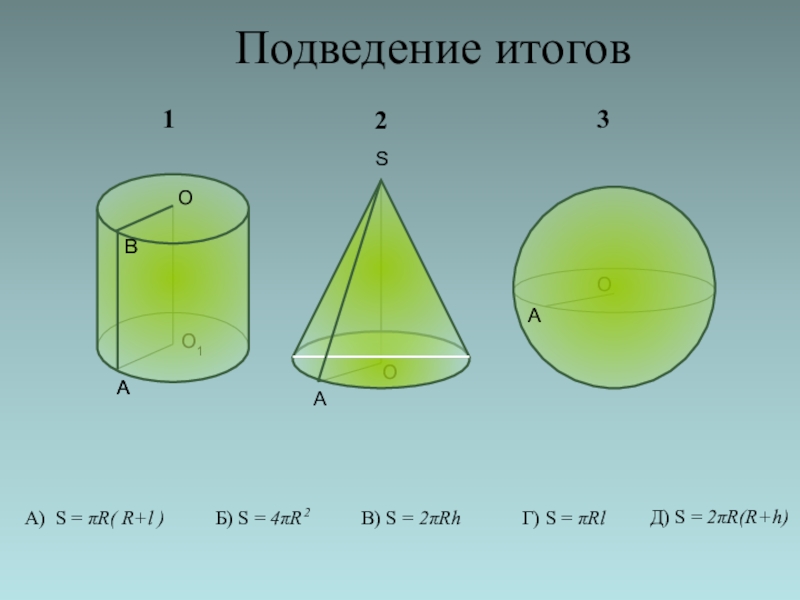
- 2. Подведение итогов В) S = 2πRhД)
- 3. Любое геометрическое тело в пространстве характеризуется величиной,
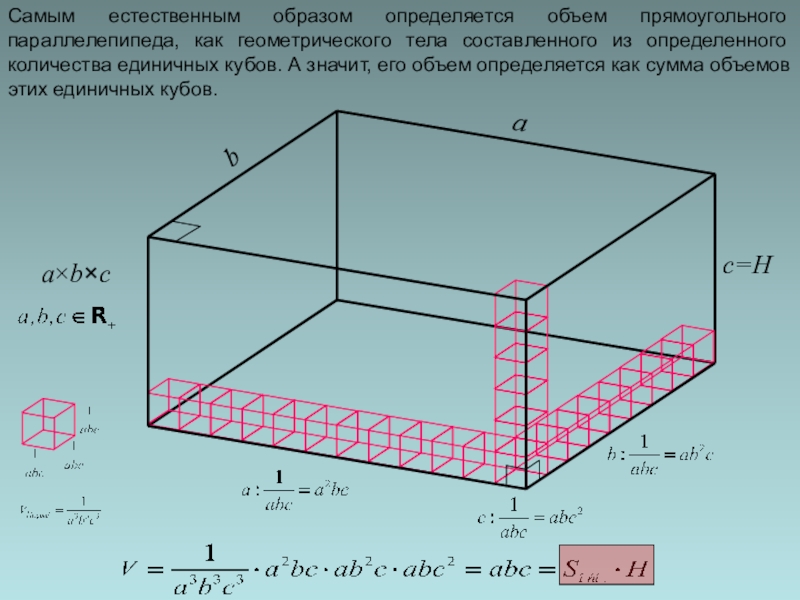
- 4. abc=Ha×b×cСамым естественным образом определяется объем прямоугольного параллелепипеда,
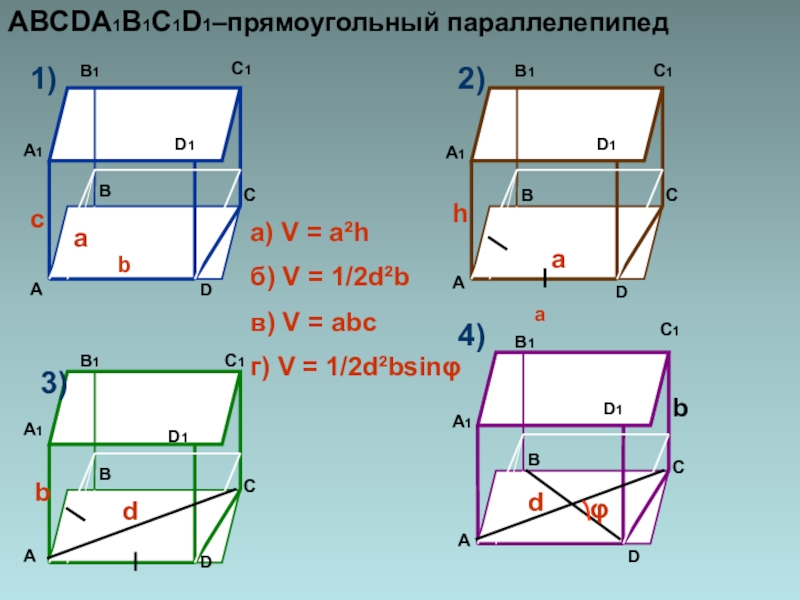
- 5. ABCDA1B1C1D1–прямоугольный параллелепипеда) V = a²hб) V = 1/2d²bв) V = abcг) V = 1/2d²bsinφВ1В1С1С1А1А1D1D1D1D1А1А1В1В1С1С1ССССААААВВВВDDDD1)2)3)4)асhdbbdφbаа
- 6. Объём прямоугольного параллелепипедаТеорема: объём прямоугольного параллелепипеда равен
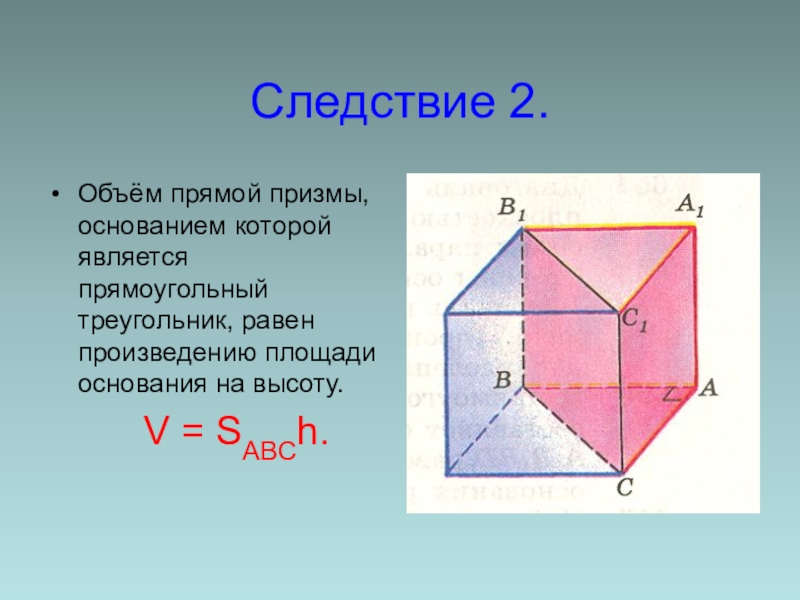
- 7. Следствие 2.Объём прямой призмы, основанием которой является
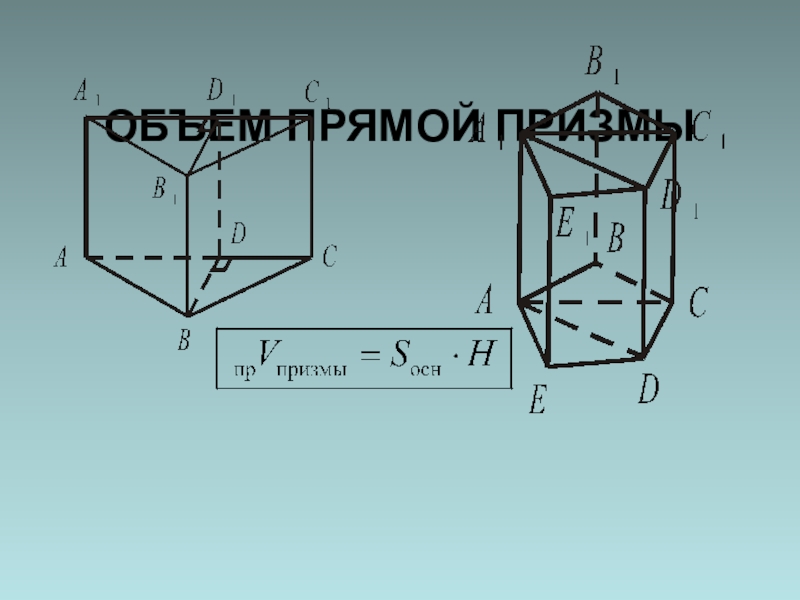
- 8. ОБЪЕМ ПРЯМОЙ ПРИЗМЫ
- 9. Итак, для любой n-угольной призмы:ИЛИ,где Sосн. –
- 10. Объём цилиндра Объём цилиндра равен произведению площади основания на высоту.
- 11. V=V1+V2+V3==S1*h+S2*h+S3*h==h(S1+S2+S3)=S*hS1S2S3hОбъем наклонной призмы равен произведению бокового ребра
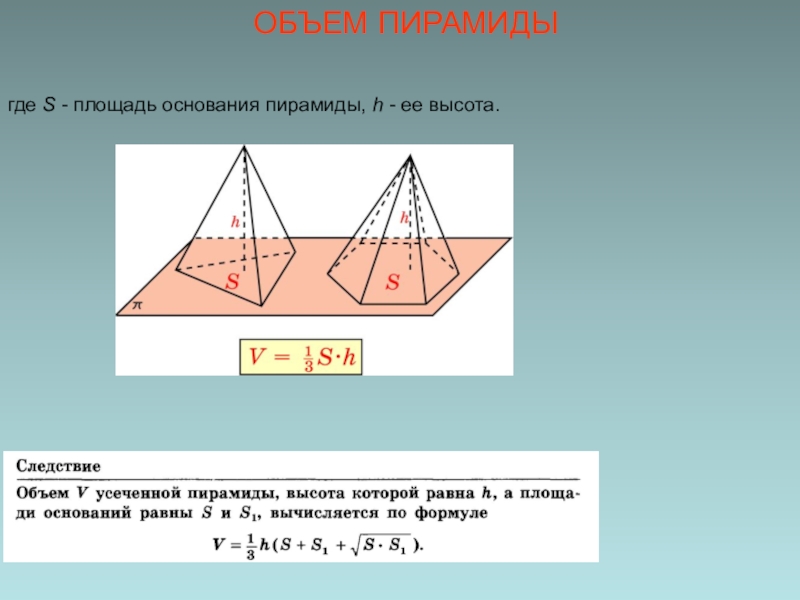
- 12. ОБЪЕМ ПИРАМИДЫгде S - площадь основания пирамиды, h - ее высота.
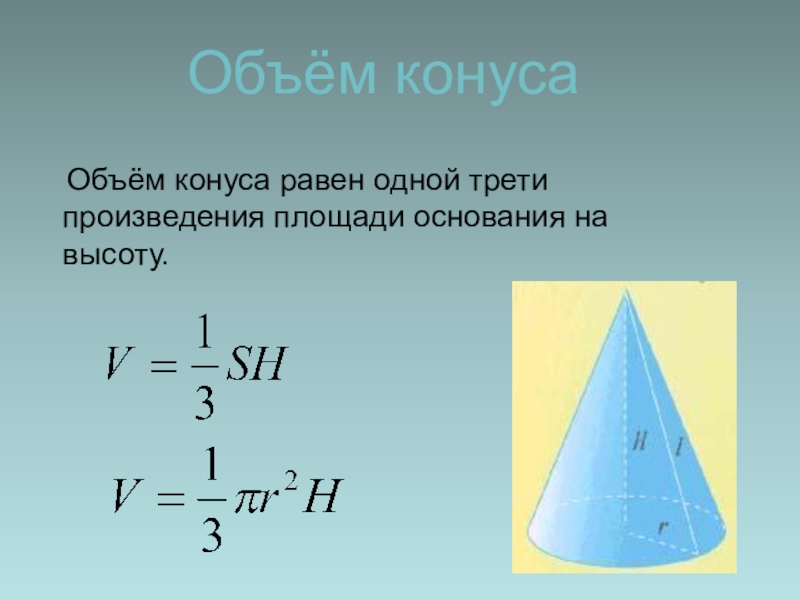
- 13. Объём конуса Объём конуса равен одной трети произведения площади основания на высоту.
- 14. Объём усечённого конуса
- 15. Объём шара Объём шара равен
- 16. Шаровой сегментШаровым сегментом называется часть шара, отсекаемая от него плоскостью.
- 17. Объём шарового сегментаОбъём шарового сегмента равен Здесь
- 18. ШАРОВОЙ СЛОЙШаровой слой – часть шара, заключенная между двумя параллельными секущими плоскостями.
- 19. ШАРОВОЙ СЕКТОР
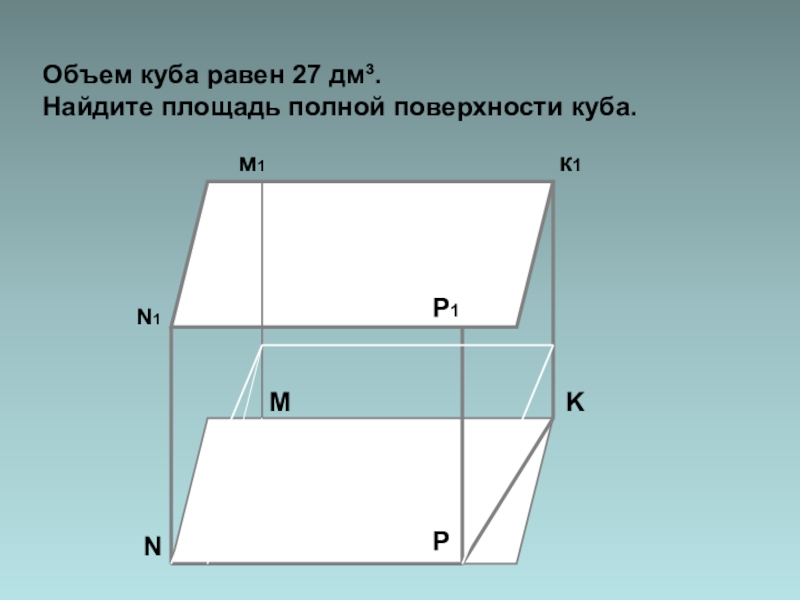
- 20. NN1Kк1м1PP1MОбъем куба равен 27 дм³. Найдите площадь полной поверхности куба.
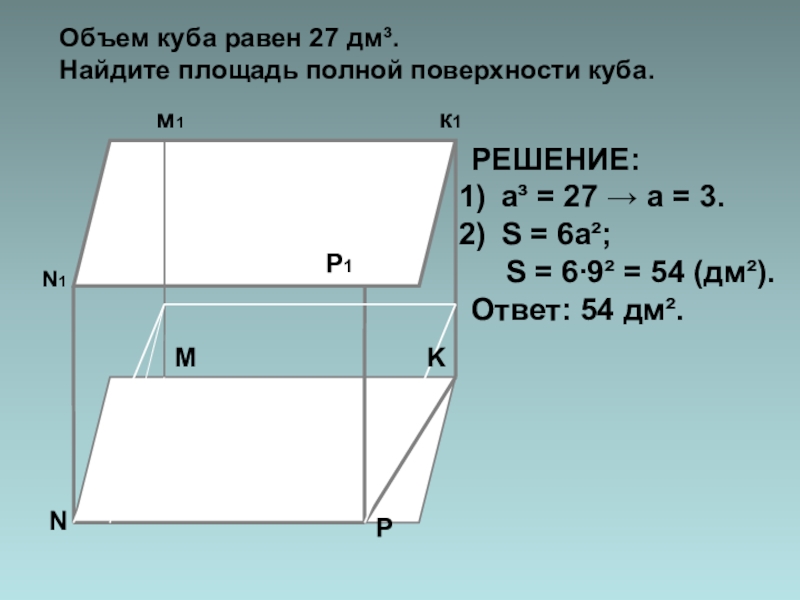
- 21. NN1Kк1м1PP1MРЕШЕНИЕ:а³ = 27 → а = 3.S
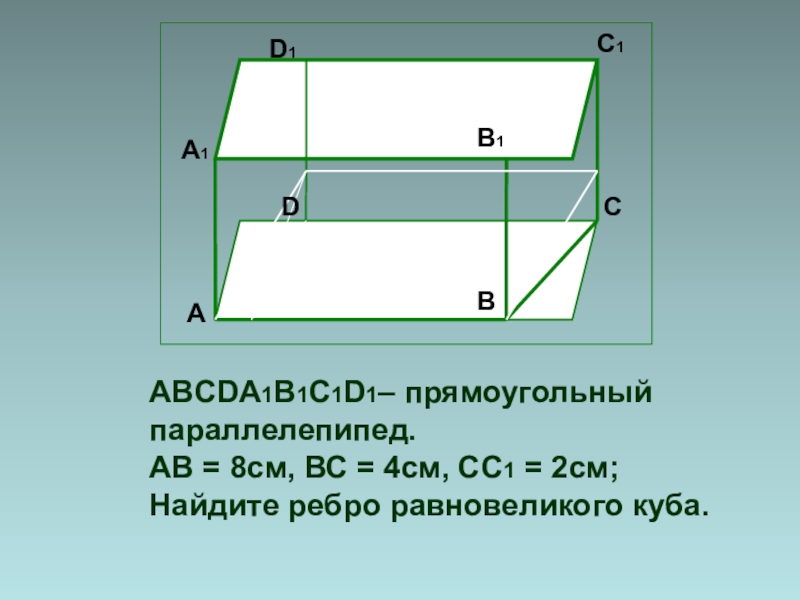
- 22. ABCDA1B1C1D1– прямоугольный параллелепипед.АВ = 8см, ВС = 4см, СС1 = 2см;Найдите ребро равновеликого куба.АА1В1D1DC1BC
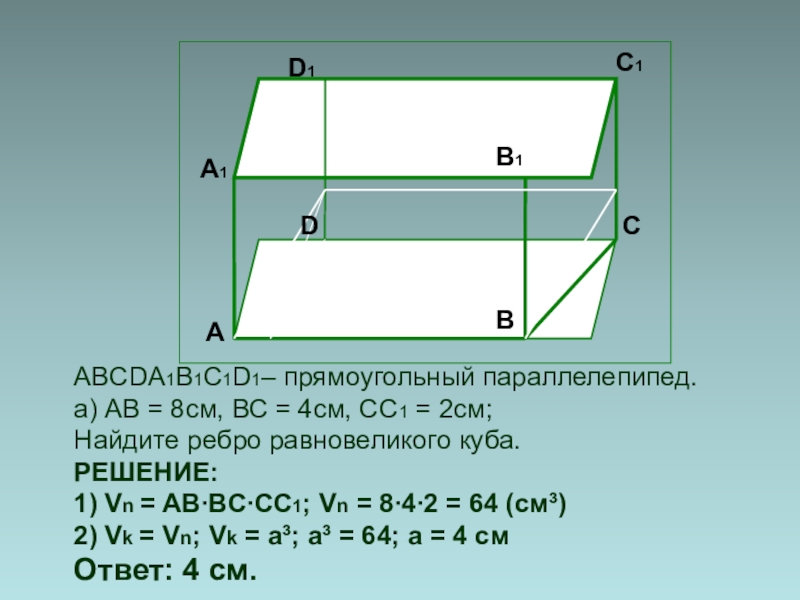
- 23. ABCDA1B1C1D1– прямоугольный параллелепипед.а) АВ = 8см, ВС
- 24. Домашнее заданиеП.74 – 83, № 648 а,в; 650, 653
- 25. В цилиндр, радиус основания
- 26. Зад. № 671г) Дано: Цилиндр, вписанная n-угольная призма, n=8.Найти: Vпр./ Vцил. Решение:
Подведение итогов В) S = 2πRhД) S = 2πR(R+h)Г) S = πRlА) S = πR( R+l )Б) S = 4πR2123О
Слайд 1Понятие объема.
Объемы геометрических фигур
Геометрия,
11 класс
Плужникова И. Ю
. учитель математики МАОУ
Слайд 3
Любое геометрическое тело в пространстве характеризуется величиной, называемой ОБЪЕМОМ. Так что
же такое – объем пространственной фигуры?
Под объемом пространственной фигуры понимается положительная величина, обладающая следующими свойствами:
равные фигуры имеют равные объемы;
объем фигуры равен сумме объемов ее частей;
объем куба с ребром единичной длины равен одной кубической единице.
Если одно тело содержит другое, то объем первого тела не меньше объема второго.
V1=V2
V=V1+V2+V3
V=1 куб.ед.
Слайд 4a
b
c=H
a×b×c
Самым естественным образом определяется объем прямоугольного параллелепипеда, как геометрического тела составленного
из определенного количества единичных кубов. А значит, его объем определяется как сумма объемов этих единичных кубов.
Слайд 5ABCDA1B1C1D1–прямоугольный параллелепипед
а) V = a²h
б) V = 1/2d²b
в) V = abc
г)
V = 1/2d²bsinφ
В1
В1
С1
С1
А1
А1
D1
D1
D1
D1
А1
А1
В1
В1
С1
С1
С
С
С
С
А
А
А
А
В
В
В
В
D
D
D
D
1)
2)
3)
4)
а
с
h
d
b
b
d
φ
b
а
а
Слайд 6Объём прямоугольного параллелепипеда
Теорема: объём прямоугольного параллелепипеда равен произведению трёх его измерений.
a,b,c – измерения прямоугольного параллелепипеда.
V = abc.
Следствие 1: объём прямоугольного параллелепипеда равен произведению площади основания на высоту.
V = abc=Sh.
V = abc.
Следствие 1: объём прямоугольного параллелепипеда равен произведению площади основания на высоту.
V = abc=Sh.
Слайд 7Следствие 2.
Объём прямой призмы, основанием которой является прямоугольный треугольник, равен произведению
площади основания на высоту.
V = SABCh.
V = SABCh.
Слайд 9
Итак, для любой n-угольной призмы:
ИЛИ
,где Sосн. – площадь основания призмы, S⊥сеч.
– площадь перпендикулярного сечения, H – высота призмы, m – длина бокового ребра призмы.
Слайд 11
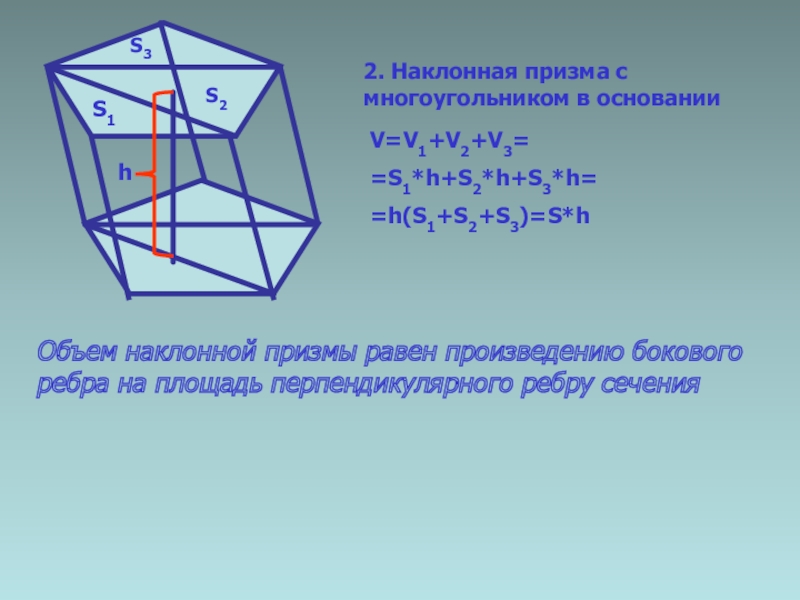
V=V1+V2+V3=
=S1*h+S2*h+S3*h=
=h(S1+S2+S3)=S*h
S1
S2
S3
h
Объем наклонной призмы равен произведению бокового ребра на площадь перпендикулярного ребру
сечения
2. Наклонная призма с многоугольником в основании
Слайд 17Объём шарового сегмента
Объём шарового сегмента равен
Здесь R – радиус шара,
а H – высота шарового сегмента.
Слайд 18ШАРОВОЙ СЛОЙ
Шаровой слой – часть шара, заключенная между двумя параллельными секущими
плоскостями.
Слайд 21N
N1
K
к1
м1
P
P1
M
РЕШЕНИЕ:
а³ = 27 → а = 3.
S = 6а²;
S = 6∙9² = 54 (дм²).
Ответ: 54 дм².
Ответ: 54 дм².
Объем куба равен 27 дм³.
Найдите площадь полной поверхности куба.
Слайд 22ABCDA1B1C1D1– прямоугольный параллелепипед.
АВ = 8см, ВС = 4см, СС1 = 2см;
Найдите
ребро равновеликого куба.
А
А1
В1
D1
D
C1
B
C
Слайд 23ABCDA1B1C1D1– прямоугольный параллелепипед.
а) АВ = 8см, ВС = 4см, СС1 =
2см;
Найдите ребро равновеликого куба.
РЕШЕНИЕ:
1) Vn = AB∙BC∙CC1; Vn = 8∙4∙2 = 64 (см³)
2) Vk = Vn; Vk = a³; a³ = 64; a = 4 см
Ответ: 4 см.
Найдите ребро равновеликого куба.
РЕШЕНИЕ:
1) Vn = AB∙BC∙CC1; Vn = 8∙4∙2 = 64 (см³)
2) Vk = Vn; Vk = a³; a³ = 64; a = 4 см
Ответ: 4 см.
А
А1
В1
D1
D
C1
B
C
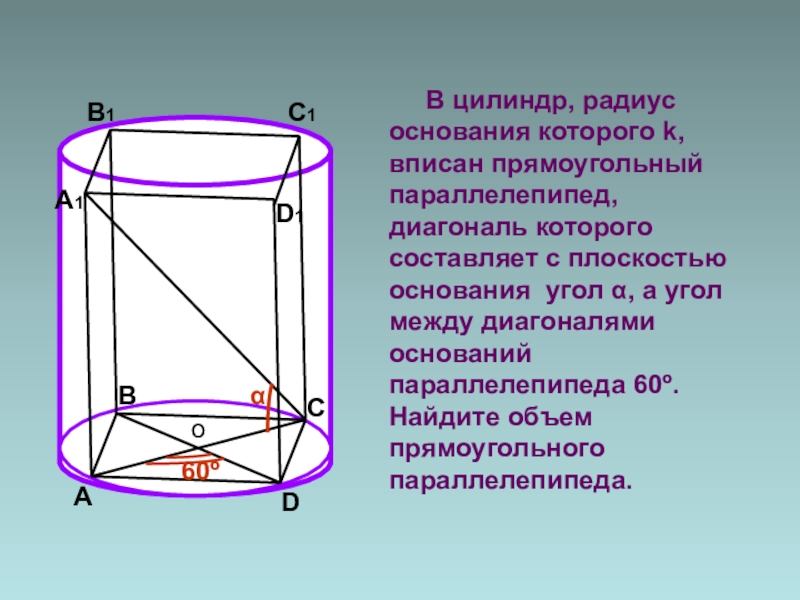
Слайд 25 В цилиндр, радиус основания которого k, вписан прямоугольный
параллелепипед, диагональ которого составляет с плоскостью основания угол α, а угол между диагоналями оснований параллелепипеда 60º. Найдите объем прямоугольного параллелепипеда.
В1
C1
A
A1
D1
В
C
D
α
60º
о
Слайд 26Зад. № 671г)
Дано: Цилиндр, вписанная n-угольная призма, n=8.
Найти: Vпр./
Vцил.
Решение: <ВОС= 3600/8 = 450. SВОС=1/2ОВ*ОС*sin<ВОС=1/2r2*sin45=1/2r2 √2/2=r2√2/4.
Sосн.пр.=8SВОС=8r2√2/4=2r2√2.
Vпр.=Sосн*h=2r2h√2
Vцил.=Пr2h. Vпр./Vцил.=2√2/П
Ответ: 2√2/П
К
r
С
В
О
