- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Некоторые свойства прямоугольных треугольников (7 класс)
Содержание
- 1. Презентация по геометрии на тему Некоторые свойства прямоугольных треугольников (7 класс)
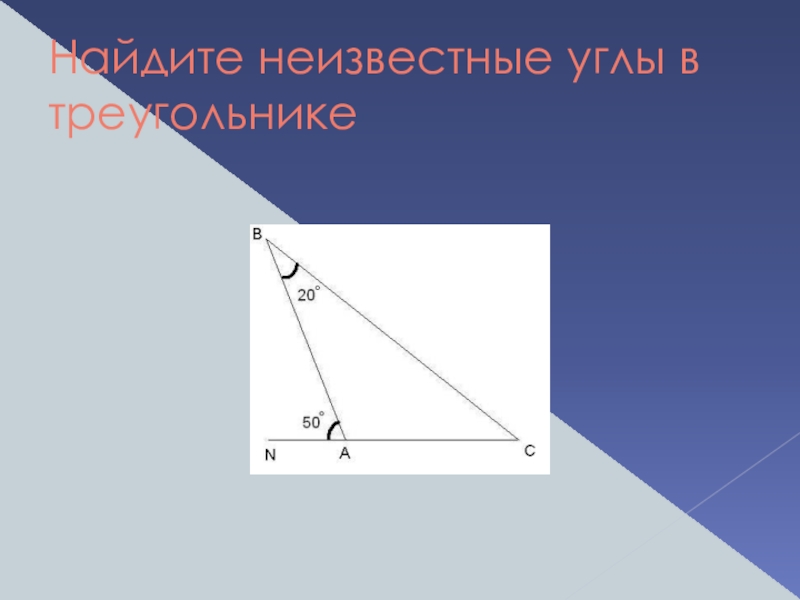
- 2. Найдите неизвестные углы в треугольнике
- 3. Найдите неизвестные углы в треугольнике
- 4. Найдите неизвестные углы в треугольнике
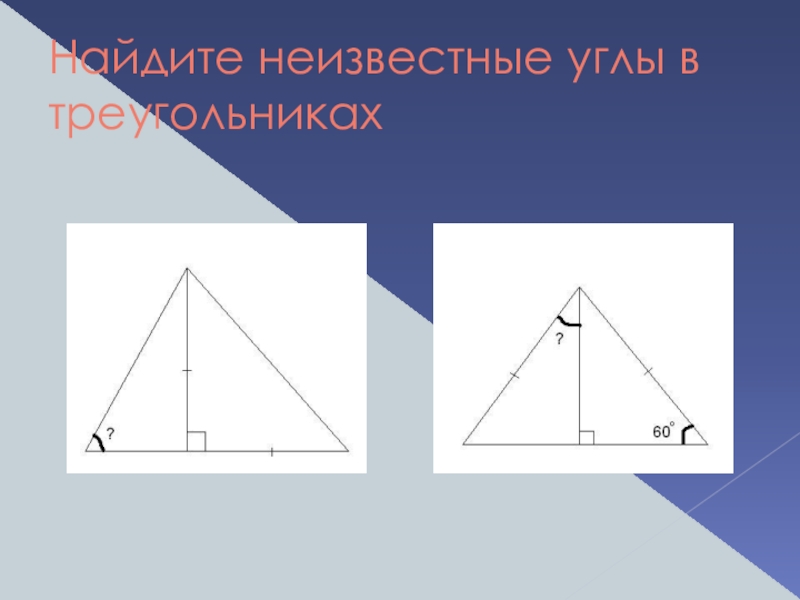
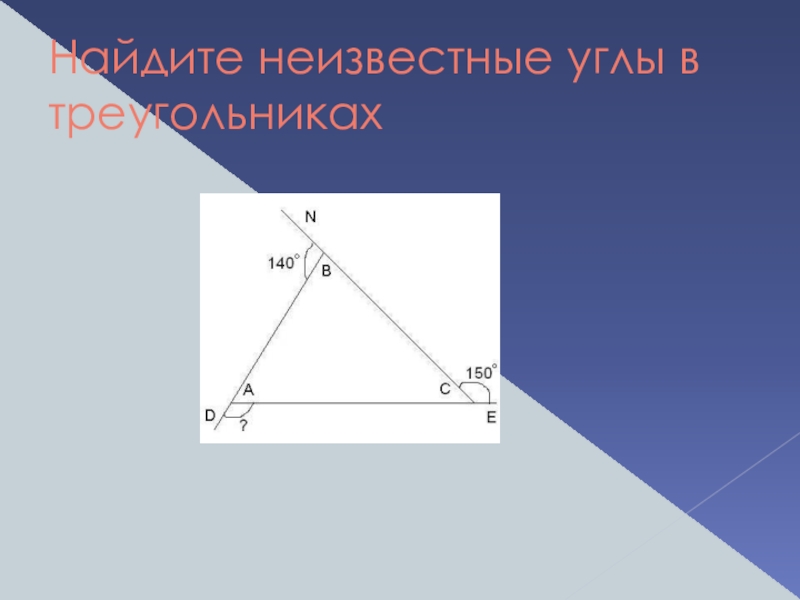
- 5. Найдите неизвестные углы в треугольниках
- 6. Найдите неизвестные углы в треугольниках
- 7. Свойство1. Сумма двух острых углов прямоугольного треугольника равна 90º.Дано: ∆ ABC; ∟C=90º.Доказать: ∟A+∟B=90º
- 8. Свойство1. Сумма двух острых углов прямоугольного треугольника
- 9. Свойство 2. Катет прямоугольного треугольника, лежащего
- 10. Дано: ∆ ABC; ∟C=90º, ∟В=30ºДоказать: Доказательство:1) Достроим к ∆ACB ∆DCB = ∆ ACB.
- 11. Дано: ∆ ABC; ∟C=90º, ∟В=30ºДоказать: Доказательство:Достроим
- 12. Свойство 3. Если катет прямоугольного треугольника равен
- 13. Дано: ∆АВС,∟А=90º,
- 14. Дано: ∆АВС,∟А=90º,
- 15. №255. В равнобедренном треугольнике CDE с основанием
- 16. Дано: ∆CDE - равнобедренный;
- 17. №257. В прямоугольном треугольнике ABC с прямым
- 18. Дано: ∆АВС; ∟С=90º.
- 19. Дано: ∆АВС; ∟С=90º.
- 20. 3.
- 21. №260 Высота, проведенная к основанию равнобедренного треугольника,
- 22. Решение:1. Из условия мы видим
Найдите неизвестные углы в треугольнике
Слайд 1Некоторые свойства прямоугольных треугольников.
Подготовила : Чайкина И.В., учитель математики
Тема урока:
Слайд 7Свойство1.
Сумма двух острых углов прямоугольного треугольника равна 90º.
Дано:
∆ ABC;
∟C=90º.
Доказать: ∟A+∟B=90º
Доказать: ∟A+∟B=90º
Слайд 8Свойство1.
Сумма двух острых углов прямоугольного треугольника равна 90º.
Дано:
∆ ABC;
∟C=90º.
Доказать: ∟A+∟B=90º
Доказательство:
∟A+ ∟B+ ∟C=180º следовательно
∟A+ ∟B=180º–∟С; ∟A+ ∟B=90º
Доказать: ∟A+∟B=90º
Доказательство:
∟A+ ∟B+ ∟C=180º следовательно
∟A+ ∟B=180º–∟С; ∟A+ ∟B=90º
Слайд 9Свойство 2. Катет прямоугольного треугольника, лежащего против угла в 30º, равен
половине гипотенузы.
Дано:
∆ ABC; ∟C=90º, ∟В=30º
Доказать: .
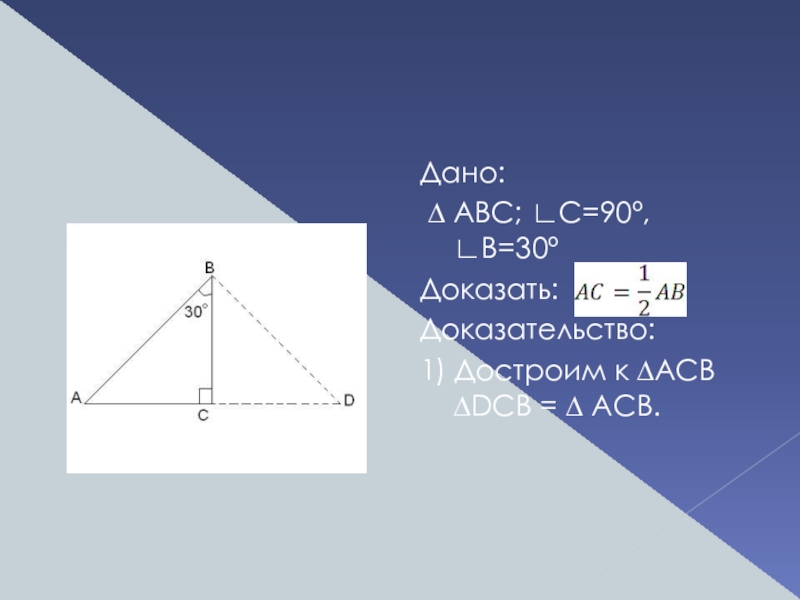
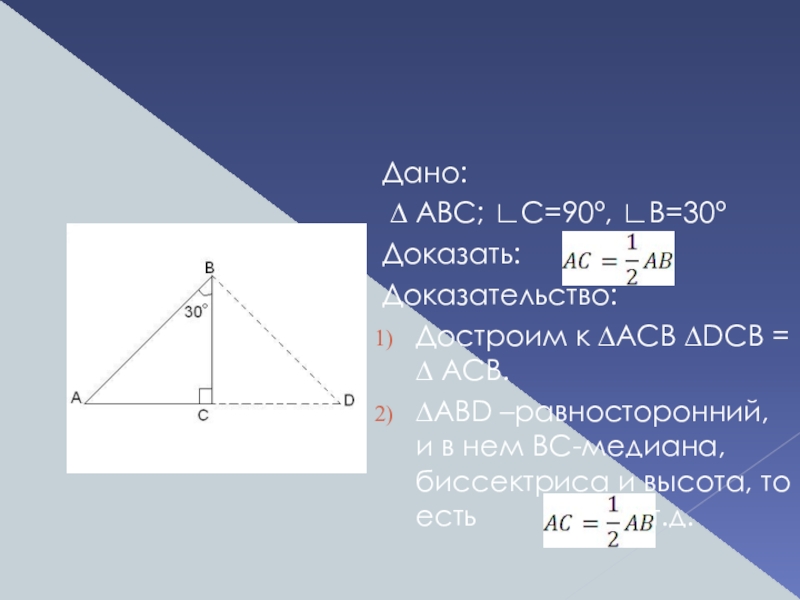
Слайд 11
Дано:
∆ ABC; ∟C=90º, ∟В=30º
Доказать:
Доказательство:
Достроим к ∆ACB ∆DCB
= ∆ ACB.
∆ABD –равносторонний, и в нем BC-медиана, биссектриса и высота, то есть , ч.т.д.
∆ABD –равносторонний, и в нем BC-медиана, биссектриса и высота, то есть , ч.т.д.
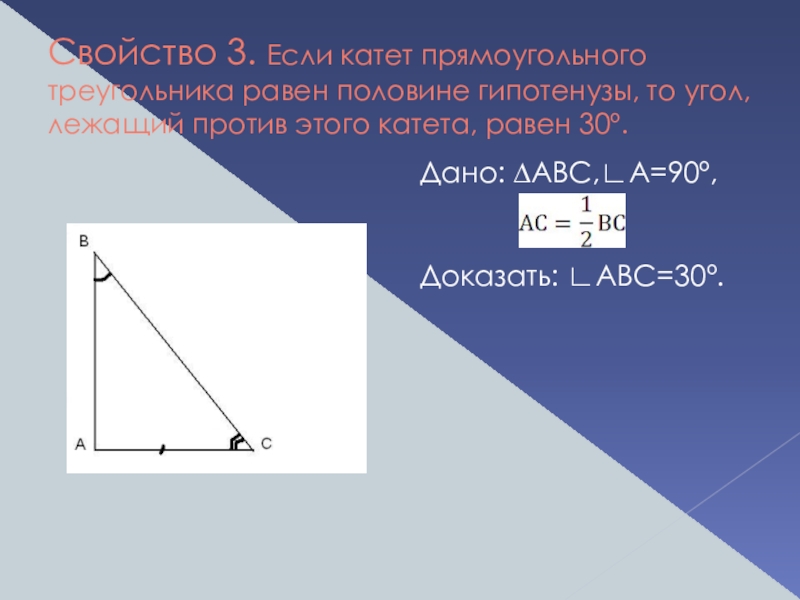
Слайд 12Свойство 3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол,
лежащий против этого катета, равен 30º.
Дано: ∆АВС,∟А=90º,
Доказать: ∟ABС=30º.
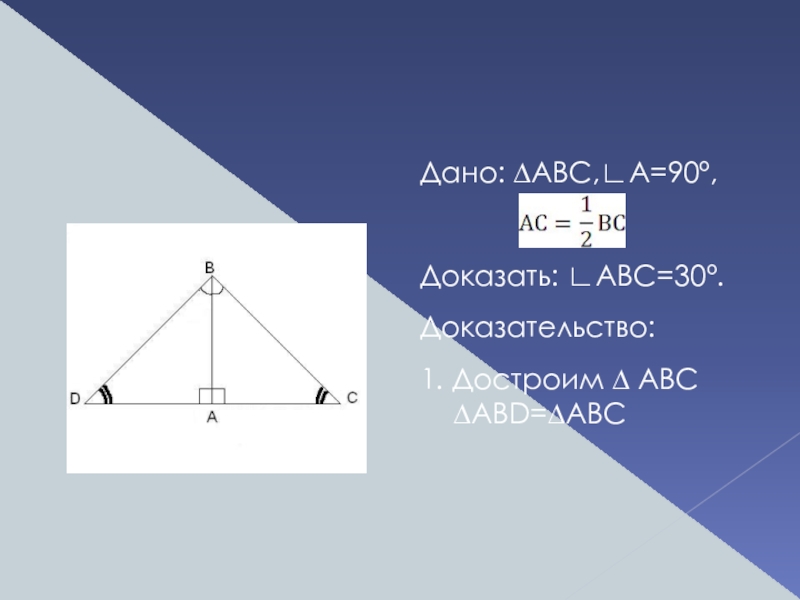
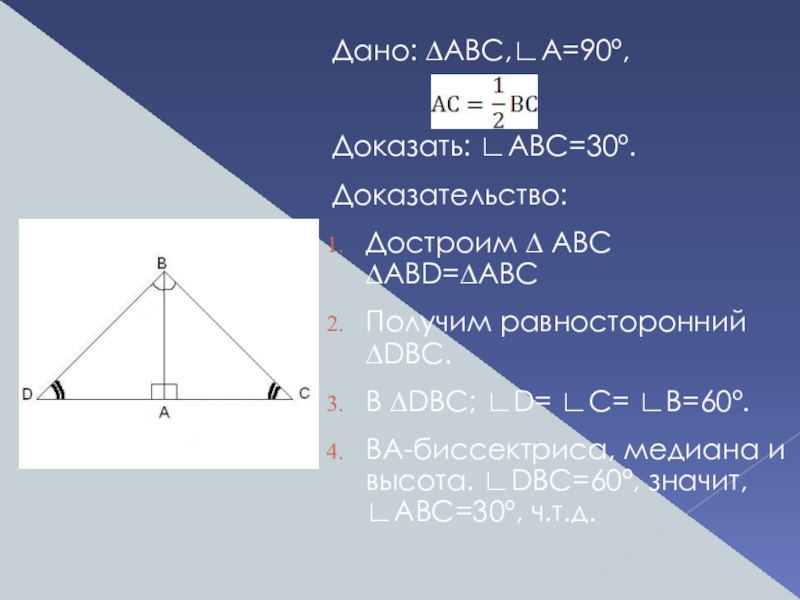
Слайд 14
Дано: ∆АВС,∟А=90º,
Доказать: ∟ABС=30º.
Доказательство:
Достроим ∆ ABC ∆ABD=∆ABC
Получим равносторонний ∆DBC.
В ∆DBC; ∟D= ∟C= ∟B=60º.
BA-биссектриса, медиана и высота. ∟DBC=60º, значит, ∟ABC=30º, ч.т.д.
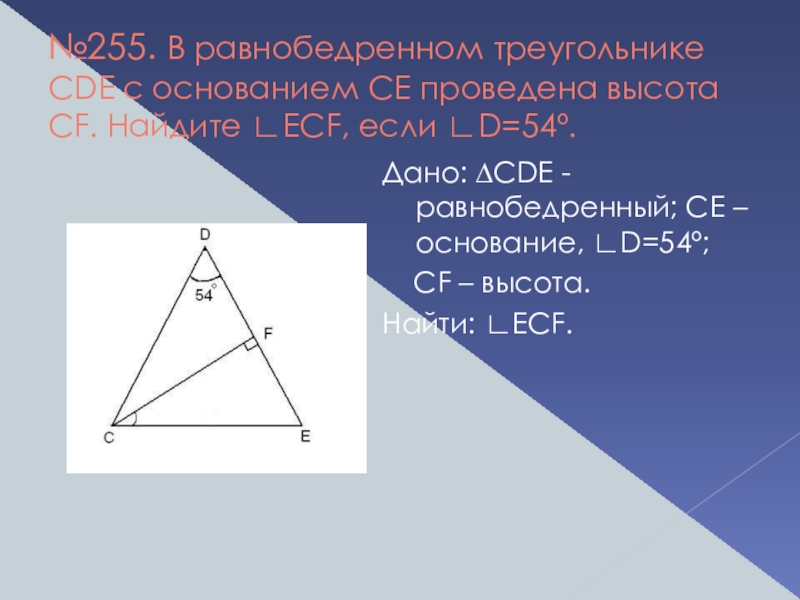
Слайд 15№255. В равнобедренном треугольнике CDE с основанием CE проведена высота CF.
Найдите ∟ECF, если ∟D=54º.
Дано: ∆CDE - равнобедренный; CE – основание, ∟D=54º;
CF – высота.
Найти: ∟ECF.
Слайд 16
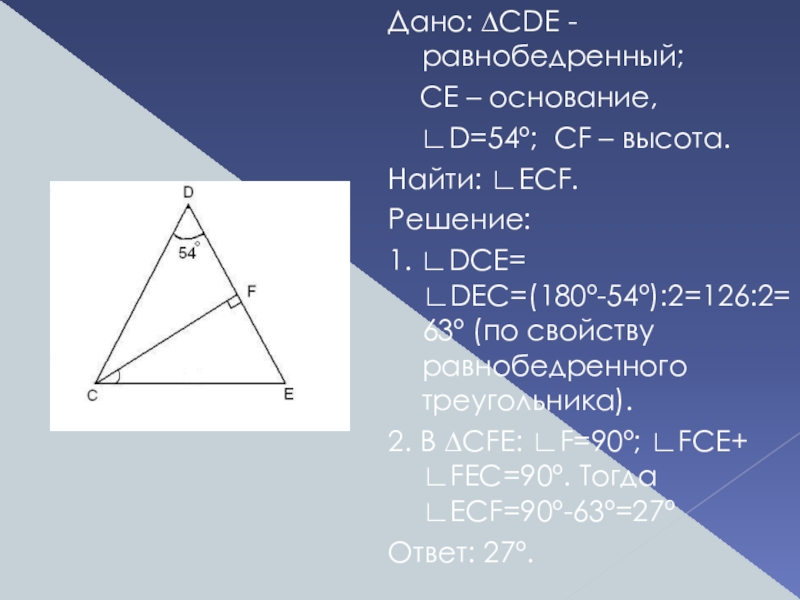
Дано: ∆CDE - равнобедренный;
CE – основание,
∟D=54º; CF – высота.
Найти: ∟ECF.
Решение:
1. ∟DCE= ∟DEC=(180º-54º):2=126:2=63º (по свойству равнобедренного треугольника).
2. В ∆CFE: ∟F=90º; ∟FCE+ ∟FEC=90º. Тогда ∟ECF=90º-63º=27º
Ответ: 27º.
Найти: ∟ECF.
Решение:
1. ∟DCE= ∟DEC=(180º-54º):2=126:2=63º (по свойству равнобедренного треугольника).
2. В ∆CFE: ∟F=90º; ∟FCE+ ∟FEC=90º. Тогда ∟ECF=90º-63º=27º
Ответ: 27º.
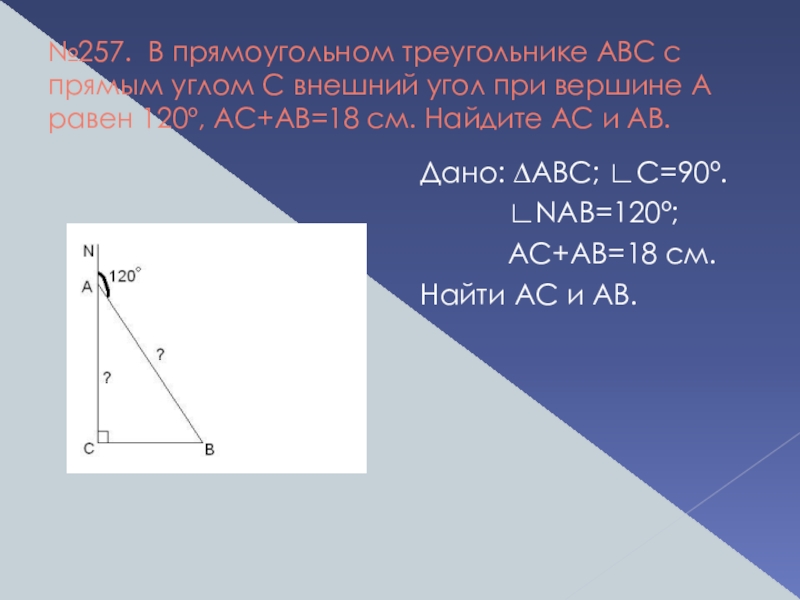
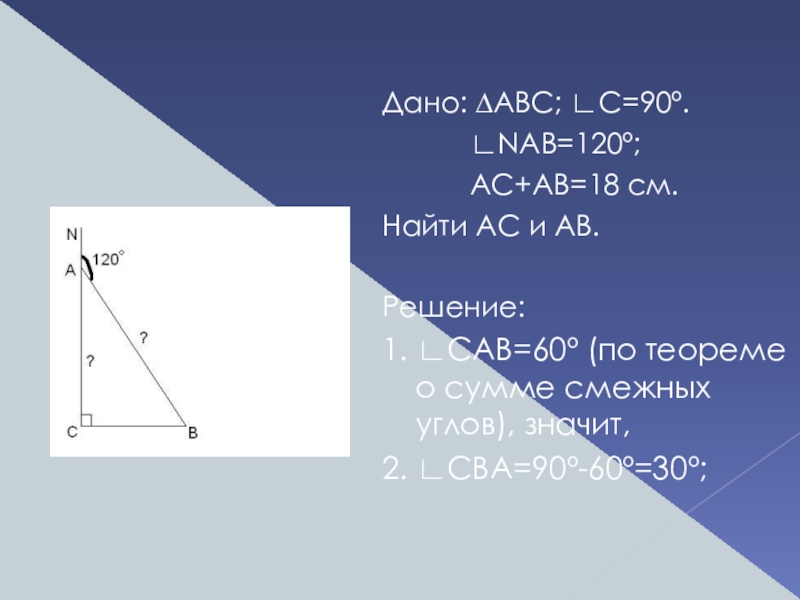
Слайд 17№257. В прямоугольном треугольнике ABC с прямым углом С внешний угол
при вершине А равен 120º, АС+АВ=18 см. Найдите АС и АВ.
Дано: ∆АВС; ∟С=90º.
∟NAB=120º;
AC+AB=18 см.
Найти АС и АВ.
Слайд 19
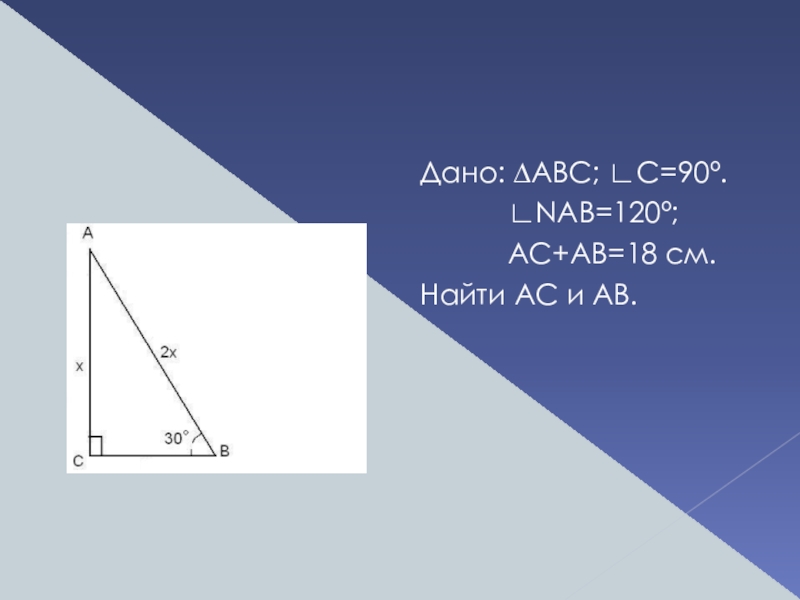
Дано: ∆АВС; ∟С=90º.
∟NAB=120º;
AC+AB=18 см.
Найти АС и АВ.
Решение:
1. ∟САВ=60º (по теореме о сумме смежных углов), значит,
2. ∟СВА=90º-60º=30º;
Найти АС и АВ.
Решение:
1. ∟САВ=60º (по теореме о сумме смежных углов), значит,
2. ∟СВА=90º-60º=30º;
Слайд 20
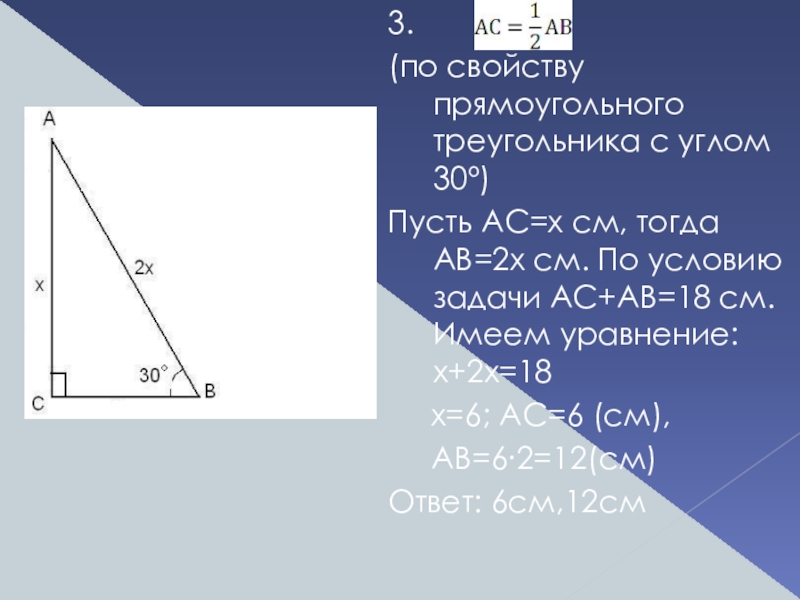
3.
(по
свойству прямоугольного треугольника с углом 30º)
Пусть АС=x см, тогда АВ=2x см. По условию задачи AC+AB=18 см. Имеем уравнение: x+2x=18
x=6; АС=6 (см),
АВ=6∙2=12(см)
Ответ: 6см,12см
Пусть АС=x см, тогда АВ=2x см. По условию задачи AC+AB=18 см. Имеем уравнение: x+2x=18
x=6; АС=6 (см),
АВ=6∙2=12(см)
Ответ: 6см,12см
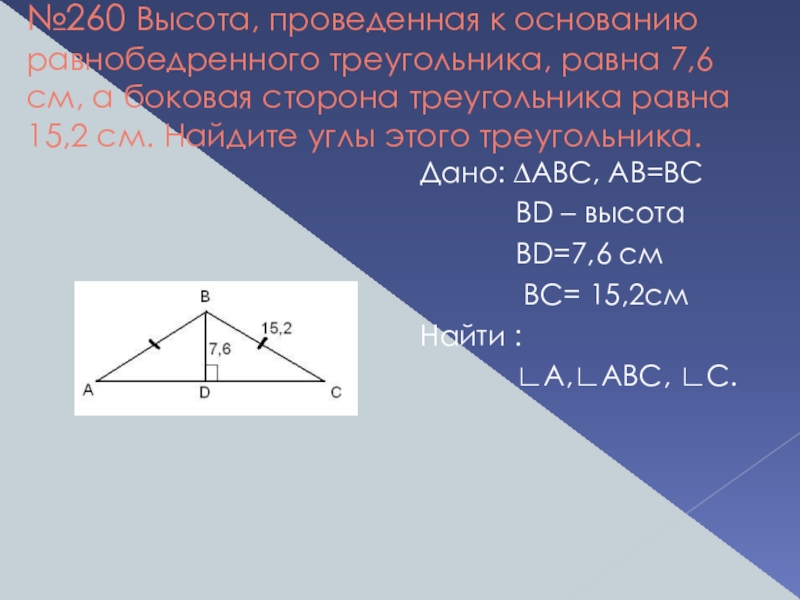
Слайд 21№260 Высота, проведенная к основанию равнобедренного треугольника, равна 7,6 см, а
боковая сторона треугольника равна 15,2 см. Найдите углы этого треугольника.
Дано: ∆АВС, AB=BC
BD – высота
BD=7,6 см
ВС= 15,2см
Найти :
∟A,∟ABC, ∟C.
Слайд 22
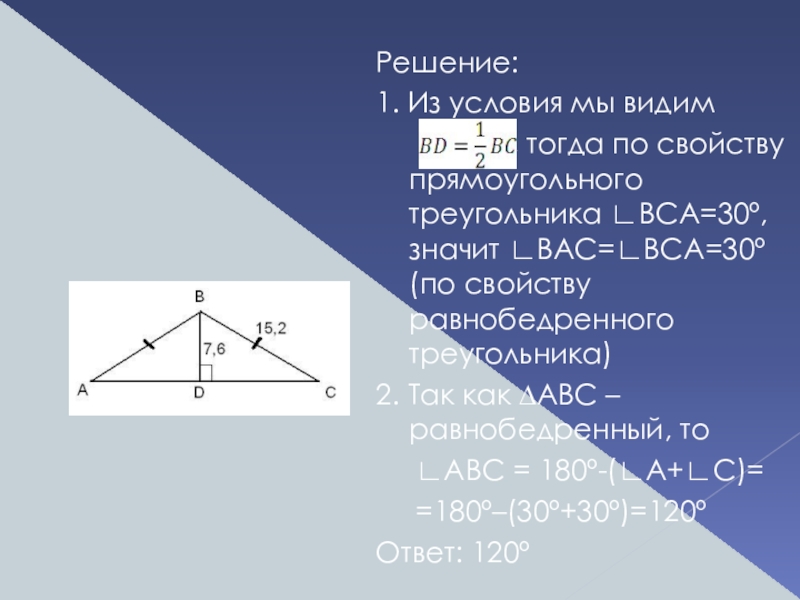
Решение:
1. Из условия мы видим
, тогда по свойству прямоугольного треугольника ∟BCA=30º, значит ∟BAC=∟BCA=30º (по свойству равнобедренного треугольника)
2. Так как ∆ABC – равнобедренный, то
∟ABC = 180º-(∟A+∟C)=
=180º–(30º+30º)=120º
Ответ: 120º
