- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Некоторые свойства прямоугольных треугольников (7 класс)
Содержание
- 1. Презентация по геометрии на тему Некоторые свойства прямоугольных треугольников (7 класс)
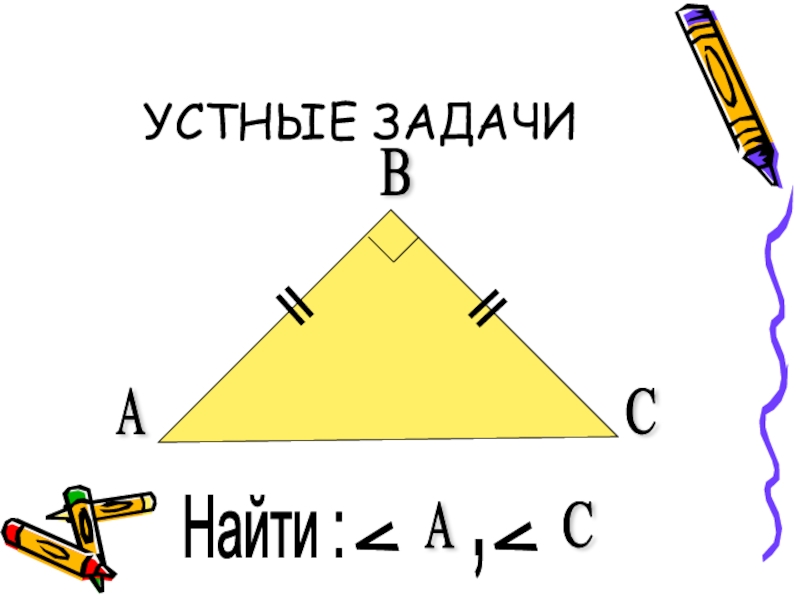
- 2. УСТНЫЕ ЗАДАЧИАСВ==Найти :^^АС,
- 3. НАЙТИ НЕИЗВЕСТНЫЕ УГЛЫ50°??АВСD
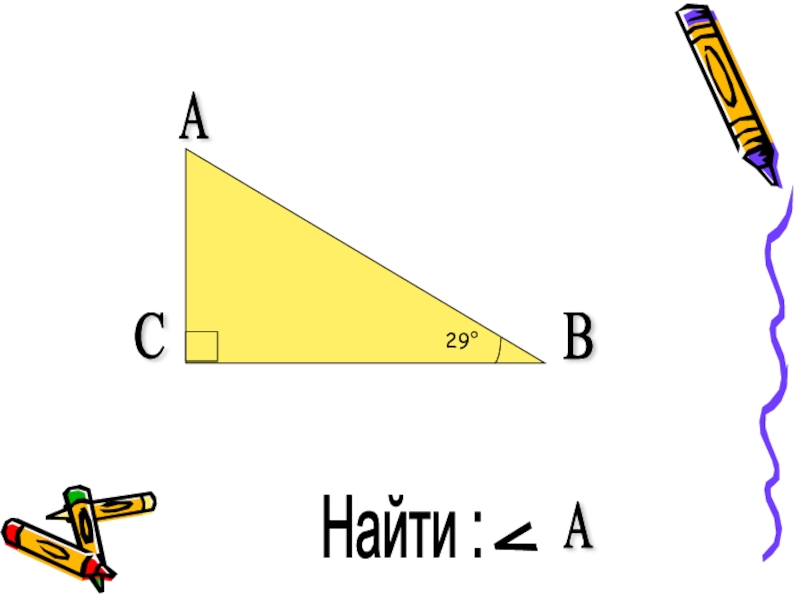
- 4. Найти :^АВСА29°
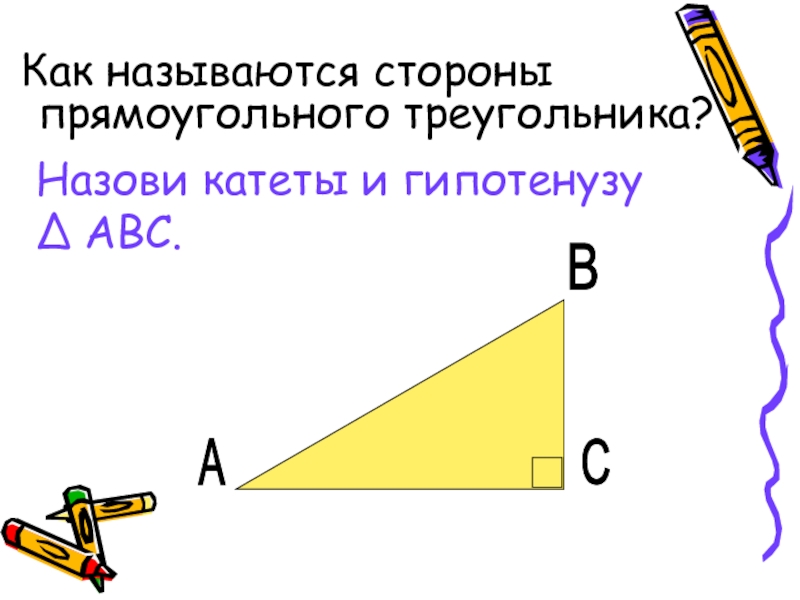
- 5. Как называются стороны прямоугольного
- 6. НЕКОТОРЫЕ СВОЙСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ.
- 7. СВОЙСТВО 1 В прямоугольном треугольнике сумма острых углов равна 90°
- 8. АСВﮮА + ﮮВ = 90°Так как ﮮА
- 9. СВОЙСТВО 2 Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
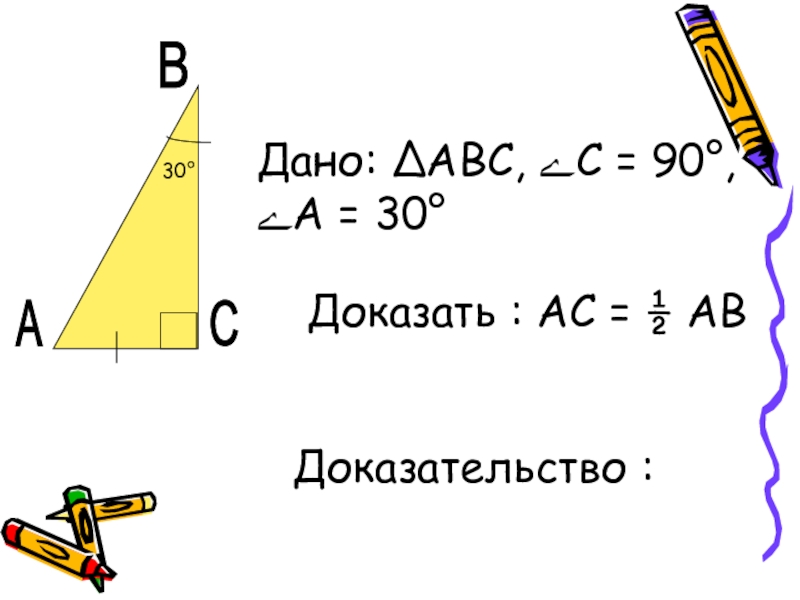
- 10. ВСАДано: ∆АВС, ﮮС = 90°, ﮮА = 30°Доказать : АС = ½ АВДоказательство :30°
- 11. ДОКАЗАТЕЛЬСТВО:30°АВСD∆АВС : ﮮА = 90° - ﮮВ
- 12. СВОЙСТВО 3 Если катет прямоугольного
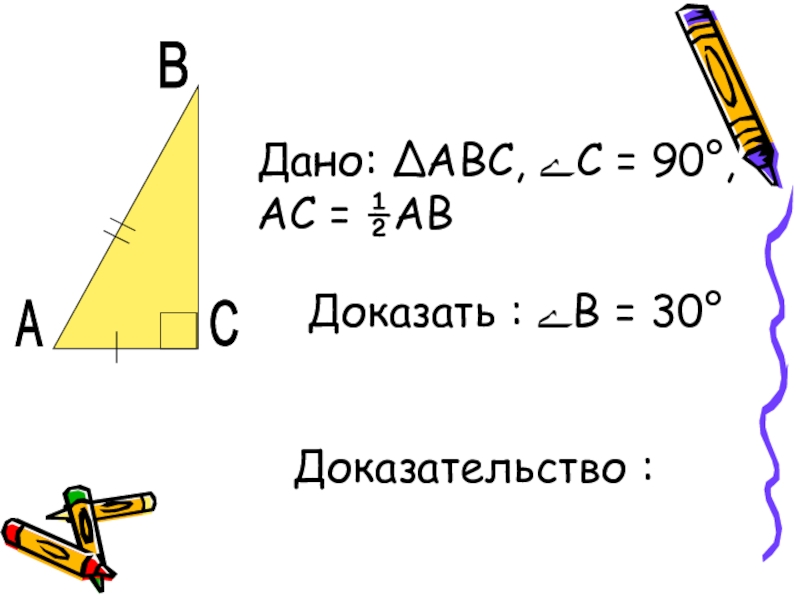
- 13. ВСАДано: ∆АВС, ﮮС = 90°, АС = ½АВДоказать : ﮮВ = 30°Доказательство :
- 14. ДОКАЗАТЕЛЬСТВО:АВСD∆АВС : АС = ½АВ, АВ =
- 15. ЗАДАНИЕ НА ДОМ§ 3, п. 34, Вопросы: 10 – 11,№ 254, № 256
- 16. РЕШАЕМ В ТЕТРАДИ№ 255DFEСДано: ∆СDЕ: СD =
- 17. В С Е М С П А С И Б О
УСТНЫЕ ЗАДАЧИАСВ==Найти :^^АС,
Слайд 9СВОЙСТВО 2
Катет прямоугольного треугольника, лежащий против угла в 30°,
равен половине гипотенузы.
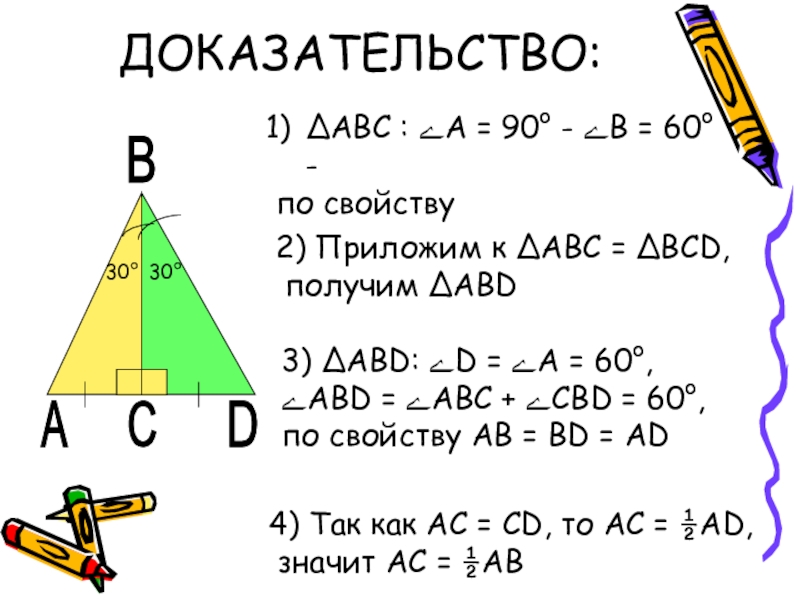
Слайд 11ДОКАЗАТЕЛЬСТВО:
30°
А
В
С
D
∆АВС : ﮮА = 90° - ﮮВ = 60°-
по свойству
2)
Приложим к ∆АВС = ∆ВСD,
получим ∆ABD
получим ∆ABD
3) ∆ABD: ﮮD = ﮮА = 60°, ﮮАВD = ﮮАВС + ﮮСВD = 60°, по свойству АВ = ВD = АD
4) Так как АС = CD, то АС = ½АD,
значит АС = ½АВ
30°
Слайд 12
СВОЙСТВО 3
Если катет прямоугольного треугольника равен половине гипотенузы, то
угол, лежащий против этого катета, равен 30°.
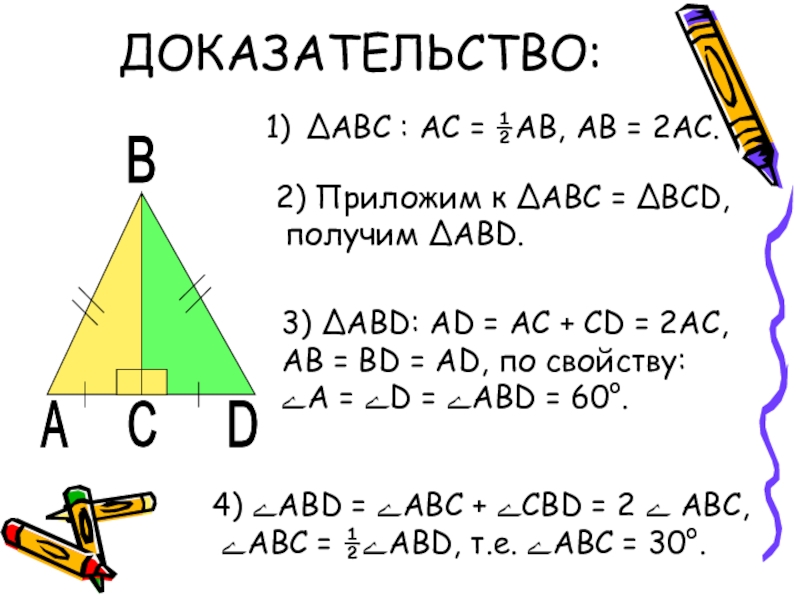
Слайд 14ДОКАЗАТЕЛЬСТВО:
А
В
С
D
∆АВС : АС = ½АВ, АВ = 2АС.
2) Приложим к ∆АВС
= ∆ВСD,
получим ∆ABD.
получим ∆ABD.
3) ∆ABD: АD = АС + СD = 2АС, АВ = ВD = АD, по свойству:
ﮮА = ﮮD = ﮮАВD = 60°.
4) ﮮАВD = ﮮАВС + ﮮСВD = 2 ﮮ АВС,
ﮮАВС = ½ﮮАВD, т.е. ﮮАВС = 30°.
Слайд 16РЕШАЕМ В ТЕТРАДИ
№ 255
D
F
E
С
Дано: ∆СDЕ: СD = DЕ,
СF DЕ, ﮮD
= 54°
Найти: ﮮЕСF
Решение.
Рассм. ∆СDЕ: СD = DЕ, по свойству
ﮮDСЕ = ﮮDЕС = (180° - ﮮD) : 2 =
= (180° - 54°) : 2 = 63°.
2) Рассм. ∆ЕСF: ﮮСFЕ = 90°, ﮮСЕF = 63°,
По свойству ﮮЕСF + ﮮСЕF = 90°, значит
ﮮЕСF = 90° - ﮮСЕF = 90° - 63° = 27°
Ответ: ﮮЕСF = 27°.
54°
Т
