- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Многоугольники (9 класс)
Содержание
- 1. Презентация по геометрии на тему Многоугольники (9 класс)
- 2. I. Устная работа Определите какая из изображенных геометрических фигур лишняя?
- 3. Ломаные Ломаной называется …
- 4. Задание№11. Изобразите ломаную: а) простую незамкнутую; б)
- 5. Рис 1Рис 4Рис 2Рис 3- Чем отличаются
- 6. - Как назвать фигуру, состоящую из простой замкнутой ломаной и ограниченной ею внутренней областью плоскости? Многоугольник
- 7. Цель урока:Приобрести знания и умения по теме
- 8. Многоугольники Многоугольником называется …
- 9. Выпуклые и невыпуклые многоугольникиМногоугольник называется выпуклым, если
- 10. ВопросыКак называется длина ломаной, ограничивающей многоугольник?Каким образом можно сгруппировать изображенные многоугольники?
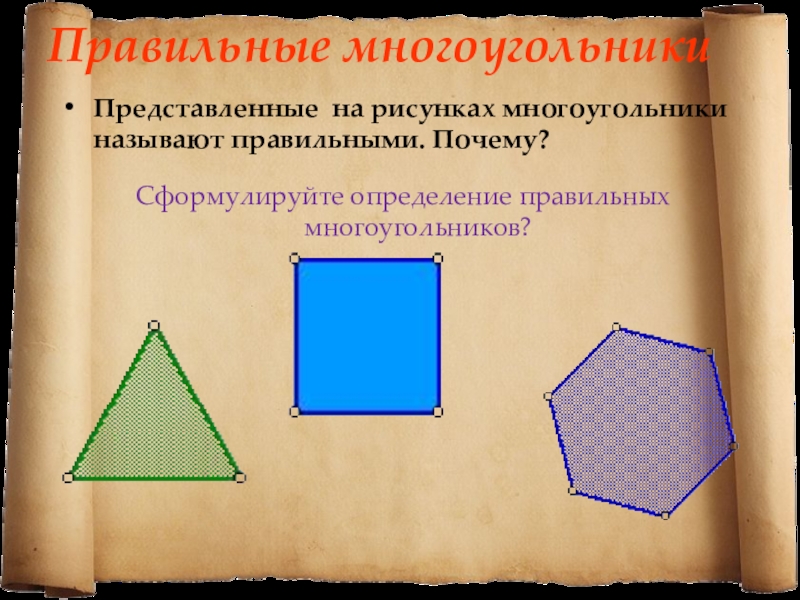
- 11. Правильные многоугольникиПредставленные на рисунках многоугольники называют правильными. Почему?Сформулируйте определение правильных многоугольников?
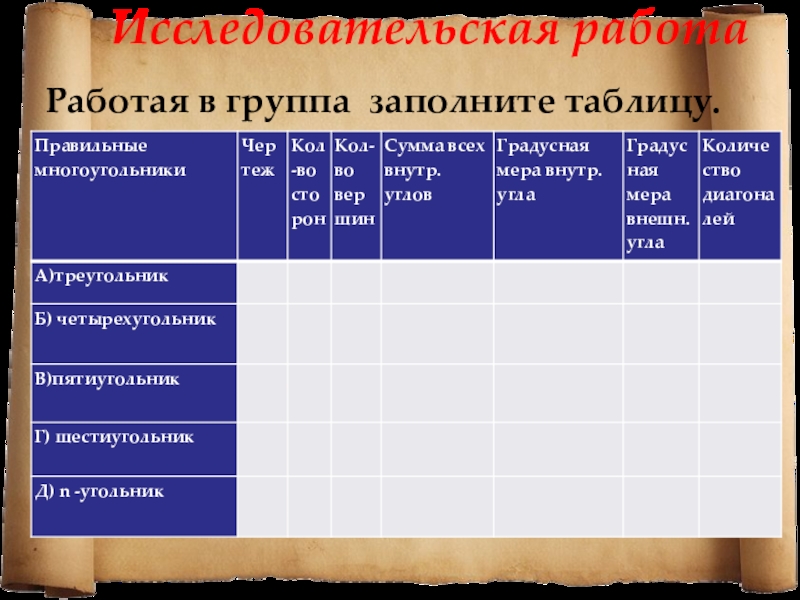
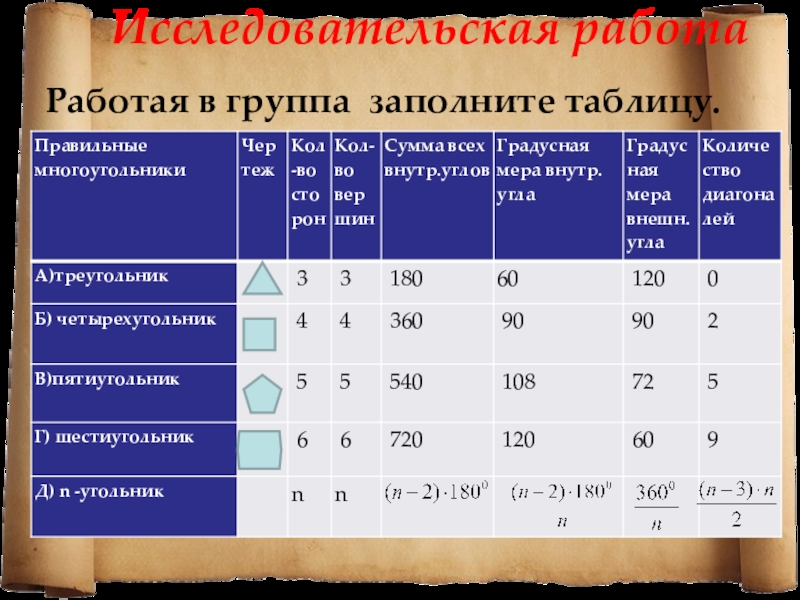
- 12. Исследовательская работаРаботая в группа заполните таблицу.
- 13. Исследовательская работаРаботая в группа заполните таблицу.
- 14. Великий математик, механик и инженер древности Архимед
- 15. Евклид ( родился в 330 году до
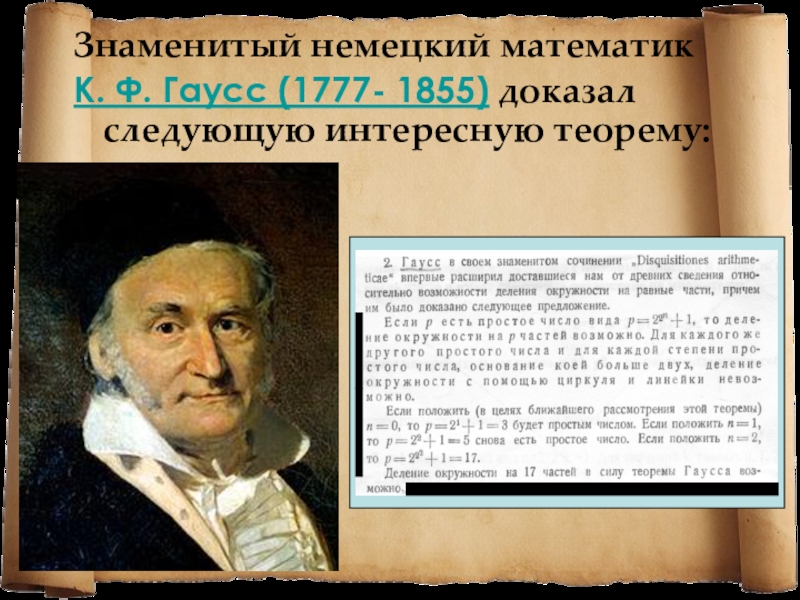
- 16. Знаменитый немецкий математик К. Ф. Гаусс (1777- 1855) доказал следующую интересную теорему:
- 17. Слайд 17
- 18. Слайд 18
- 19. Построение правильных многоугольников с помощью циркуля и
- 20. Слайд 20
- 21. А так ли уж важно изучать и
- 22. Пчелы – удивительные творения природы. Свои геометрические
- 23. Еще одна загадка природы:Почему в природе так часто встречаются шестиугольные формы?
- 24. Платоновы телаПлатоновы тела - трехмерный аналог плоских
- 25. Слайд 25
- 26. Многогранники в искусстве
- 27. Проект:Магический многоугольник
- 28. Слайд 28
- 29. Клуб исследователей по интересам «Историки» - изучение
- 30. Как мы будем работать в проекте?Работая
- 31. План-график работы
- 32. План-график сдачи творческих работ
- 33. РефлексияЗаполнить таблицу Знал – Интересно - Узнал:
- 34. Домашнее задание1) П.11 Группа А - №
- 35. Не закапывайте свой талант! Помни!1 из 1000
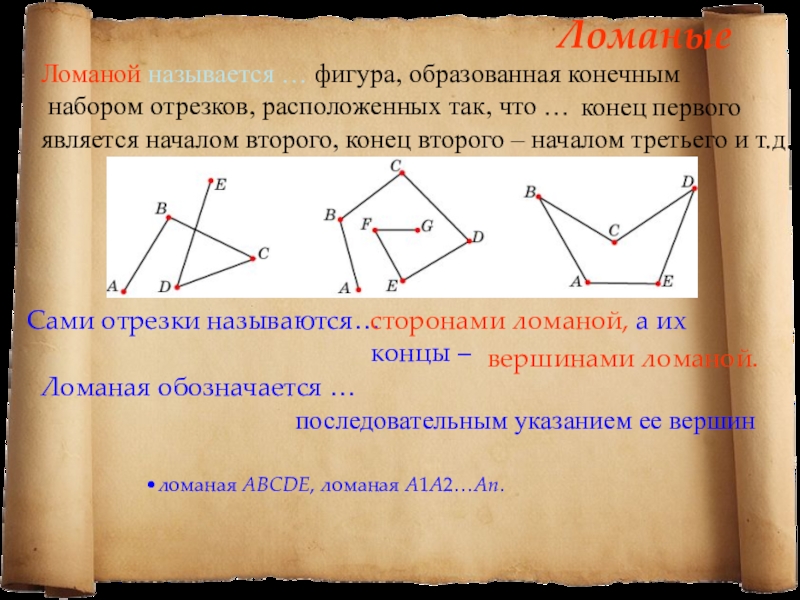
Слайд 3Ломаные
Ломаной называется …
Сами отрезки называются…
сторонами ломаной, а их концы –
конец первого является началом второго, конец второго – началом третьего и т.д.
вершинами ломаной.
Ломаная обозначается …
последовательным указанием ее вершин
ломаная АВСDE, ломаная A1A2…An.
Слайд 4Задание№1
1. Изобразите ломаную:
а) простую незамкнутую;
б) самопересекающуюся замкнутую;
в) простую
г) самопересекающуюся незамкнутую.
2. Определите число сторон простой ломаной, если она имеет:
а) 5 вершин;
б) 22 вершины.
3. Простая ломаная имеет:
а) 7 сторон;
б) 36 сторон.
Найдите количество ее вершин.
4. Какая имеется зависимость между числом вершин и сторон многоугольника?
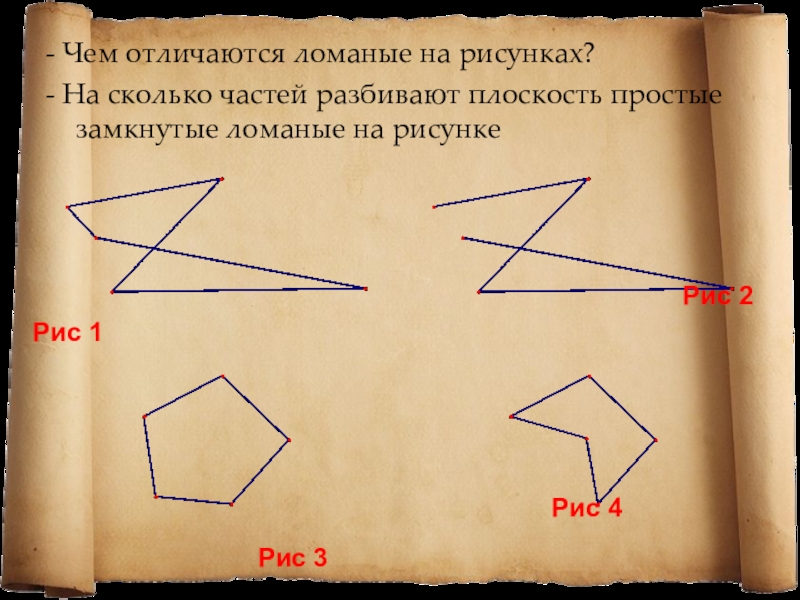
Слайд 5Рис 1
Рис 4
Рис 2
Рис 3
- Чем отличаются ломаные на рисунках?
- На
Слайд 6- Как назвать фигуру, состоящую из простой замкнутой ломаной и ограниченной
Многоугольник
Слайд 7Цель урока:
Приобрести знания и умения по теме «Многоугольники»
должны знать: определение
должны уметь: вычислять сумму углов многоугольника, количество диагоналей, градусную меру внутренних углов правильного многоугольника.
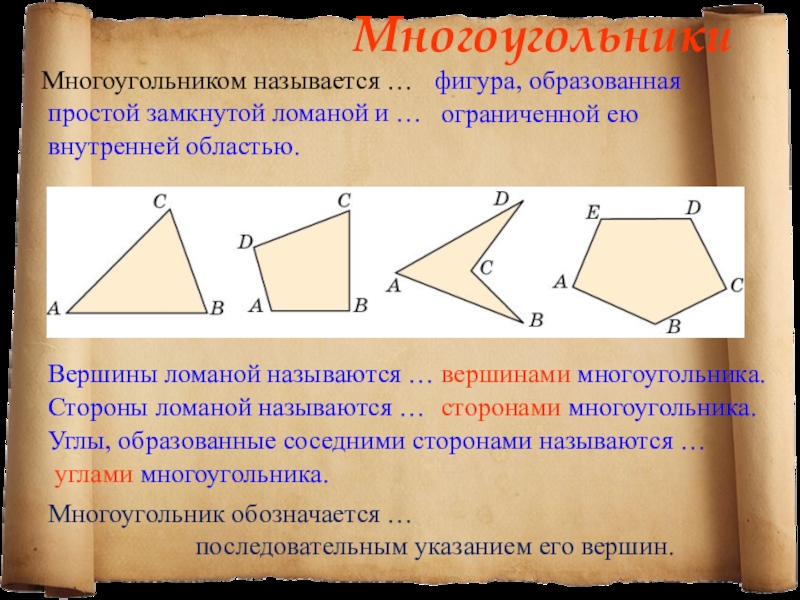
Слайд 8Многоугольники
Многоугольником называется …
вершинами многоугольника.
Вершины ломаной называются …
сторонами многоугольника.
Стороны ломаной называются …
углами многоугольника.
Углы, образованные соседними сторонами называются …
ограниченной ею внутренней областью.
последовательным указанием его вершин.
Многоугольник обозначается …
Слайд 9Выпуклые и невыпуклые многоугольники
Многоугольник называется выпуклым, если он лежит по одну
Многоугольник называется невыпуклым, если прямая, содержащая сторону многоугольника разбивает его на две части.
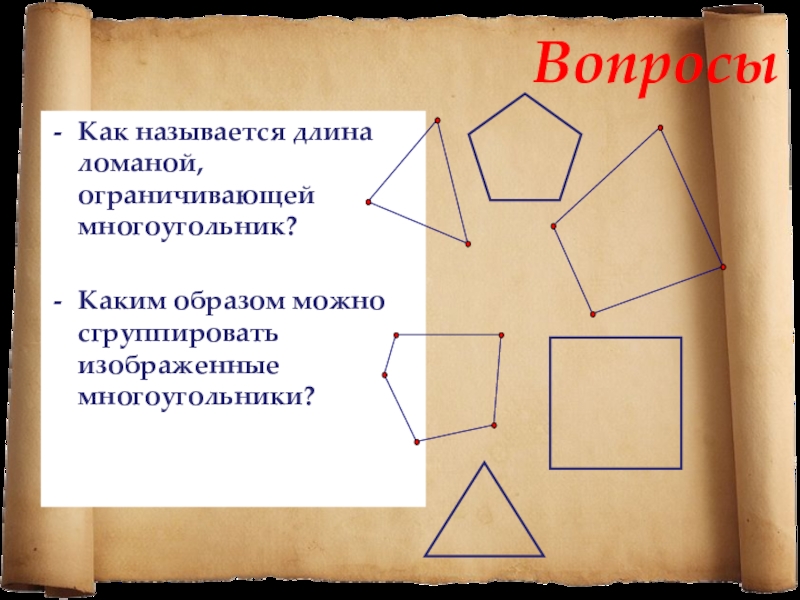
Слайд 10Вопросы
Как называется длина ломаной, ограничивающей многоугольник?
Каким образом можно сгруппировать изображенные многоугольники?
Слайд 11Правильные многоугольники
Представленные на рисунках многоугольники называют правильными. Почему?
Сформулируйте определение правильных многоугольников?
Слайд 14Великий математик, механик и инженер древности Архимед (греч.(греч. Αρχιμήδης, родился 287
Поскольку вычисление длины окружности считалось в древности весьма важной задачей, много усилий было затрачено на то, чтобы научиться оценивать периметр вписанной в нее правильного многоугольника при достаточно больших n. Особенно преуспел в этом Архимед.
Слайд 15Евклид ( родился в 330 году до н. э. в небольшом городке
Впрочем, правильные многоугольники привлекали внимание древнегреческих учёных задолго до Архимеда.
Пифагорейцы, в философии которых числа играли главную роль, придавали очень большое значение задаче о делении окружности на равные части, т. е. о построении правильного вписанного многоугольника.
В «Началах» Евклида приводятся построения с помощью циркуля и линейки правильных многоугольников с числом сторон от трёх до шести, а также пятнадцати угольника. «Начала» Евклида заканчиваются построением правильных многоугольников.
Задача о построение правильных многоугольников была полностью решена лишь спустя два тысячелетия.
Слайд 16
Знаменитый немецкий математик
К. Ф. Гаусс (1777- 1855) доказал следующую интересную
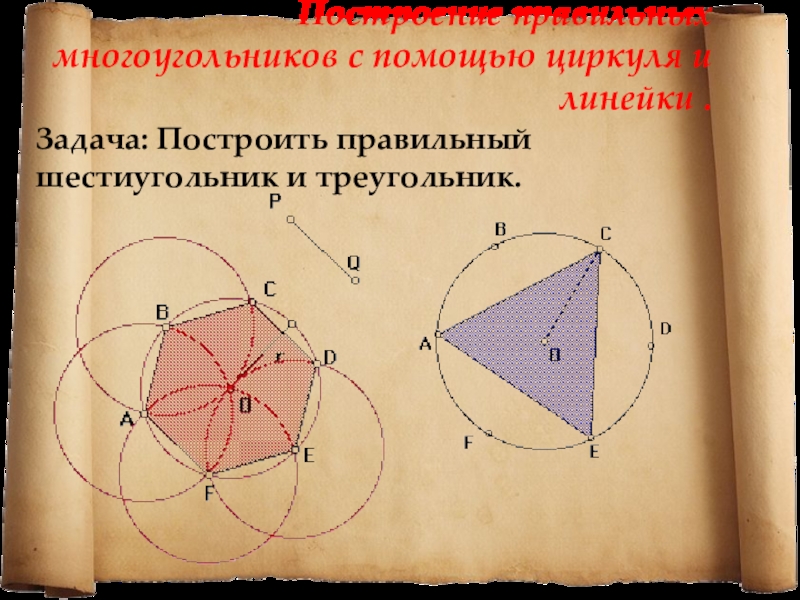
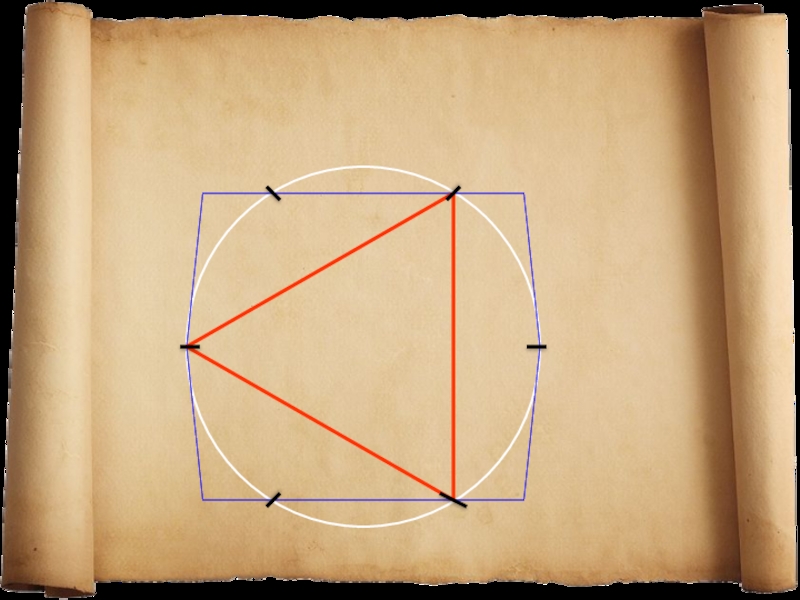
Слайд 19Построение правильных многоугольников с помощью циркуля и линейки .
Задача: Построить правильный
Слайд 21А так ли уж важно изучать и знать сведения о правильных
Историческая справка.
В математике паркетом называют «замощение» плоскости повторяющимися фигурами без пропусков и перекрытий. Простейшие паркеты были открыты пифагорейцами около 2500 лет тому назад.
Они установили, что вокруг одной точки могут лежать либо шесть правильных треугольников (), либо четыре квадрата (), либо три правильных шестиугольника (). Почему?
Слайд 22Пчелы – удивительные творения природы. Свои геометрические способности они проявляют при
Строя шестиугольные ячейки пчелы наиболее экономно используют площадь внутри небольшого улья и воск для изготовления ячеек.
Причем пчелиные соты представляют собой не плоский, а пространственный паркет, поскольку заполняют пространство так, что не остается просветов.
И как не согласиться с мнением пчелы из сказки «Тысяча и одна ночь»: «Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот».
Вы не задумывались над таким вопросом:
Почему пчелы «выбрали» себе для ячеек на сотах форму правильного шестиугольника?
Слайд 24Платоновы тела
Платоновы тела - трехмерный аналог плоских правильных многоугольников.
Существует лишь пять
Существование только пяти правильных многогранников относили к строению материи и Вселенной. Пифагорейцы, а затем Платон полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды
Согласно их мнению, атомы основных элементов должны иметь форму различных Платоновых тел.
Слайд 29Клуб исследователей по интересам
«Историки» - изучение истории вопроса
«Мыслители» - решение
«Исследователи природы» - изучение многоугольников, встречающихся в природе
«Практики» - применение многоугольников в наше время
«Программисты» - создание программы, позволяющей построить правильный многоугольник
сделай свой выбор!
Слайд 30Как мы будем работать
в проекте?
Работая в группах, мы:
Узнаем как можно
Будем использовать много разнообразных источников информации
Научимся решать типовые и практические задачи на построение
Попробуем себя в роли исследователей – выберем клуб по интересам
Представим результаты своей работы на конференции по завершению проекта
Слайд 34Домашнее задание
1) П.11
Группа А - № 195, № 200
Группа В
Группа С - №198, 201
2) Зарегистрироваться на gmail.com, отправить сообщение на адрес kler070674@gmail.com
3) Заполнить анкету участника проекта
4) Заполнить таблицу самозаписи участника проекта
Слайд 35Не закапывайте свой талант!
Помни!
1 из 1000 рождается гением,
1 из 100
1 из 10 000 000 становиться признанным Гением!