- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Многоугольники (8 класс)
Содержание
- 1. Презентация по геометрии на тему Многоугольники (8 класс)
- 2. Многоугольником называется фигура, составленная из отрезков АВ,
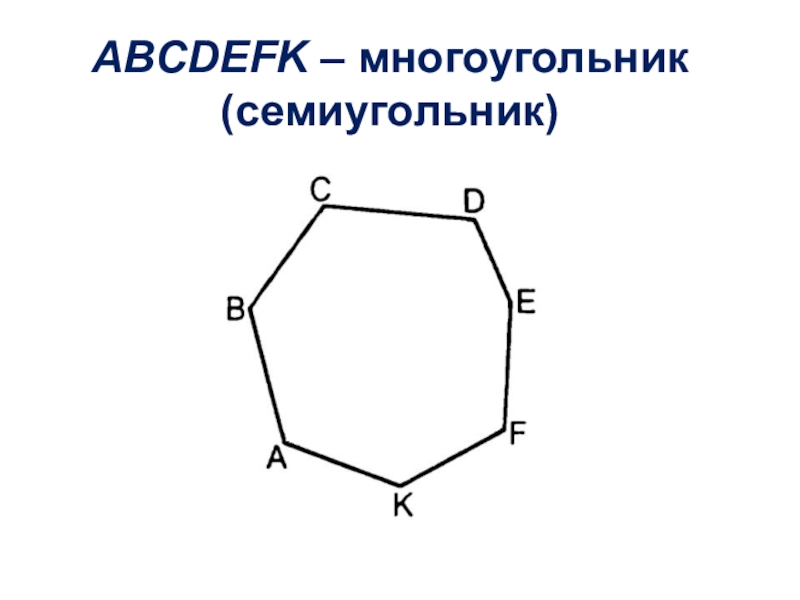
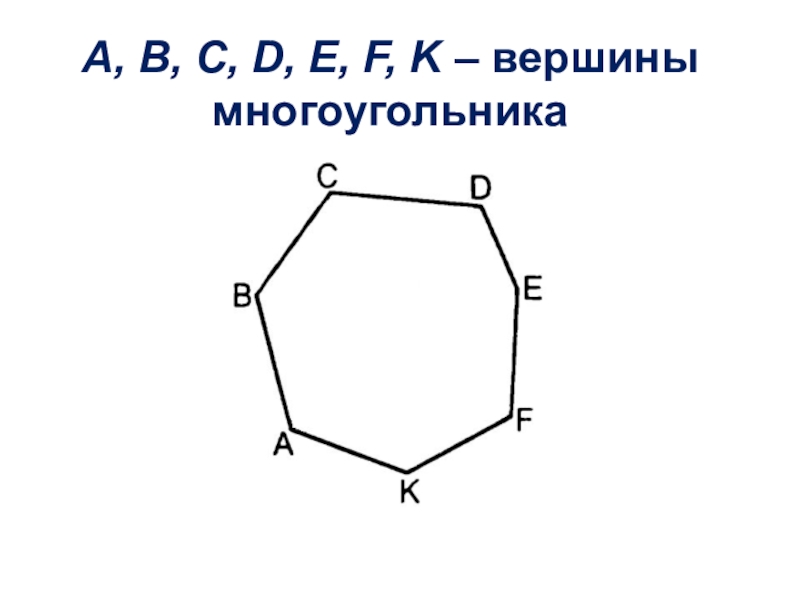
- 3. ABCDEFK – многоугольник (семиугольник)
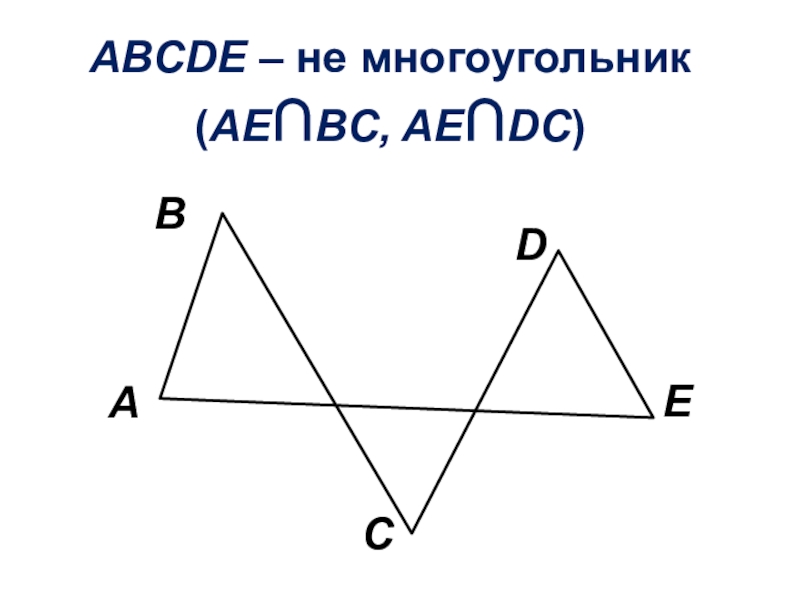
- 4. ABCDE – не многоугольник(AEBC, AEDC)ABCDE
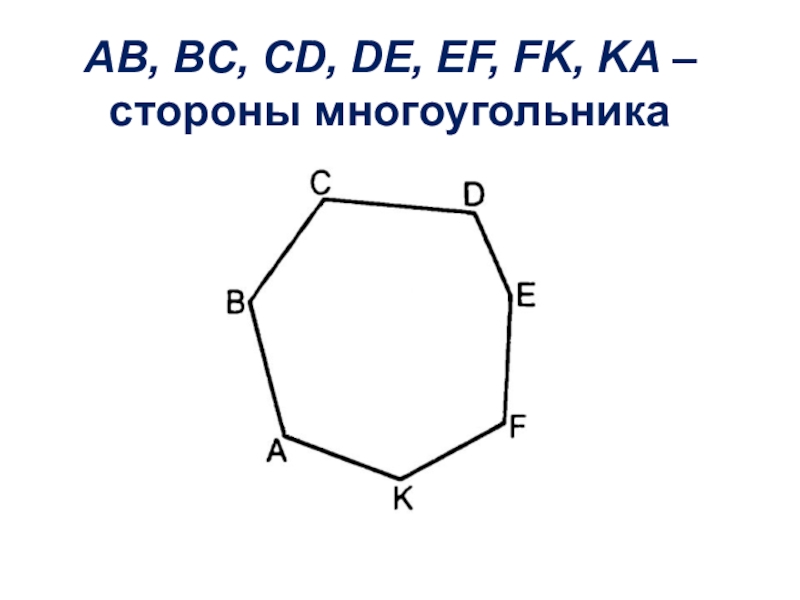
- 5. AB, BC, CD, DE, EF, FK, KA – стороны многоугольника
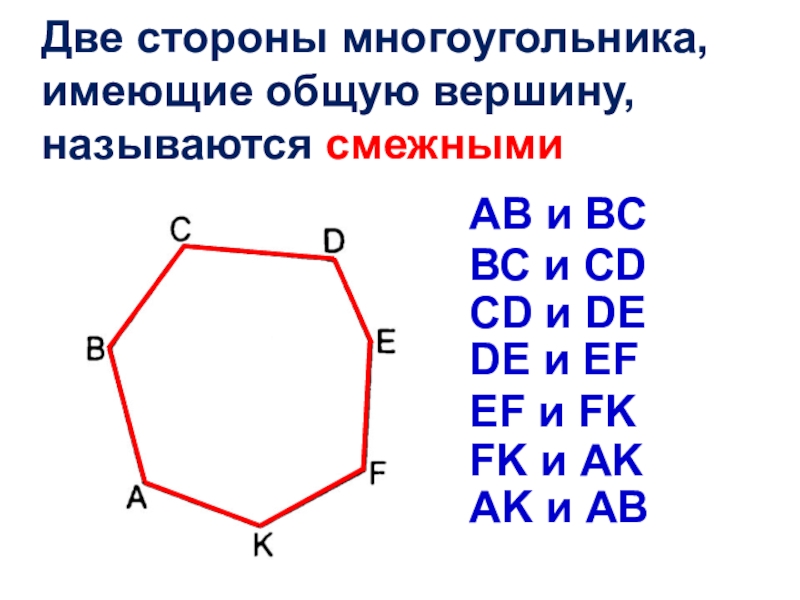
- 6. Две стороны многоугольника, имеющие общую вершину, называются
- 7. A, B, C, D, E, F, K – вершины многоугольника
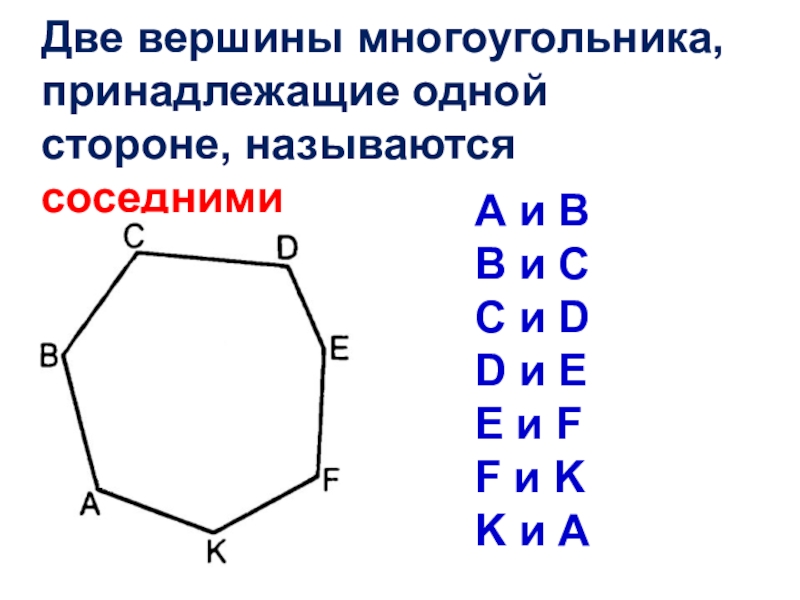
- 8. Две вершины многоугольника, принадлежащие одной стороне, называются
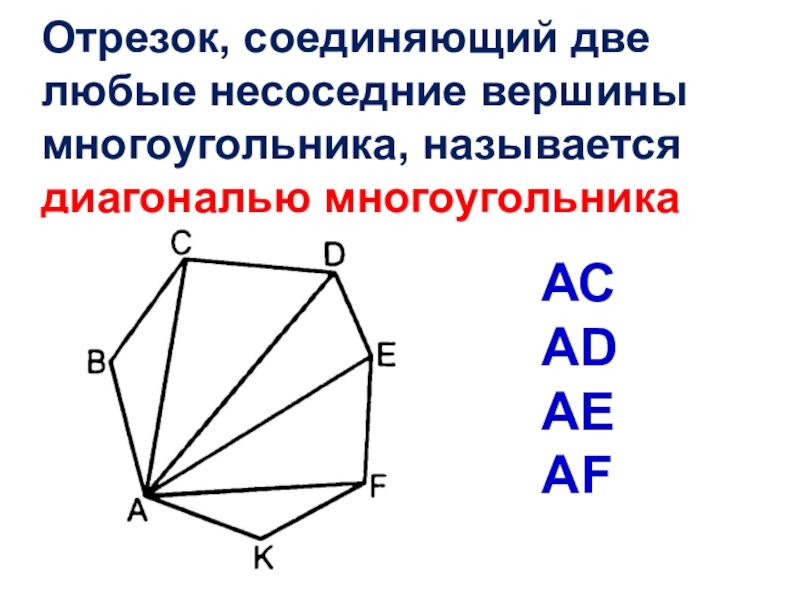
- 9. Отрезок, соединяющий две любые несоседние вершины многоугольника, называется диагональю многоугольникаАС АD АEАF
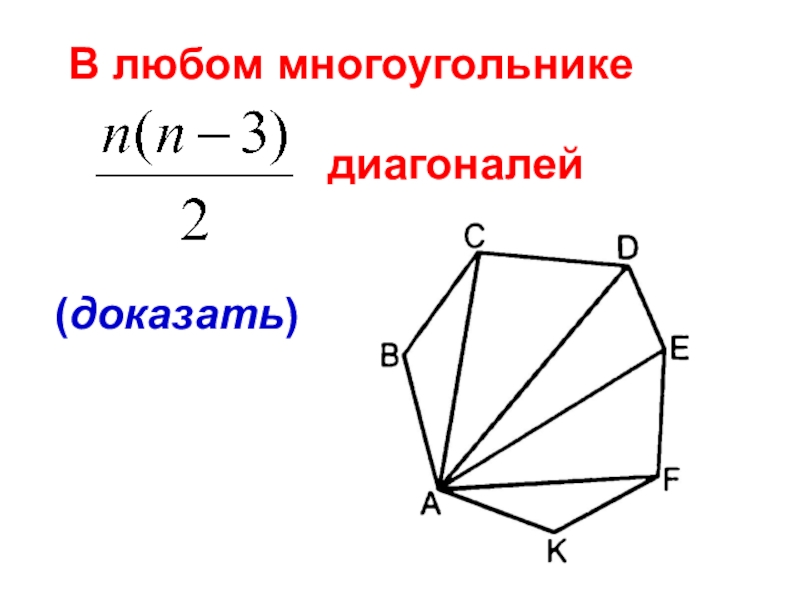
- 10. В любом многоугольнике диагоналей(доказать)
- 11. Периметром многоугольника называется сумма длин всех его
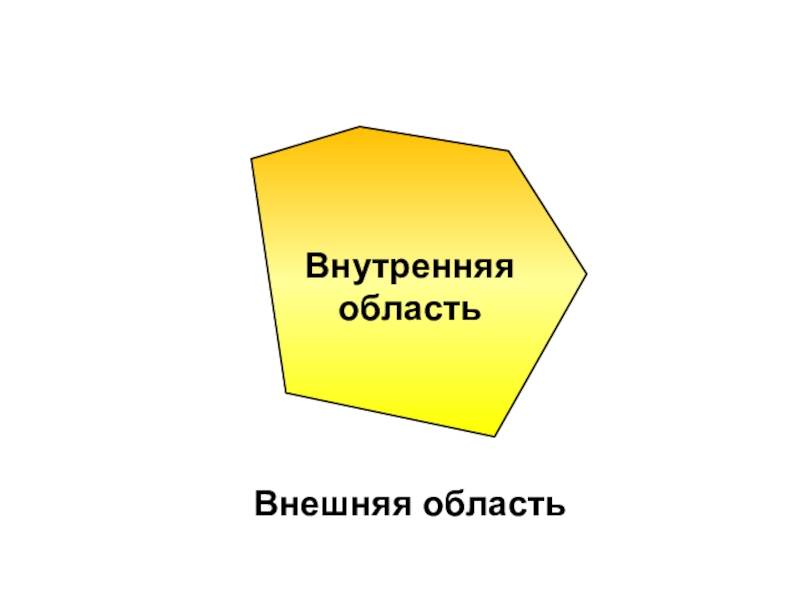
- 12. Внутренняя областьВнешняя область
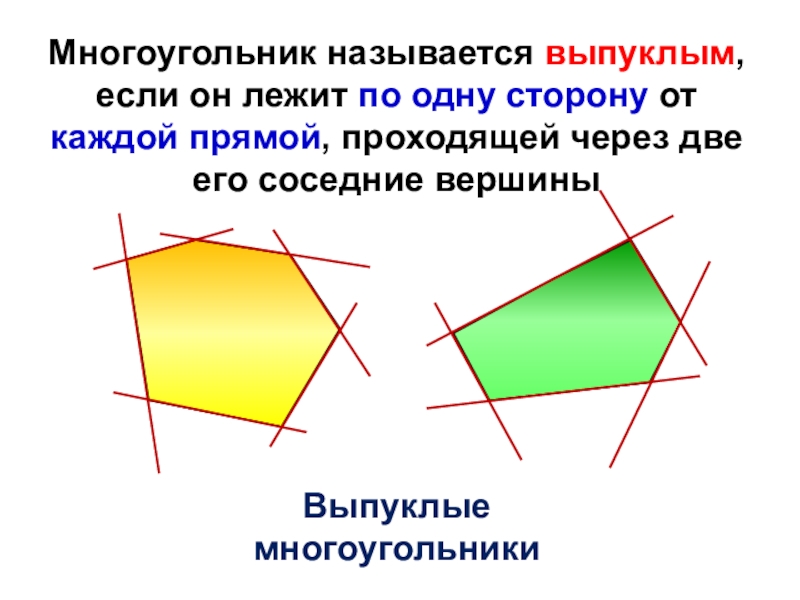
- 13. Выпуклые многоугольники Многоугольник называется выпуклым, если он
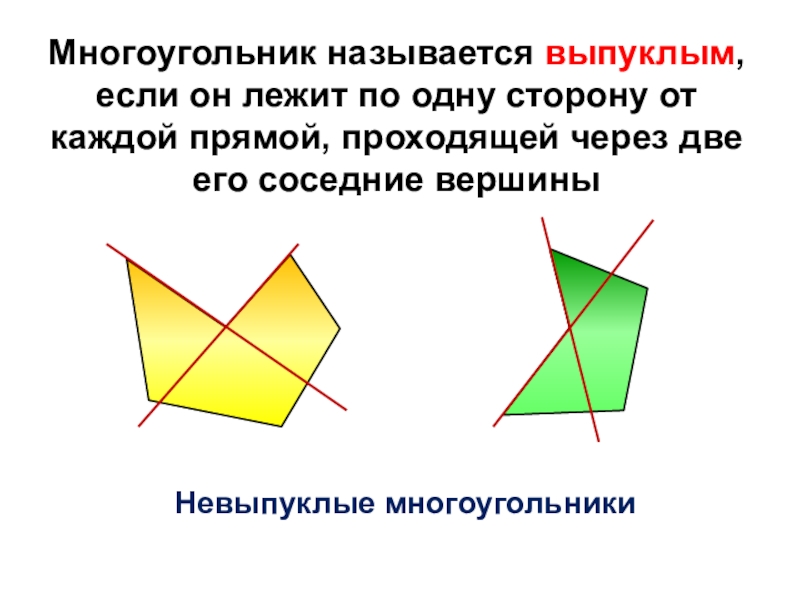
- 14. Невыпуклые многоугольники Многоугольник называется выпуклым, если он
- 15. Сумма углов выпуклого п – угольника равна (доказать)
- 16. Пример 1. Используя формулу для вычисления суммы
- 17. Пример 2. Найдите число сторон выпуклого многоугольника,
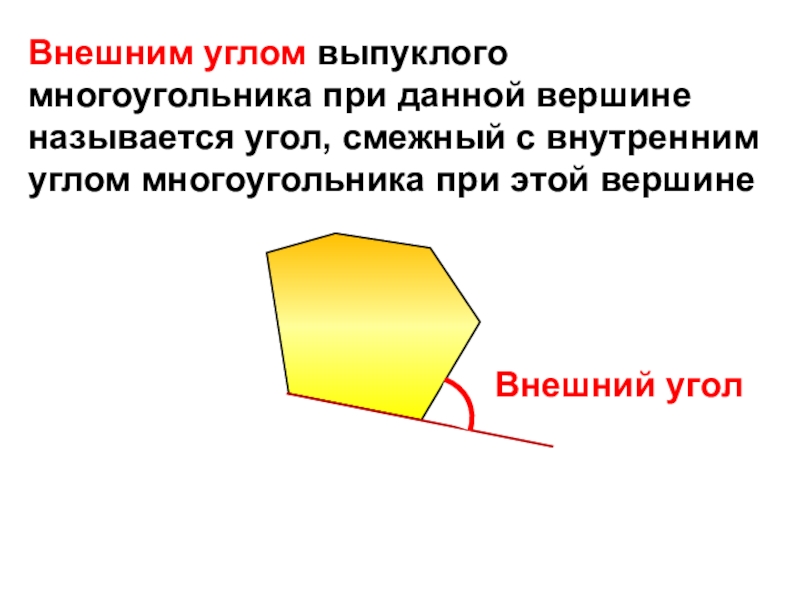
- 18. Внешний уголВнешним углом выпуклого многоугольника при данной
- 19. Сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине, равна 3600(доказать)
- 20. Четырёхугольники
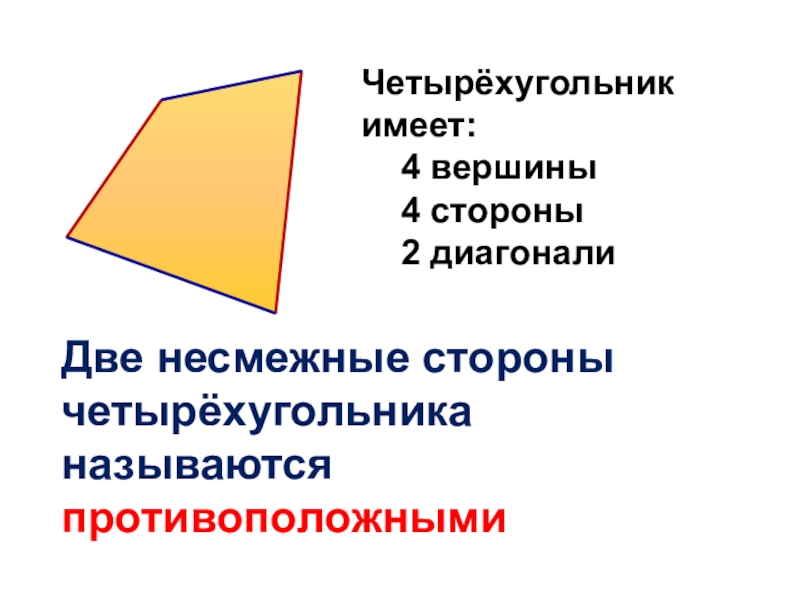
- 21. Две несмежные стороны четырёхугольника называются противоположнымиЧетырёхугольник имеет:4 вершины 4 стороны 2 диагонали
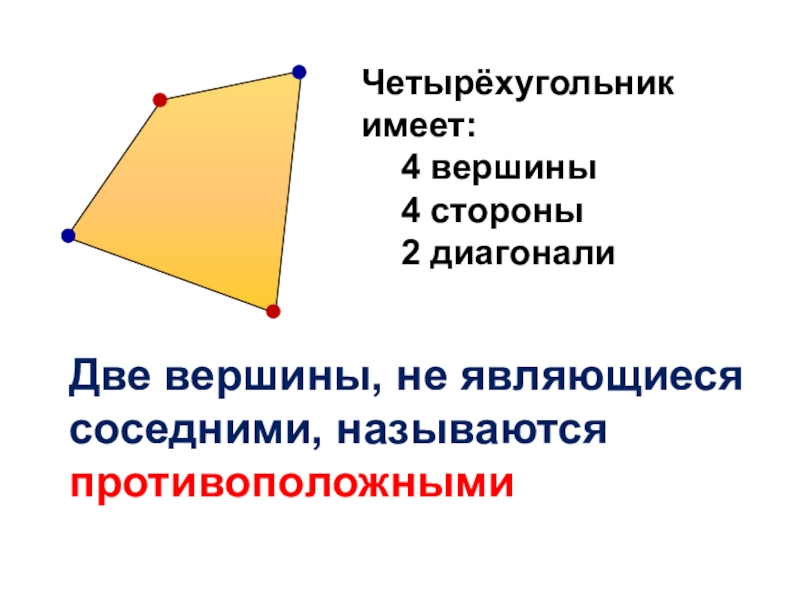
- 22. Две вершины, не являющиеся соседними, называются противоположнымиЧетырёхугольник имеет:4 вершины 4 стороны 2 диагонали
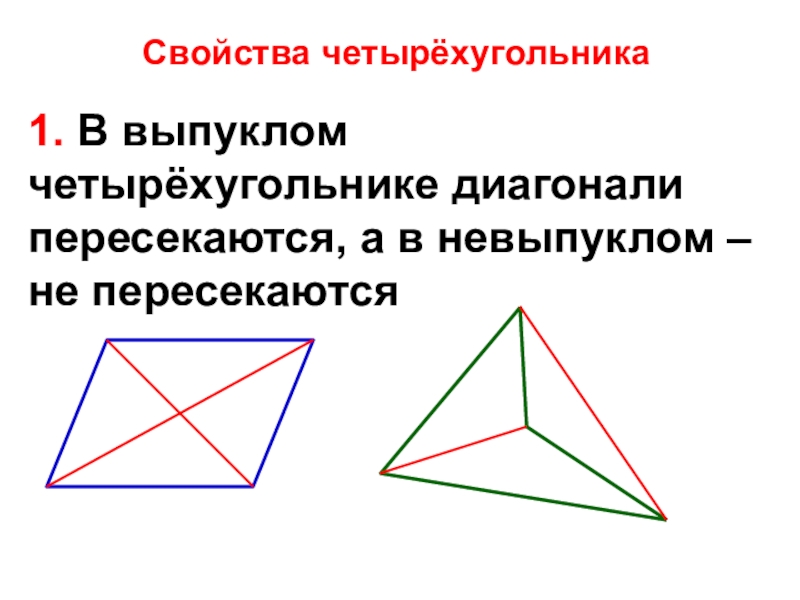
- 23. Свойства четырёхугольника1. В выпуклом четырёхугольнике диагонали пересекаются, а в невыпуклом – не пересекаются
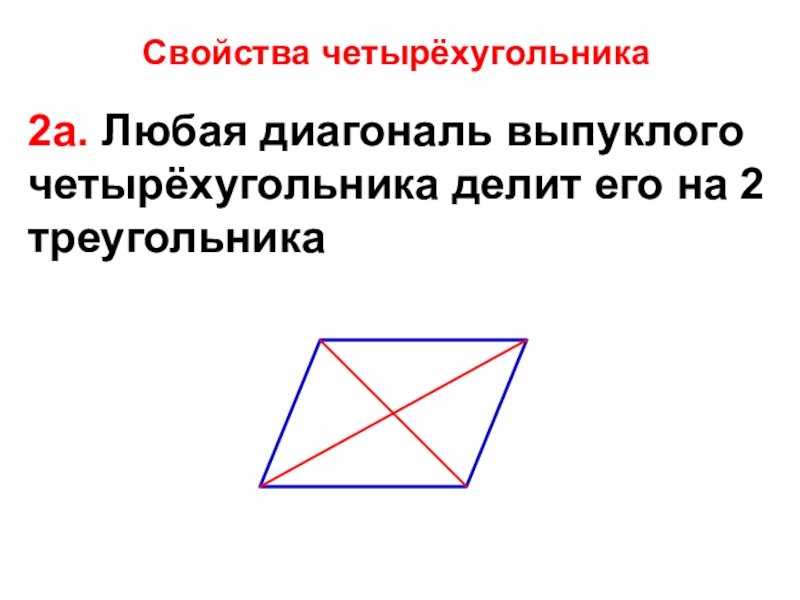
- 24. Свойства четырёхугольника2а. Любая диагональ выпуклого четырёхугольника делит его на 2 треугольника
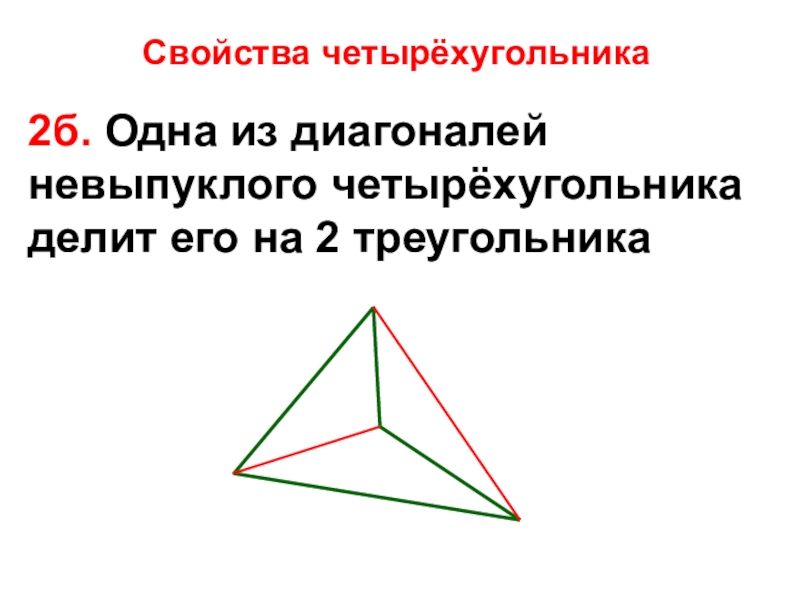
- 25. Свойства четырёхугольника2б. Одна из диагоналей невыпуклого четырёхугольника делит его на 2 треугольника
- 26. Свойства четырёхугольника3. Любой отрезок с концами на сторонах выпуклого четырёхугольника лежит во внутренней области этого четырёхугольника
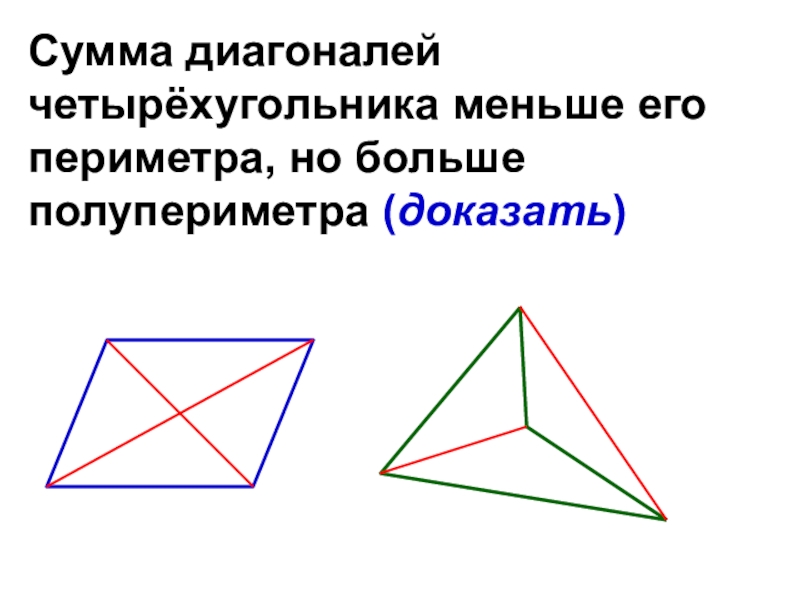
- 27. Сумма диагоналей четырёхугольника меньше его периметра, но больше полупериметра (доказать)
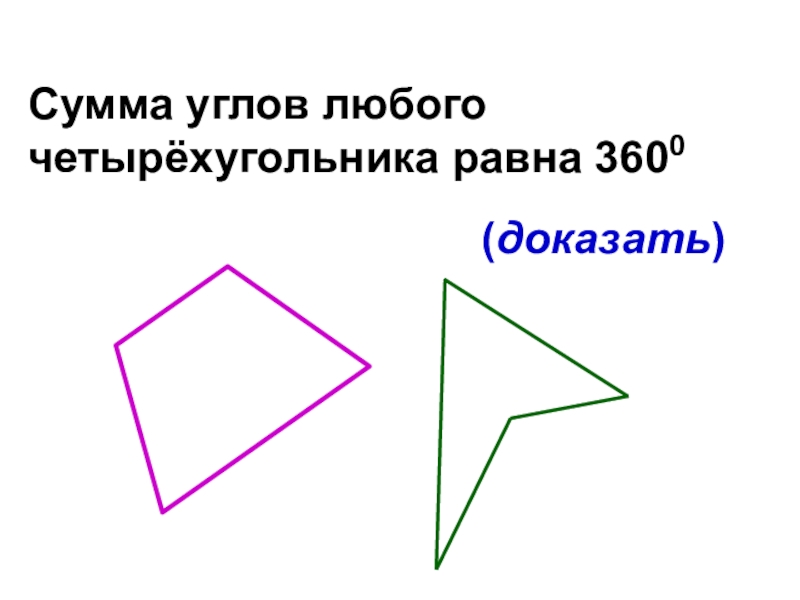
- 28. Сумма углов любого четырёхугольника равна 3600(доказать)
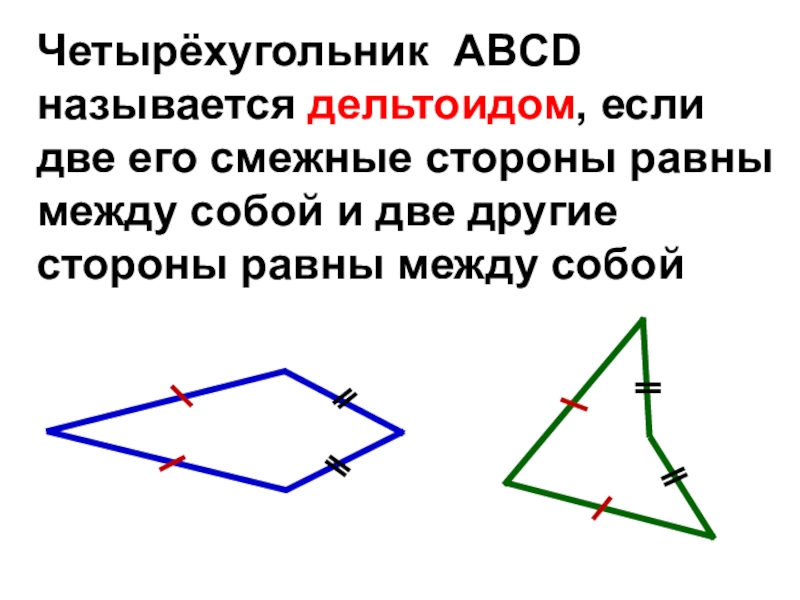
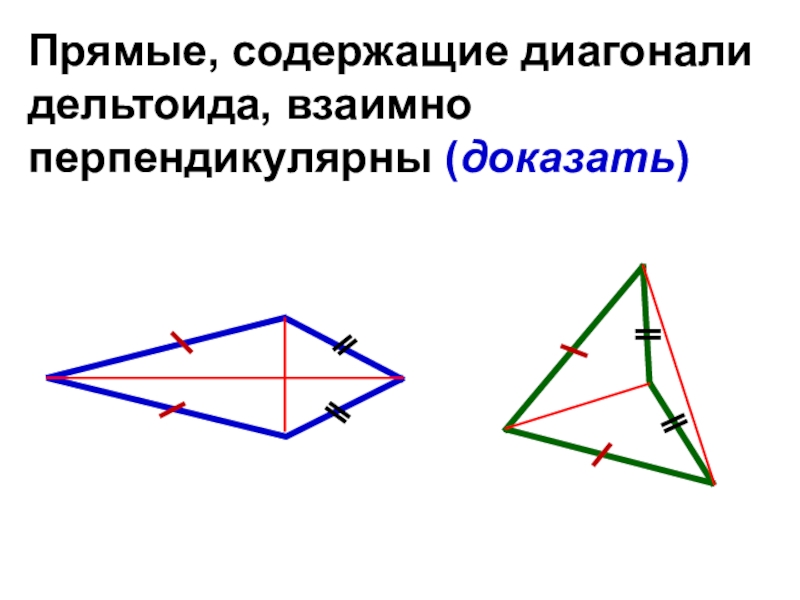
- 29. Четырёхугольник ABCD называется дельтоидом, если две его
- 30. Прямые, содержащие диагонали дельтоида, взаимно перпендикулярны (доказать)
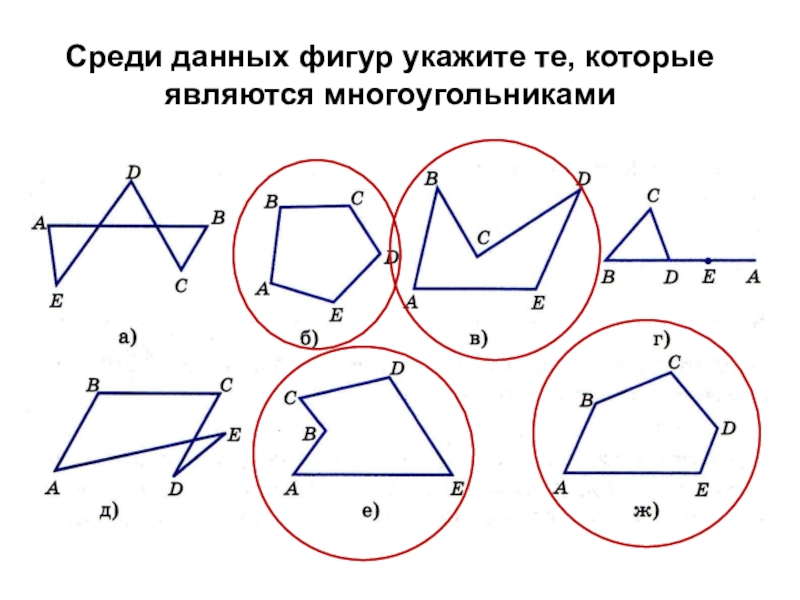
- 31. Среди данных фигур укажите те, которые являются многоугольниками
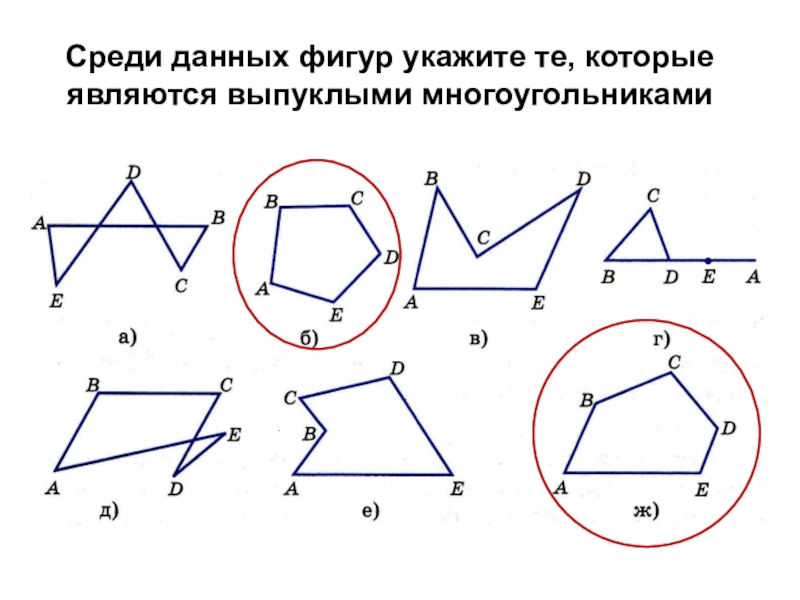
- 32. Среди данных фигур укажите те, которые являются выпуклыми многоугольниками
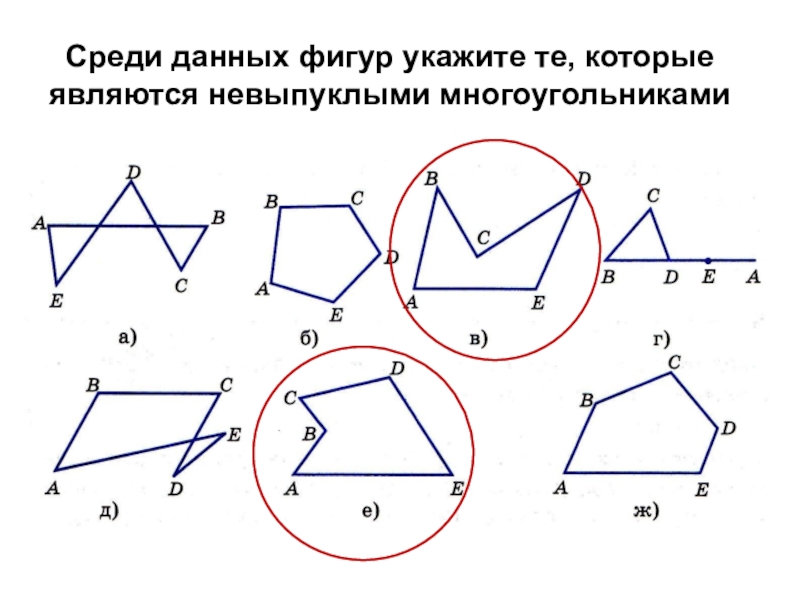
- 33. Среди данных фигур укажите те, которые являются невыпуклыми многоугольниками
- 34. Задание 1. Начертите в тетради 1 вариантВыпуклый пятиугольник ABCDE2 вариантВыпуклый шестиугольник ABCDEF
- 35. Запишите в тетради Вершины многоугольникаСтороны многоугольникаДиагонали многоугольникаВычислите сумму углов многоугольника
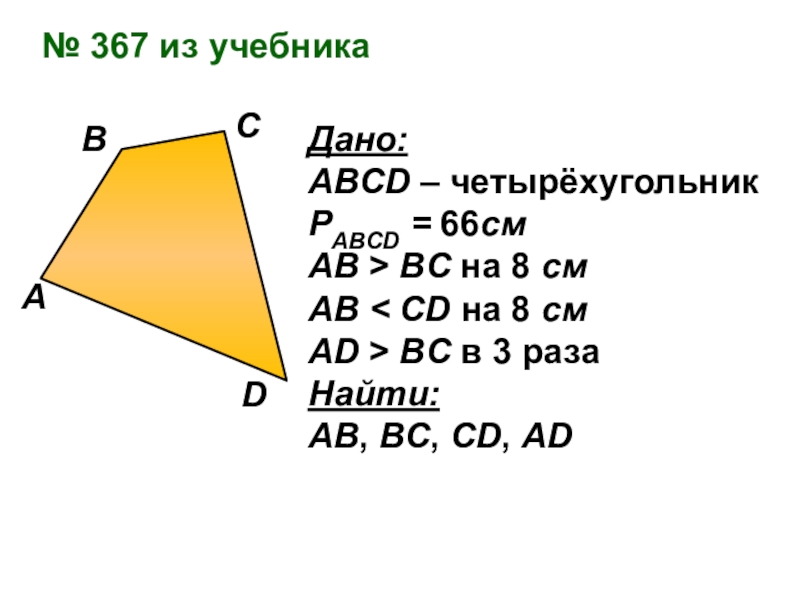
- 36. № 367 из учебникаДано: ABCD – четырёхугольникPABCD
- 37. Домашнее задание Пп. 39 – 41№ 364 № 365 № 366№ 368№ 369№ 370
- 38. Список литературыАтанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.
Многоугольником называется фигура, составленная из отрезков АВ, ВС, CD, DE, … так, что смежные отрезки (т.е. АВ и ВС, CD и DE…) не лежат на одной прямой, а несмежные отрезки не имеют общих точек
Слайд 2Многоугольником называется фигура, составленная из отрезков АВ, ВС, CD, DE, …
так, что смежные отрезки (т.е. АВ и ВС, CD и DE…) не лежат на одной прямой, а несмежные отрезки не имеют общих точек
Слайд 6Две стороны многоугольника, имеющие общую вершину, называются смежными
АВ и ВС
DЕ
и EF
CD и DE
ВС и CD
EF и FK
FK и AK
АK и АВ
Слайд 8Две вершины многоугольника, принадлежащие одной стороне, называются соседними
А и В
В
и C
C и D
D и E
E и F
F и K
K и А
C и D
D и E
E и F
F и K
K и А
Слайд 9Отрезок, соединяющий две любые несоседние вершины многоугольника, называется диагональю многоугольника
АС
АD
АE
АF
Слайд 11Периметром многоугольника называется сумма длин всех его сторон
РАВСDEFK = АВ +
ВС + CD + DE +
+ EF + FK + AK
+ EF + FK + AK
Слайд 13Выпуклые многоугольники
Многоугольник называется выпуклым, если он лежит по одну сторону
от каждой прямой, проходящей через две его соседние вершины
Слайд 14Невыпуклые многоугольники
Многоугольник называется выпуклым, если он лежит по одну сторону
от каждой прямой, проходящей через две его соседние вершины
Слайд 16Пример 1.
Используя формулу для вычисления суммы углов выпуклого многоугольника Sn
= 1800(n – 2), найдите сумму углов выпуклого:
а) одиннадцатиугольника
б) двадцатидвухугольника
S11 = 1800(11 – 2) = 18009 = 16200
S22 = 1800(22 – 2) = 180020 = 36000
Слайд 17Пример 2.
Найдите число сторон выпуклого многоугольника, каждый угол которого равен
1350.
Решение:
Сумма углов выпуклого n – угольника, каждый угол которого равен 1350, равна 1350 n; с другой стороны она равна 1800(n – 2)
1800(n – 2) = 1350 n
1800 n – 3600 = 1350 n
450 n = 3600
n = 8 Ответ: n = 8
Слайд 18Внешний угол
Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный
с внутренним углом многоугольника при этой вершине
Слайд 19Сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине,
равна 3600
(доказать)
Слайд 21Две несмежные стороны четырёхугольника называются противоположными
Четырёхугольник имеет:
4 вершины
4 стороны
2
диагонали
Слайд 22Две вершины, не являющиеся соседними, называются противоположными
Четырёхугольник имеет:
4 вершины
4 стороны
2 диагонали
Слайд 23Свойства четырёхугольника
1. В выпуклом четырёхугольнике диагонали пересекаются, а в невыпуклом –
не пересекаются
Слайд 24Свойства четырёхугольника
2а. Любая диагональ выпуклого четырёхугольника делит его на 2 треугольника
Слайд 25Свойства четырёхугольника
2б. Одна из диагоналей невыпуклого четырёхугольника делит его на 2
треугольника
Слайд 26Свойства четырёхугольника
3. Любой отрезок с концами на сторонах выпуклого четырёхугольника лежит
во внутренней области этого четырёхугольника
Слайд 29Четырёхугольник ABCD называется дельтоидом, если две его смежные стороны равны между
собой и две другие стороны равны между собой
Слайд 34Задание 1.
Начертите в тетради
1 вариант
Выпуклый пятиугольник ABCDE
2 вариант
Выпуклый шестиугольник
ABCDEF
Слайд 35Запишите в тетради
Вершины многоугольника
Стороны многоугольника
Диагонали многоугольника
Вычислите сумму углов многоугольника
Слайд 36№ 367 из учебника
Дано:
ABCD – четырёхугольник
PABCD = 66см
АВ > BC
на 8 см
АВ < CD на 8 см
AD > BC в 3 раза
Найти:
AB, BC, CD, AD
АВ < CD на 8 см
AD > BC в 3 раза
Найти:
AB, BC, CD, AD
Слайд 38Список литературы
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия: Учебник
для 7-9 кл. средней школы. Москва, 2014 г.
Гаврилова Н.Ф. Поурочные разработки по геометрии: 8 класс.– М.: ВАКО, 2010. (В помощь школьному учителю).
Гаврилова Н.Ф. Поурочные разработки по геометрии: 8 класс.– М.: ВАКО, 2010. (В помощь школьному учителю).
