- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Многогранники
Содержание
- 1. Презентация по геометрии на тему Многогранники
- 2. Определение: Многогранник – это часть пространства, ограниченная
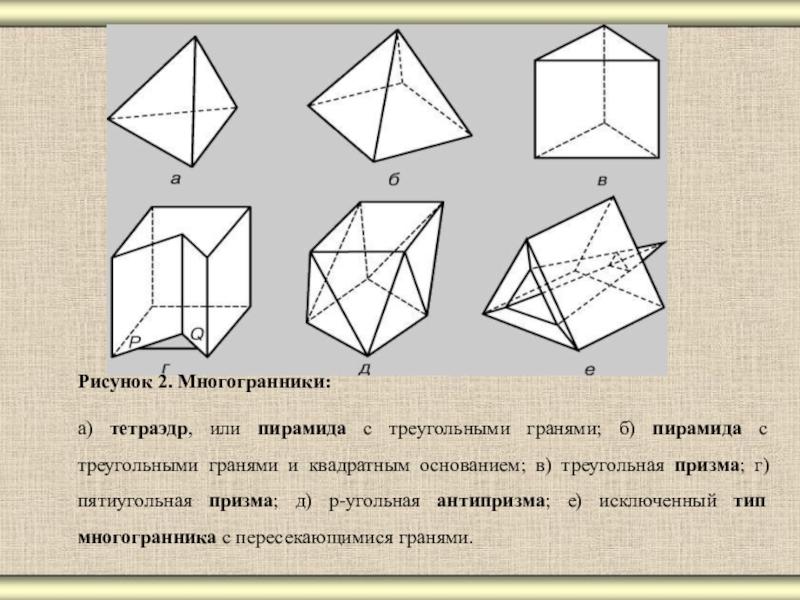
- 3. Рисунок 2. Многогранники: а) тетраэдр, или пирамида
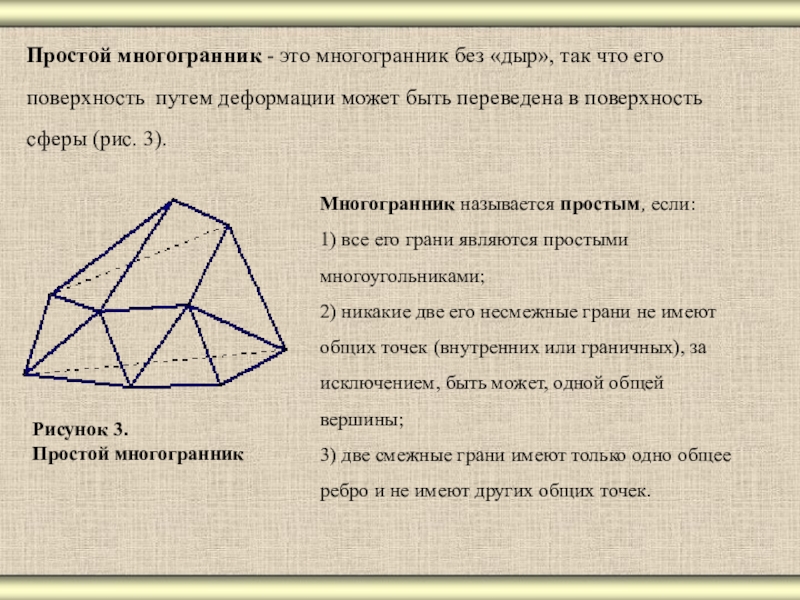
- 4. Простой многогранник - это многогранник без «дыр»,
- 5. Дело состоит в том, что при конструировании
- 6. Наглядно становится ясным, что простой многогранник можно
- 7. Теорема 1. Для всякого простого многогранника нулевого
- 8. Простой многогранник рода 1 можно получить из
- 9. Определение: Выпуклый многогранник называется топологически правильным, если
- 10. В самом деле, угол правильного n -
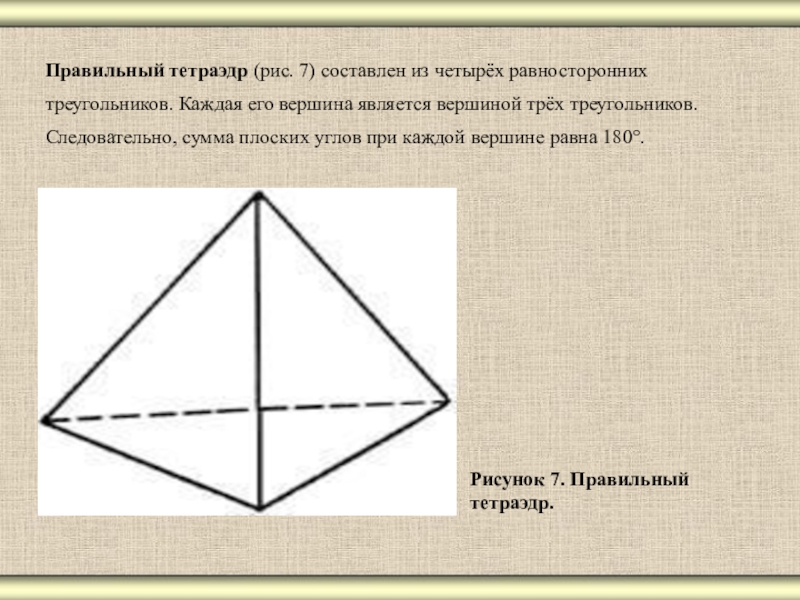
- 11. Правильный тетраэдр (рис. 7) составлен из четырёх
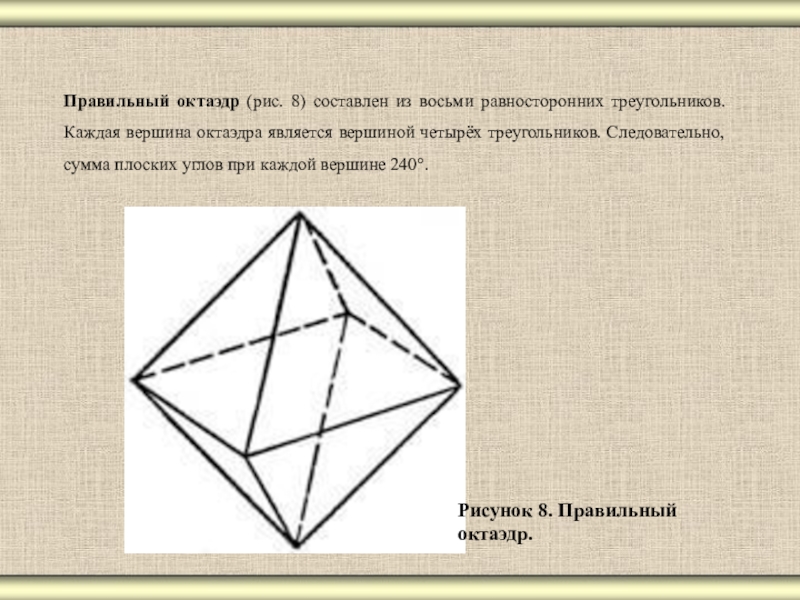
- 12. Правильный октаэдр (рис. 8) составлен из восьми
- 13. Правильный икосаэдр (рис. 9) составлен из двадцати
- 14. Куб (гексаэдр) (рис. 10) составлен из шести
- 15. Правильный додекаэдр (рис. 11) составлен из двенадцати
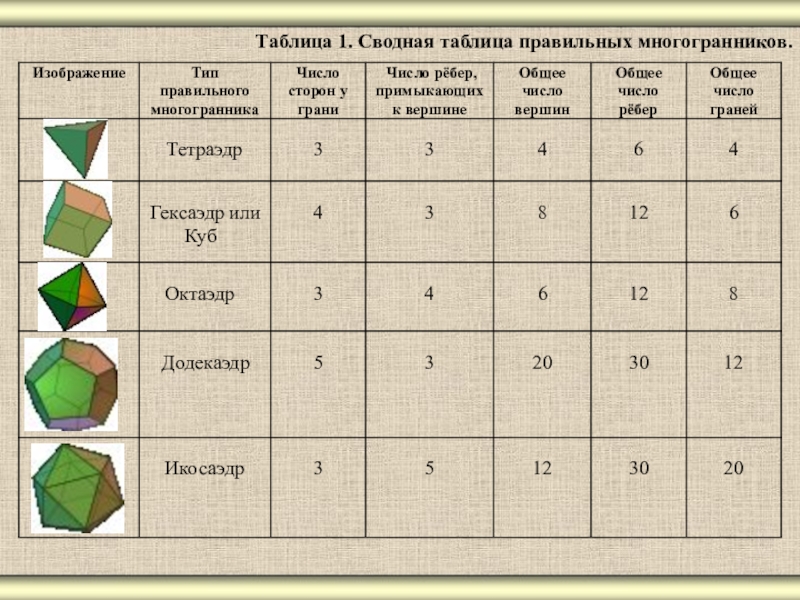
- 16. Таблица 1. Сводная таблица правильных многогранников.
- 17. Названия этих многогранников пришли из Древней Греции,
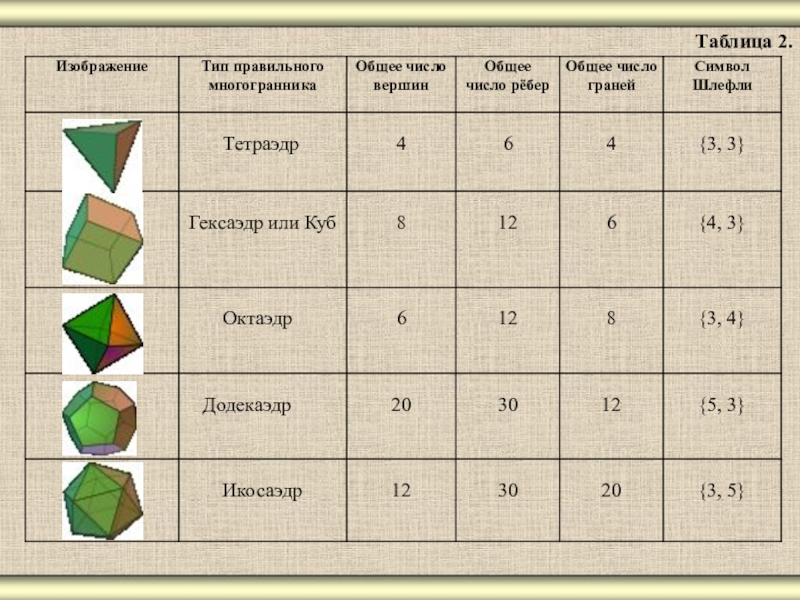
- 18. Таблица 2.
- 19. Работа Эйлера началась с
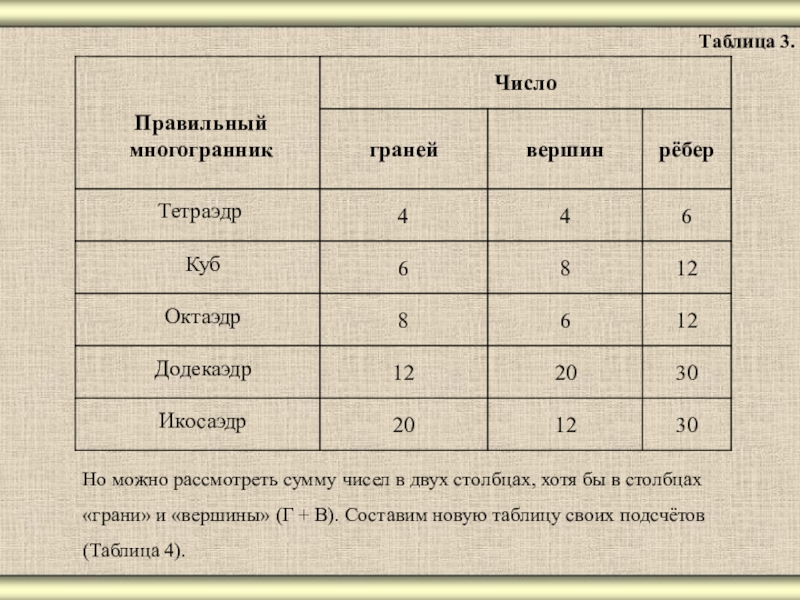
- 20. Таблица 3.Но можно рассмотреть сумму чисел в
- 21. Таблица 4.Вот теперь закономерности может не заметить
- 22. Задача 1. Для многогранника нулевого рода имеет
- 23. Решение. Каждому ребру можно
- 24. Задача 2. Докажите, что для любого простого
- 25. Решение. Из теоремы Эйлера имеем: 4В –
- 26. Задача 3. Докажите, что не существует многогранника,
- 27. Решение. Проведем доказательство методом
- 28. Задача 4. Докажите, что у любого многогранника число вершин, из которых выходит нечетное число ребер, четно.
- 29. Решение. Действительно, равенство 2Р
- 30. Задача 5. Докажите, что для всякого многогранника
- 31. Решение. а) Используя теорему
Слайд 2Определение: Многогранник – это часть пространства, ограниченная совокупностью конечного числа плоских
Многоугольники, из которых составлен многогранник, называются его гранями.
Стороны граней называются рёбрами, а концы рёбер – вершинами.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю.
Рисунок 1.
Слайд 3Рисунок 2. Многогранники:
а) тетраэдр, или пирамида с треугольными гранями; б)
Слайд 4Простой многогранник - это многогранник без «дыр», так что его
поверхность
сферы (рис. 3).
Многогранник называется простым, если:
1) все его грани являются простыми многоугольниками;
2) никакие две его несмежные грани не имеют общих точек (внутренних или граничных), за исключением, быть может, одной общей вершины;
3) две смежные грани имеют только одно общее ребро и не имеют других общих точек.
Рисунок 3.
Простой многогранник
Слайд 5Дело состоит в том, что при конструировании многогранника из тетраэдров для
Рисунок 4. Непростой многогранник «Картинная рама»
Слайд 6Наглядно становится ясным, что простой многогранник можно нужным нам образом составить
Рисунок 5. Разбиение на тетраэдры
Слайд 7Теорема 1. Для всякого простого многогранника нулевого рода
В - Р +
Всякий простой многогранник, не являющийся многогранником нулевого рода, имеет одну или несколько сквозных дыр. Число таких дыр называется родом многогранника. Многогранники рода 0, например, выпуклые многогранники. «Картинная рама» на рисунке 4 и многогранник на рисунке 6 — это простые многогранники рода 1.
Рисунок 6. Простой
многогранник рода 1
Слайд 8Простой многогранник рода 1 можно получить из двух простых многогранников рода
Теорема 2. Для всякого простого многогранника рода р справедливо соотношение
В - Р + Г = 2 - 2p.
Число 2 - 2р называют эйлеровой характеристикой многогранника.
Слайд 9Определение: Выпуклый многогранник называется топологически правильным, если его грани являются правильными
Всего существует пять видов топологически правильных выпуклых многогранников. Их гранями являются правильные треугольники, правильные четырёхугольники (квадраты) и правильные пятиугольники.
Докажем, что не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и, вообще, n – угольники при n ≥ 6.
Топологически правильные многогранники
Слайд 10В самом деле, угол правильного n - угольника при n ≥
По этой же причине каждая вершина топологически правильного многогранника может быть вершиной либо трёх, четырёх или пяти равносторонних треугольников, либо квадратов, либо трёх правильных пятиугольников. Других возможностей нет. В соответствии с этим получаем следующие топологически правильные многогранники, их всего 5.
Слайд 11Правильный тетраэдр (рис. 7) составлен из четырёх равносторонних треугольников. Каждая его
Рисунок 7. Правильный
тетраэдр.
Слайд 12Правильный октаэдр (рис. 8) составлен из восьми равносторонних треугольников. Каждая вершина
Рисунок 8. Правильный
октаэдр.
Слайд 13Правильный икосаэдр (рис. 9) составлен из двадцати равносторонних треугольников. Каждая вершина
Рисунок 9. Правильный
икосаэдр.
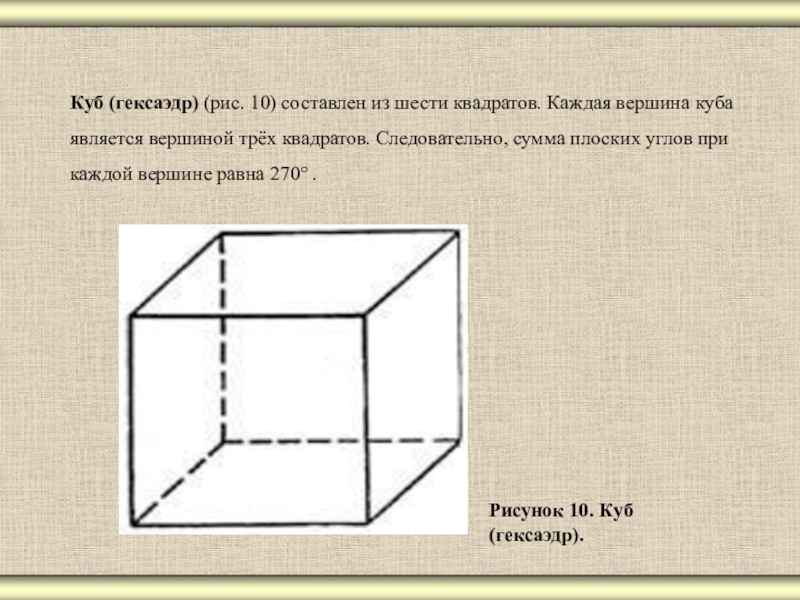
Слайд 14Куб (гексаэдр) (рис. 10) составлен из шести квадратов. Каждая вершина куба
Рисунок 10. Куб (гексаэдр).
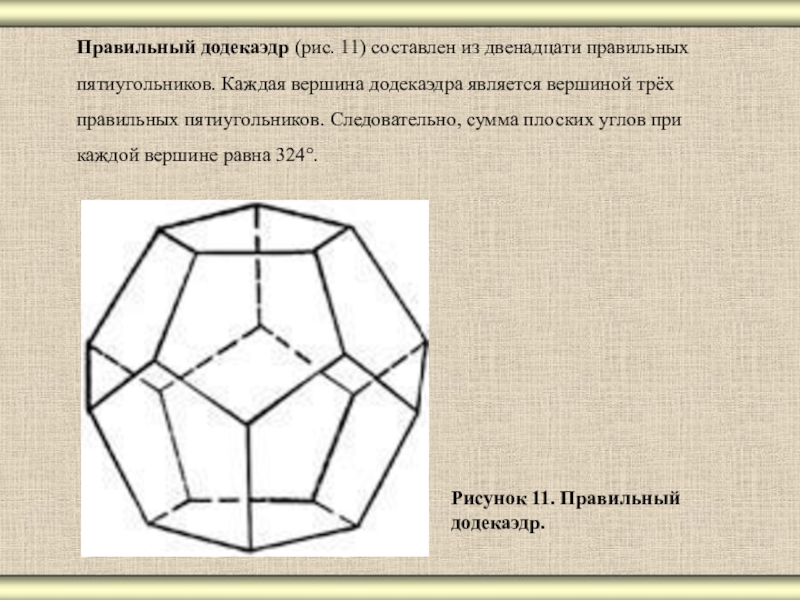
Слайд 15Правильный додекаэдр (рис. 11) составлен из двенадцати правильных пятиугольников. Каждая вершина
Рисунок 11. Правильный
додекаэдр.
Слайд 17Названия этих многогранников пришли из Древней Греции, и в них указывается
«эдра» - грань, «тетра» - 4, «гекса» - 6, «окта» - 8, «икоса» - 20, «додека» - 12.
Л.Шлефли (1814–1895), швейцарский математик которому принадлежит немало изящных результатов в геометрии и математическом анализе предложил обозначение {p, q}, где: p — число сторон каждой грани, q — число рёбер, сходящихся в каждой вершине.
Символы Шлефли для правильных многогранников приведены в таблице 2.
Слайд 19 Работа Эйлера началась с того, что он составил
Анализируя таблицу № 1, возникает вопрос: «Нет ли закономерности в возрастании чисел в каждом столбце?» По-видимому, нет. Например, в столбце «грани» казалось бы, просматривается закономерность (4 + 2 = 6, 6 + 2 = 8), но затем намеченная закономерность нарушается (8 + 2 ? 12, 12 + 2 ? 20). В столбце «вершины» нет даже стабильного возрастания.
Число вершин то возрастает (от 4 до 8, от 6 до 20), а то и убывает (от 8 до 6, от 20 до 12) . В столбце «рёбра» закономерности тоже не видно (Таблица 3).
«Формула Эйлера»
Слайд 20Таблица 3.
Но можно рассмотреть сумму чисел в двух столбцах, хотя бы
Слайд 21Таблица 4.
Вот теперь закономерности может не заметить только «слепой». Сформулируем её
Слайд 22Задача 1. Для многогранника
нулевого рода имеет место
равенство:
3Г3 +
Докажите.
Слайд 23 Решение. Каждому ребру можно сопоставить две вершины, соединенные
2Р = 3В3 + 4В4 + 5В5 + … .
С другой стороны, каждому ребру можно сопоставить две грани, прилегающие к нему. При этом n-угольная грань встречается n раз. Поэтому 2Р = 3Г3 + 4Г4 + 5Г5 + … ,
3Г3 + 4Г4 + 5Г5 + …= 3В3 + 4В4 + 5В5 + … .
Слайд 24Задача 2. Докажите, что для любого простого многогранника нулевого рода имеет
В3 + Г3 8
Слайд 25Решение. Из теоремы Эйлера имеем: 4В – 4Р + 4Г =
2Р = 3Г3 + 4Г4 + 5Г5 + … ,
2Р = 3В3 + 4В4 + 5В5 + … ,
В = В3 + В4 + В5 + … ,
Г = Г3 + Г4 + Г5 + … ,
получим:
4(В3 + В4 + В5 + … ) – (3В3 + 4В4 + 5В5 + …) – (3Г3 + 4Г4 + 5Г5 + …) + 4(Г3 + Г4 + Г5 + …) = 8,
откуда В3 + Г3 8.
Слайд 26Задача 3. Докажите, что не существует многогранника, каждая грань которого имеет
Слайд 27 Решение. Проведем доказательство методом от противного. Предположим, что
2Р = 3Г3 + 5Г5 + 7Г7 + … = (Г3 + Г5 + Г7 + …) + 2(Г3 + 2Г5 + 3Г7 + …).
Пришли к противоречию, так как Г3 + Г5 + Г7 – число нечетное, а 2(Г3 + 2Г5 + 3Г7 + …) – число четное, то их сумма должна быть нечетна, но 2Р – четное число.
Слайд 28Задача 4. Докажите, что у любого многогранника число вершин, из которых
Слайд 29 Решение. Действительно, равенство
2Р = 3В3 + 4В4
2Р = (В3 + В5 + В7 + …) + 2(В3 + 2В4 + 2В5 + …).
Откуда следует, что В3 + В5 + В7 – число четное.
Слайд 30Задача 5. Докажите, что для всякого многогранника нулевого рода имеют место
а) 6Г – 12 2Р и 3Г Р + 6
б) 6В – 12 2Р и 3В Р + 6.
Слайд 31 Решение. а) Используя теорему Эйлера, получим: 6В –
Докажем, что 2Р 3Г. Действительно, 2Р = 3Г3 + 4Г4 + 5Г5 + … 3Г3 + 3Г4 + 3Г5 + … = 3(Г3 + Г4 + Г5 + …) = 3Г. Итак, 2Р 3Г.
Наконец, докажем, что имеет место соотношение
3Г Р + 6. Действительно, 3В – 3Р + 3Г = 6, откуда 3Г = 3Р – 3В +6. Подставив 2Р 3В, получим 3Г Р + 6.
б) для любого многогранника 2Р = 3Г3 + 4Г4 + 5Г5 + … 3Г. С другой стороны, Г = Р – В + 2. Поэтому 2Р 3 (Р – В + 2), т.е. 3В Р + 6, 6В – 12 2Р.