- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Многогранники.
Содержание
- 1. Презентация по геометрии на тему Многогранники.
- 2. Из историиС древнейших времен наши представления о
- 3. Определения правильных многогранников.
- 4. Существует всего пять правильных многогранников: Тетраэдр, куб,
- 5. куб(гексаэдр)Куб (гексаэдр) - это правильный многогранник, у
- 6. Октаэдр Правильный октаэдр - правильный многогранник,
- 7. Икосаэдр Икосаэдр – это правильный многогранник, у
- 8. Додекаэдр Додекаэдр – это правильный
- 9. Некоторые свойства правильных многогранников.В выпуклом многограннике все
- 10. ТЕОРЕМА ЭЙЛЕРАЭйлерова характеристика всякого многогранника нулевого рода
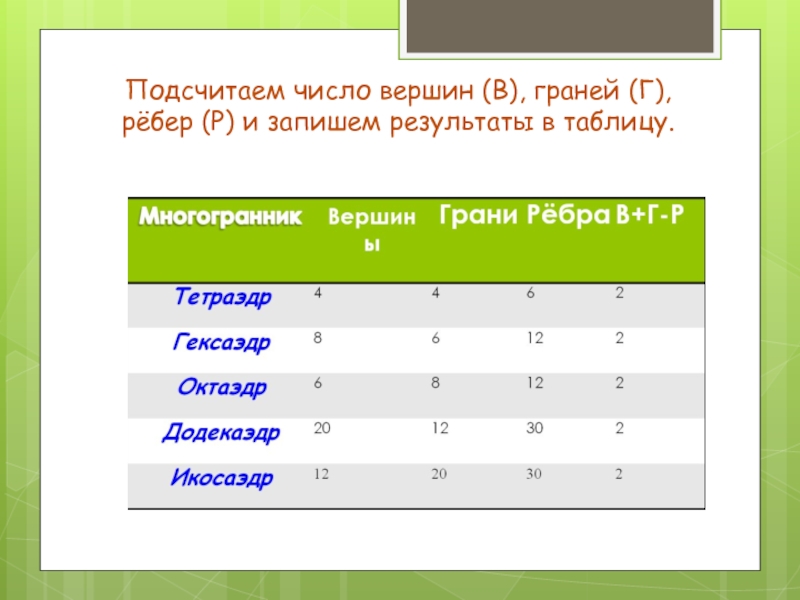
- 11. Подсчитаем
- 12. В последней колонке для всех многогранников один
- 13. Правильные многогранники можно встретить повсюдуПравильные многогранники в
- 14. Правильные многогранники в архитектуре Галикарнасский мавзолей, Храм Артемиды Эфесской, Башня Сююмбике, Мечеть Кул-Шариф, Башни Азриэли, Уникс, КГУ, Спасская башня Кремля.
- 15. Правильные многогранники искусстве Многогранники в живописи Титан
- 16. МАГИЯ «ИНЬ» И «ЯНЬ» В МНОГОГРАННИКАХСуществует концепция,
- 17. Слайд 17
- 18. Каждому геометрическому телу соответствует определённая стихия: куб
- 19. Слайд 19
- 20. Каждый минерал на Земле частично отражает структуру
Слайд 2Из истории
С древнейших времен наши представления о красоте связаны с симметрией.
Одно из древнейших упоминаний о правильных многогранниках находится в трактате Платона (427-347 до н. э.). Поэтому правильные многогранники также называются платоновыми телами. Каждый из правильных многогранников, а всего их пять, Платон ассоциировал с четырьмя земными элементами: земля (куб), вода (икосаэдр), огонь (тетраэдр), воздух (октаэдр), а также с неземным элементом - небом (додекаэдр).
Знаменитый математик и астроном Кеплер построил модель Солнечной системы как ряд последовательно вписанных и описанных правильных многогранников и сфер.
Слайд 3Определения правильных многогранников.
Имеется несколько эквивалентных определений правильных многогранников.
Одно из них звучит так: многогранник называется правильным, если существуют три концентрические сферы, одна из которых касается всех граней многогранника, другая касается всех его ребер и третья содержит все его вершины. Это определение напоминает одно из возможных определений правильного многоугольника: многоугольник называется правильным, если он вписан в некоторую окружность и описан около другой окружности, причем эти окружности концентричны.
Другое определение: правильным многогранником называется такой выпуклый многогранник, все грани которого являются одинаковыми правильными многоугольниками и все двугранные углы попарно равны.
Ещё одно определение правильных многогранников: многогранник называется правильным, если: он выпуклый все его грани являются равными правильными многоугольниками в каждой его вершине сходится одинаковое число граней все его двугранные углы равны.
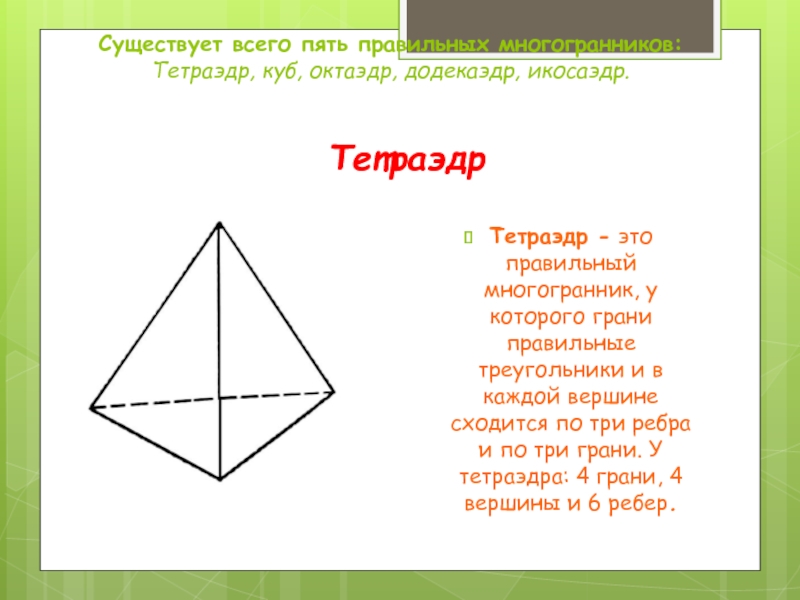
Слайд 4Существует всего пять правильных многогранников:
Тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
Тетраэдр
Тетраэдр - это
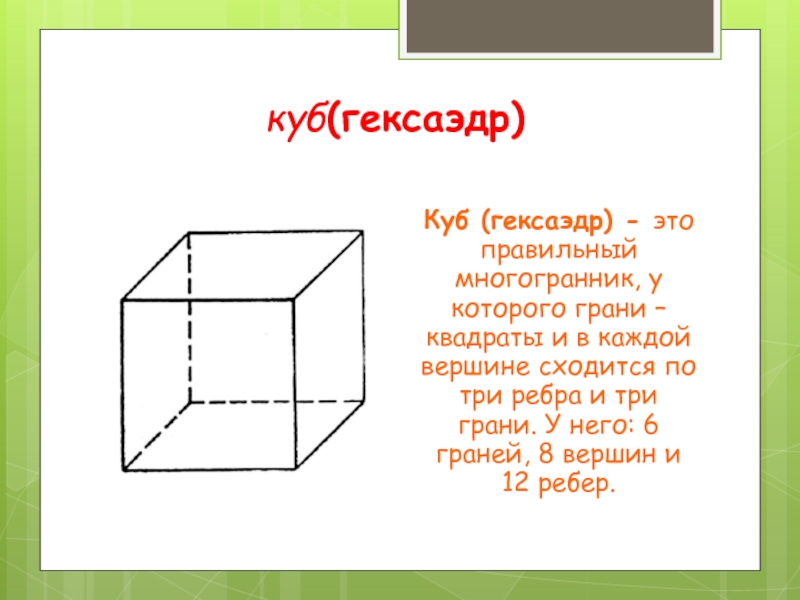
Слайд 5куб(гексаэдр)
Куб (гексаэдр) - это правильный многогранник, у которого грани – квадраты
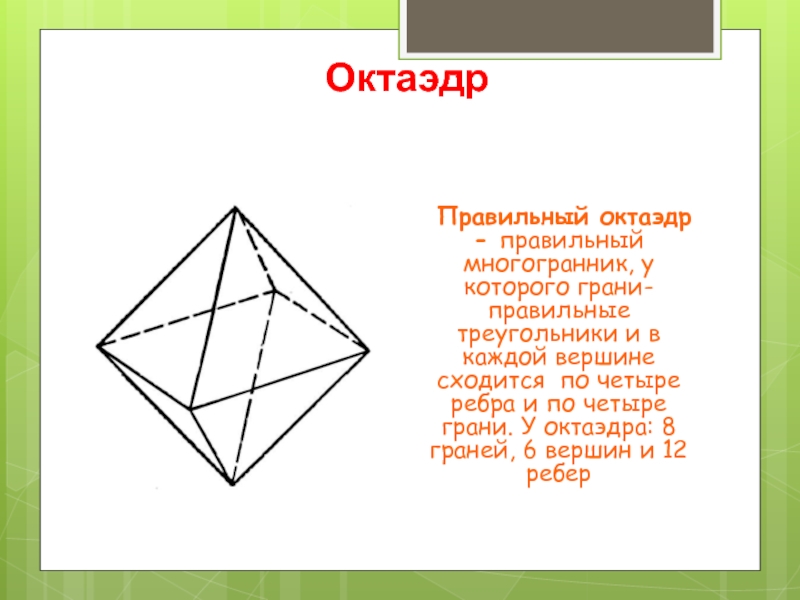
Слайд 6Октаэдр
Правильный октаэдр - правильный многогранник, у которого грани- правильные треугольники
Слайд 7Икосаэдр
Икосаэдр – это правильный многогранник, у которого грани правильные треугольники, но
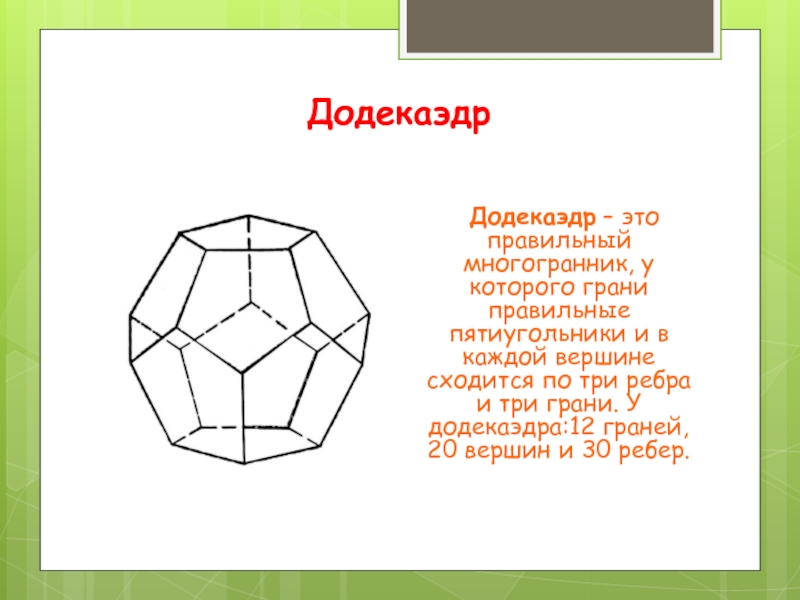
Слайд 8Додекаэдр
Додекаэдр – это правильный многогранник, у которого грани правильные
Слайд 9
Некоторые свойства правильных многогранников.
В выпуклом многограннике все грани – выпуклые многоугольники.
2.
3. Выпуклый многогранник лежит по одну сторону от плоскости каждой своей грани.
4. В 1752 году Леонард Эйлер доказал свойство, связывающее число его вершин, ребер и граней, получившее название теоремы Эйлера, справедливой для любого выпуклого многогранника.
Число вершин – число ребер + число граней = 2 (1)
5. Других видов правильных многогранников – нет.
6. Правильным многогранникам свойственна двойственность: если считать центры граней тетраэдра вершинами нового многогранника, то вновь получится тетраэдр; центры граней куба образуют октаэдр; центры граней октаэдра образуют куб; центры граней додекаэдра образуют икосаэдр; центры граней икосаэдра – додекаэдр.Кроме того, ребра правильного многогранника равны между собой и равны также все двугранные углы, содержащие две грани с общим ребром.
Слайд 10ТЕОРЕМА ЭЙЛЕРА
Эйлерова характеристика всякого
многогранника нулевого рода равна2.
Иначе говоря,
любого многогранника нулевого
рода имеет место зависимость .
Где е – число вершин,
f – число граней,
k – число ребер
e + f – k = 2
Слайд 12
В последней колонке для всех многогранников один и тот же результат:
Слайд 13Правильные многогранники можно встретить повсюду
Правильные многогранники в природе:
поваренная соль состоит
Слайд 14Правильные многогранники в архитектуре
Галикарнасский мавзолей, Храм Артемиды Эфесской, Башня Сююмбике, Мечеть Кул-Шариф, Башни Азриэли, Уникс,
Слайд 15Правильные многогранники искусстве
Многогранники в живописи Титан Возрождения, в работах Альбрехт Дюрер
Слайд 16МАГИЯ «ИНЬ» И «ЯНЬ» В МНОГОГРАННИКАХ
Существует концепция, что вершина многогранника отдает
Теперь применительно о концепции Инь-Янь к многогранникам. Рассмотрим соотношение вершин (энергия «Янь») и плоскостей (энергия «Инь») в пяти правильных многогранниках:
Слайд 18Каждому геометрическому телу соответствует определённая стихия: куб – Земля, икосаэдр –
Вторая их задача – направлять энергию Земли во время сдвига полюсов в особые точки планеты – на Северном и Южном полюсе. Пирамиды аккумулируют энергии, создавая энергоинформационные потоки, направленные в Космос, а также дают возможность получать информацию из Космоса.
Слайд 20
Каждый минерал на Земле частично отражает структуру Вселенной, и поэтому подчиняется
то есть в одном камне не в равной степени могут сосуществовать свойства всех четырех стихий. Цвет и огранка камня определенным образом ориентируют его свойства, выявляя скрытую, соответствующую планете или созвездию астральную энергию.
Вот почему жрецы и маги в древности держали в тайне формы огранки, соответствующие каждому виду минерала. Древнегреческий философ Гераклит заметил, что «скрытая гармония сильнее явной». Перед покупкой драгоценного камня необходимо хорошо оценить его огранку, ведь именно она влияет на способ проявления энергии самоцвета.
Иногда минералы винят в их способности приносить несчастья, их даже называют проклятыми. Но, на самом деле, самоцветы не в чем винить, так как они являются прямым отражением поступков своих владельцев. Они лишь перерабатывают информацию и энергию, обращая ее либо в позитив, либо в негатив.
Поэтому не следует пускать все на самотек, быть безжалостным и эгоистичным. Необходимо делать жертвы во имя достижения цели, и если Вы готовы пойти на это, то камни в бриллиантовой огранке всегда помогут достичь успеха. В противном же случае, если Вы не хотите работать над собой, развиваться и получать пользу от своих поступков, то самоцветы будут приносить в Вашу жизнь лишь негатив.