- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Методы построения сечений в многогранниках
Содержание
- 1. Презентация по геометрии на тему Методы построения сечений в многогранниках
- 2. МЕТОДЫ ПОСТРОЕНИЯ СЕЧЕНИЙИспользование свойств параллельных прямых и плоскостейМетод следовМетод внутреннего проектирования
- 3. КомментарийВ задачах на построение в стереометрии удобно
- 4. Использование свойств параллельных прямых и плоскостейЗадача 1.
- 5. ТКИспользование свойств параллельных прямых и плоскостейЗадача 1.
- 6. Использование свойств параллельных прямых и плоскостейЗадача 1.
- 7. Использование свойств параллельных прямых и плоскостейЗадача 2.
- 8. Использование свойств параллельных прямых и плоскостейЗадача 2.
- 9. Метод следовСодержание методаСначала строят прямую пересечения секущей
- 10. Метод следовНеобходимо помнить, что точка пересечения какой-либо
- 11. Метод следовЕсли рассматривать параллельное (или центральное) проектирование,
- 12. Задача 3. Постройте сечение куба ABCDA1B1C1D1 плоскостью,
- 13. Задача 3. Постройте сечение куба ABCDA1B1C1D1 плоскостью,
- 14. Задача 3. Постройте сечение куба ABCDA1B1C1D1 плоскостью,
- 15. Задача 3. Постройте сечение куба ABCDA1B1C1D1 плоскостью,
- 16. Метод внутреннего проектированияСодержание методаИмея три точки, которые
- 17. Метод внутреннего проектированияЗадача 3. Постройте сечение куба
- 18. Метод внутреннего проектированияЗадача 3. Постройте сечение куба
- 19. Метод внутреннего проектированияЗадача 3. Постройте сечение куба
- 20. Метод внутреннего проектированияЗадача 3. Постройте сечение
- 21. Применение методов построения сечений многогранников при решении
- 22. Применение методов построения сечений многогранников при решении
- 23. Применение методов построения сечений многогранников при решении
- 24. Применение методов построения сечений многогранников при решении
- 25. Применение методов построения сечений многогранников при решении
- 26. Применение методов построения сечений многогранников при решении
- 27. Применение методов построения сечений многогранников при решении
- 28. Применение методов построения сечений многогранников при решении
- 29. Источники информацииНелин Е.П. Комплексная подготовка к ЕГЭ
Слайд 1РЕШЕНИЕ ЗАДАЧ
НА ПОСТРОЕНИЕ СЕЧЕНИЙ
В МНОГОГРАННИКАХ
Разработка
учителя математики
Макиной Л.Н.
Слайд 2МЕТОДЫ ПОСТРОЕНИЯ СЕЧЕНИЙ
Использование свойств параллельных прямых и плоскостей
Метод следов
Метод внутреннего проектирования
Слайд 3Комментарий
В задачах на построение в стереометрии удобно использовать схему решения задач
На этапе анализа предполагаем, что задача уже решена, выполняем соответствующий рисунок и, опираясь на известные свойства прямых и плоскостей, пробуем составить план построения.
На этапе построения по составленному плану описываем построение, детализируя его до элементарных построений в изображённых плоскостях.
На этапе доказательства обосновываем, что в результате построения действительно получили фигуру с заданными свойствами.
На этапе исследования рассматриваем каждый шаг построения и отвечаем на два вопроса: 1) Всегда ли можно выполнить этот шаг? 2) Сколько фигур получим в результате?
Слайд 4Использование свойств параллельных прямых и плоскостей
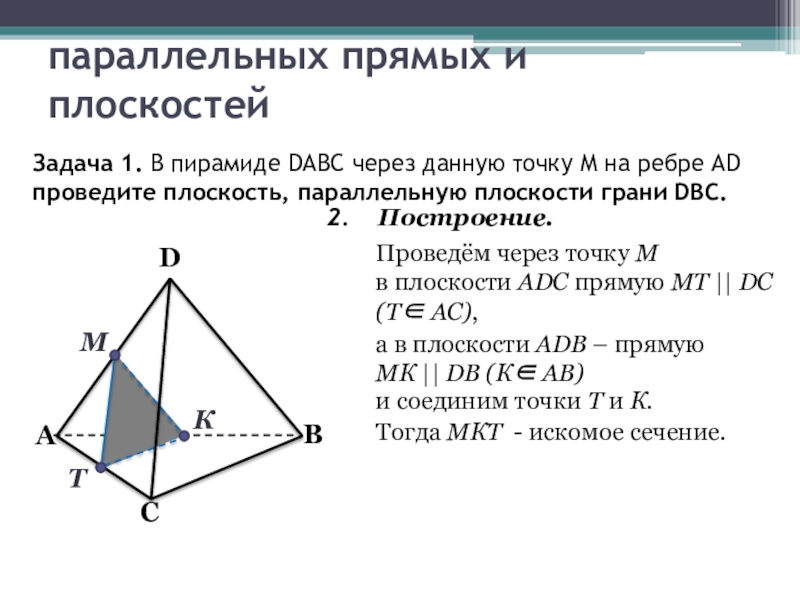
Задача 1. В пирамиде DABC через
Анализ.
Допустим, что задача решена и соответствующее сечение МКТ построено.
Т.к. (МКТ) || (DBC), то грани ADC, ADB и АВС пересекают параллельные плоскости по параллельным прямым.
Значит, МК || DB, МТ || DC и
ТК || ВС.
Это даёт возможность выполнить построение.
М
Слайд 5Т
К
Использование свойств параллельных прямых и плоскостей
Задача 1. В пирамиде DABC через
Проведём через точку М
в плоскости ADC прямую МТ || DC (Т АС),
М
В
А
С
D
а в плоскости ADB – прямую
МК || DB (К АВ)
и соединим точки Т и К.
Тогда МКТ - искомое сечение.
Построение.
Слайд 6Использование свойств параллельных прямых и плоскостей
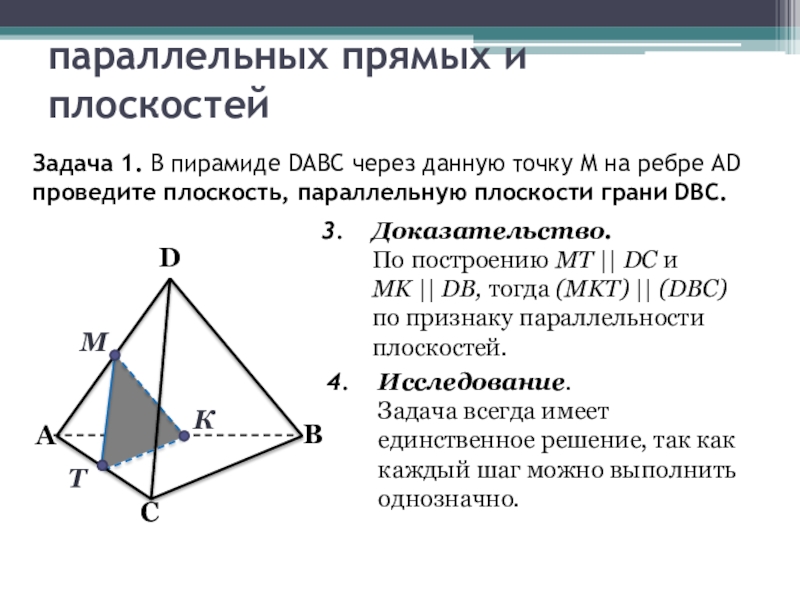
Задача 1. В пирамиде DABC через
Доказательство.
По построению МТ || DC и
MK || DB, тогда (MKT) || (DBC) по признаку параллельности плоскостей.
Исследование.
Задача всегда имеет единственное решение, так как каждый шаг можно выполнить однозначно.
М
Слайд 7Использование свойств параллельных прямых и плоскостей
Задача 2. Постройте сечение прямоугольного параллелепипеда
Ориентир.
Если данный многогранник содержит параллельные грани, которые пересекает плоскость сечения, то линии пересечения секущей плоскости с этими гранями параллельны.
/Свойство параллельного проектирования/
N
М
К
Слайд 8Использование свойств параллельных прямых и плоскостей
Задача 2. Постройте сечение прямоугольного параллелепипеда
Точки М и N принадлежат секущей плоскости и лежат в одной грани АВВ1А1, поэтому их можно соединить отрезком MN.
N
М
К
Т.к. DCC1D1||АВВ1А1, то секущая плоскость пересекает грань DCC1D1 по прямой ТЕ, проходящей через точку К параллельно MN.
Решение.
Соединив точки М, Т, Е и N получим искомое сечение – четырёхугольник МТЕN.
Слайд 9Метод следов
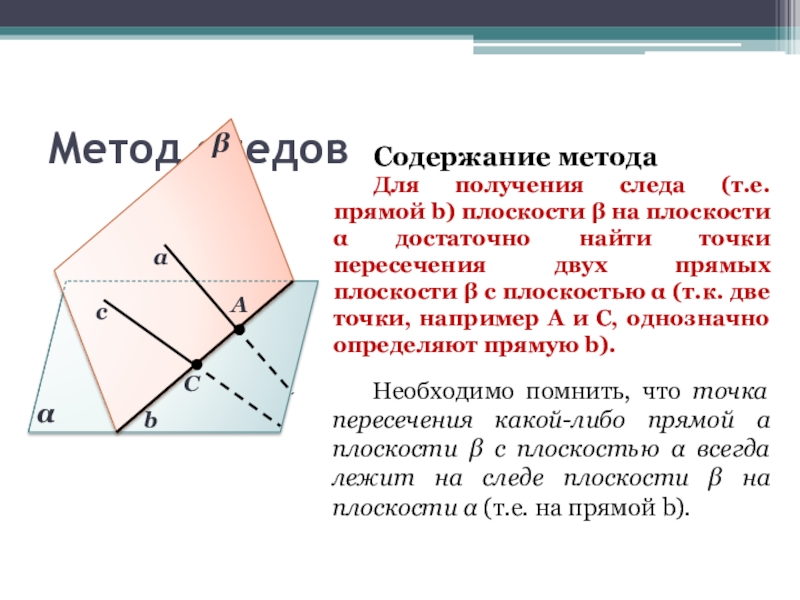
Содержание метода
Сначала строят прямую пересечения секущей плоскости с плоскостью какой-либо
Слайд 10Метод следов
Необходимо помнить, что точка пересечения какой-либо прямой а плоскости
Содержание метода
Для получения следа (т.е. прямой b) плоскости на плоскости достаточно найти точки пересечения двух прямых плоскости с плоскостью (т.к. две точки, например А и С, однозначно определяют прямую b).
Слайд 11Метод следов
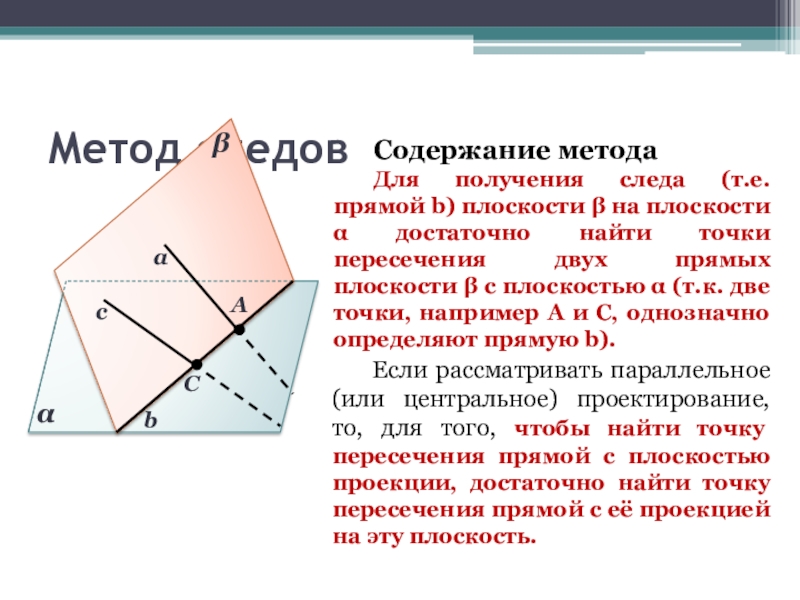
Если рассматривать параллельное (или центральное) проектирование, то, для того, чтобы
Содержание метода
Для получения следа (т.е. прямой b) плоскости на плоскости достаточно найти точки пересечения двух прямых плоскости с плоскостью (т.к. две точки, например А и С, однозначно определяют прямую b).
Слайд 12Задача 3. Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через точки К,
L
М
К
Метод следов
Решение.
Построим проекции точек K, L, M на плоскость основания ABCD. Проекциями будут соответственно точки А, L1 (LL1 || ВВ1) и М.
L1
Слайд 13Задача 3. Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через точки К,
L
М
К
Метод следов
Решение.
Построим проекции точек K, L, M на плоскость основания ABCD. Проекциями будут соответственно точки А, L1 (LL1 || ВВ1) и М.
L1
Построим точку Р пересечения LK и L1А.
Р
Слайд 14Задача 3. Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через точки К,
L
М
К
Метод следов
Решение.
Построим проекции точек K, L, M на плоскость основания ABCD. Проекциями будут соответственно точки А, L1 (LL1 || ВВ1) и М.
L1
Построим точку Р пересечения LK и L1А.
Р
Прямая МР – след секущей плоскости на плоскости основания, а точка Н – точка пересечения МР и АD и ещё одна точка сечения куба.
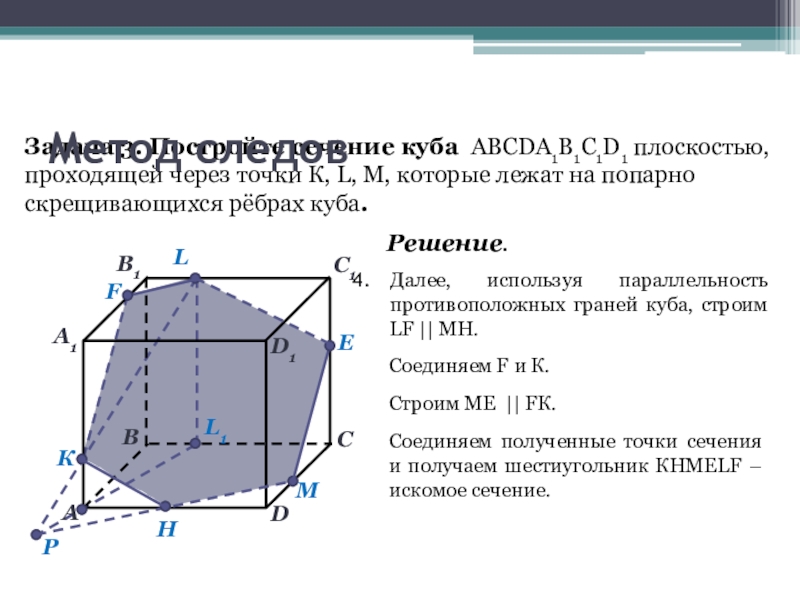
Слайд 15Задача 3. Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через точки К,
L
М
К
Метод следов
Решение.
Далее, используя параллельность противоположных граней куба, строим LF || МН.
L1
Соединяем F и К.
Р
Строим МЕ || FК.
Соединяем полученные точки сечения и получаем шестиугольник КНМЕLF – искомое сечение.
Слайд 16Метод внутреннего проектирования
Содержание метода
Имея три точки, которые определяют плоскость сечения, находят
Слайд 17Метод внутреннего проектирования
Задача 3. Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через
L
М
К
Решение.
Построим проекции точек K, L, M на плоскость основания ABCD. Проекциями будут соответственно точки А, L1 (LL1 || ВВ1) и М.
Будем искать точку Е пресечения секущей плоскости с ребром СС1: проекцией точки Е на плоскость основания является точка С. Соединим четыре точки-проекции отрезками АС и L1М, обозначим точку пересечения Х1.
Х1
Слайд 18Метод внутреннего проектирования
Задача 3. Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через
L
М
К
Решение.
* Точка Х1 – проекция некоторой точки Х секущей плоскости, в которой пересекается прямая LM с пока ещё не определённой прямой КЕ. Проведём через Х1 прямую ХХ1 || LL1, в пересечении ХХ1 и ML получим точку Х.
Х1
Х
Слайд 19Метод внутреннего проектирования
Задача 3. Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через
L
М
К
Решение.
Х1
Х
Теперь проводим прямую КХ до пересечения с ребром СС1 и получаем точку Е.
Е
Дальнейшие построения опираются на параллельность противоположных граней куба, которые секущая плоскость пересекает по параллельным прямым:
Соединяем М и Е.
Строим КF ||МЕ.
F
Соединяем Е и L.
Слайд 20
Метод внутреннего проектирования
Задача 3. Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей
L
М
К
Решение.
Х1
Х
Теперь проводим прямую КХ до пересечения с ребром СС1 и получаем точку Е.
Е
Дальнейшие построения опираются на параллельность противоположных граней куба, которые секущая плоскость пересекает по параллельным прямым:
Строим MH || FL.
F
Соединяем К и Н, L и Е и получаем шестиугольник КНМЕLF – искомое сечение.
H
Слайд 21Применение методов построения сечений многогранников при решении заданий С2
Задача 4
Решение.
Т.к. точки Е, D и D, С1 попарно принадлежат одной грани, можем соединить их отрезками.
Соединяем К и С и получаем четырёхугольник ЕКC1D – искомое сечение.
Е
Т.к. DCC1D1||АВВ1А1, то секущая плоскость пересекает грань АВВ1А1 по прямой ЕК, параллельной DC1.
К
Дальнейшее решение строится на рассмотрении вида четырёхугольника ЕКC1D.
Ответ: 4,5
Слайд 22Применение методов построения сечений многогранников при решении заданий С2
Задача 5 (№161,
Решение.
Проекцией точки S на плоскость основания является точка О.
Применим метод внутреннего проектирования:
Точки Е и Т сечения будут лежать на линиях LL1 и ММ1, параллельных АА1.
С
В
А
С1
В1
А1
S
O
Точки Е и Т сечения будут результатом пересечения BS с LL1 и CS с ММ1 и лежать на соответственных гранях призмы.
Т
Е
Слайд 23Применение методов построения сечений многогранников при решении заданий С2
Задача 5 (№161,
Решение.
Через точки В и Е, С и Т проведём линии сечения на гранях призмы до пересечения с рёбрами верхнего основания и получим четырёхугольник ВКDС – искомое сечение.
С
В
А
С1
В1
А1
S
O
Т
Е
Дальнейшее решение строится на рассмотрении вида четырёхугольника ВКDС.
Слайд 24Применение методов построения сечений многогранников при решении заданий С2
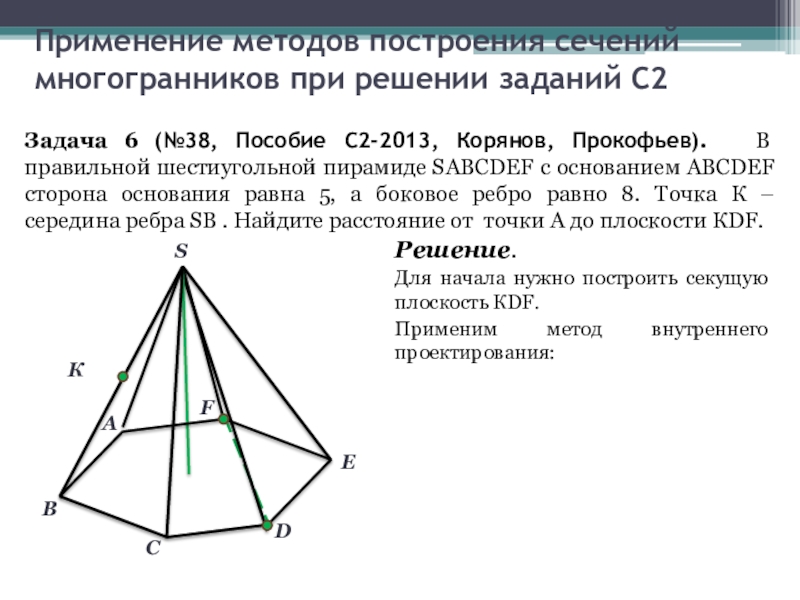
Задача 6 (№38,
Решение.
Применим метод внутреннего проектирования:
Для начала нужно построить секущую плоскость КDF.
Слайд 25Применение методов построения сечений многогранников при решении заданий С2
Задача 6 (№38,
Решение.
Проекцией точки К на плоскость основания является точка Р.
Проекция вспомогательной точки Х, принадлежащей секущей плоскости, будет результатом пересечения ОС и PD.
О
Р
Х
М
FX SC = М – искомая точка секущей плоскости.
Проведём KD и линию, параллельную SO до пересечения с KD – получим вспомогательную точку Х.
Слайд 26Применение методов построения сечений многогранников при решении заданий С2
Задача 6 (№38,
Решение.
Проекция вспомогательной точки Y, принадлежащей секущей плоскости, будет результатом пересечения ОA и PF.
О
Р
DY SA = L – искомая точка секущей плоскости.
Проведём KF и линию, параллельную SO до пересечения с KF – получим вспомогательную точку Y.
Y
L
Слайд 27Применение методов построения сечений многогранников при решении заданий С2
Задача 6 (№38,
Решение.
О
Р
Соединив полученные точки L и M с К, D и F, получим искомую плоскость КDF, (MКLDF – пятиугольник, изображающий искомую плоскость).
L
М
Дальнейшее решение строится на нахождении расстояния от точки А до плоскости пятиугольника MКLDF.
Слайд 28Применение методов построения сечений многогранников при решении заданий С2
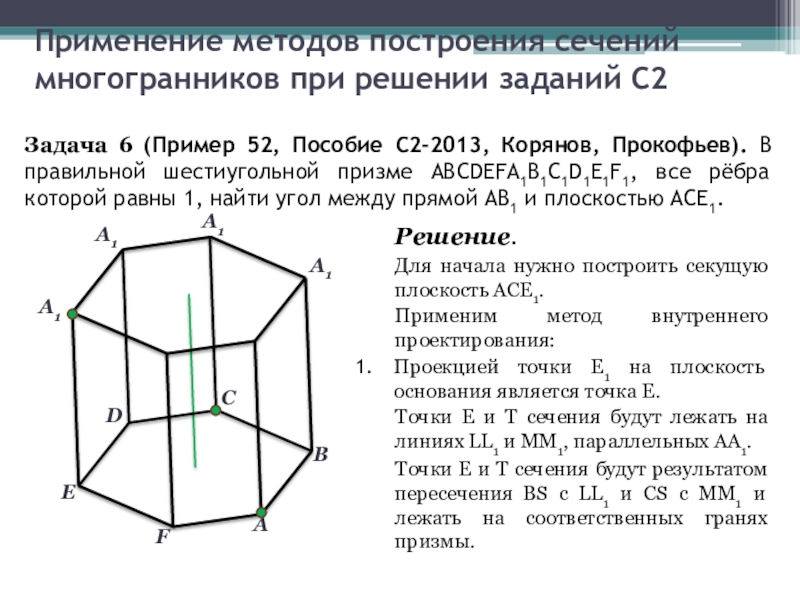
Задача 6 (Пример
Решение.
Проекцией точки Е1 на плоскость основания является точка Е.
Для начала нужно построить секущую плоскость АСЕ1.
Точки Е и Т сечения будут лежать на линиях LL1 и ММ1, параллельных АА1.
Точки Е и Т сечения будут результатом пересечения BS с LL1 и CS с ММ1 и лежать на соответственных гранях призмы.
А
В
С
D
Е
F
Применим метод внутреннего проектирования:
А1
А1
А1
А1
Слайд 29Источники информации
Нелин Е.П. Комплексная подготовка к ЕГЭ и ГИА. Геометрия. 7-11
www.alexlarin.net – сайт по оказанию информационной поддержки студентам и абитуриентам при подготовке к ЕГЭ, поступлению в ВУЗы и изучении различных разделов высшей математики (Пособие для решения заданий С2, авт. Корянов А.Г., Прокофьев А.А.)