- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Котангенс
Содержание
- 1. Презентация по геометрии на тему Котангенс
- 2. 21. 04. 17Классная работаКотангенс
- 3. Изменим геометрическую задачу, с решения которой мы
- 4. Отношение косинуса угла к синусу того же угла рассматривают как ещё одну тригонометрическую функцию — котангенс.
- 5. Определение.Котангенсом угла называется отношение косинуса угла к
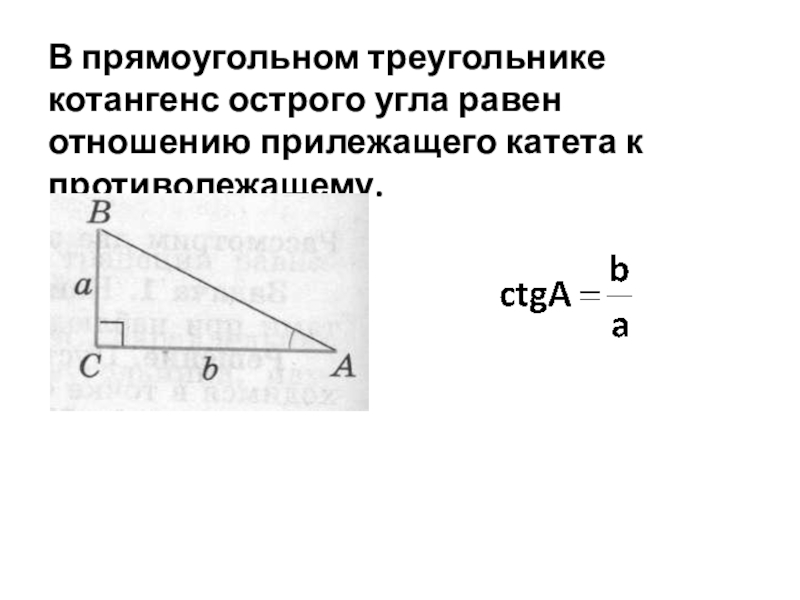
- 6. В прямоугольном треугольнике котангенс острого угла равен отношению прилежащего катета к противолежащему.
- 7. Котангенс не существует тогда, когда синус обращается
- 8. Значения котангенсов конкретных углов находят по таблицам
- 9. При возрастании угла от 0° до 180°
- 10. Справка словесника.Мы познакомились с четырьмя тригонометрическими функциями
- 11. Решение задач№ 8.25; № 8.26; № 8.27; № 8.28(а)
- 12. № 8.25
- 13. № 8.28 Решение. Возьмем центральный прямой угол АОМ,
- 14. Домашнее заданиеn 8. 2№ 8.24; № 8.28
21. 04. 17Классная работаКотангенс
Слайд 3Изменим геометрическую задачу, с решения которой мы начали п. 8.1.
Пусть теперь требуется найти катет АС = b прямоугольного треугольника АBС, зная его катет ВС = а и угол А. Тогда из равенства (1) получим
(6)
Слайд 4
Отношение косинуса угла к синусу того же угла рассматривают как ещё
одну тригонометрическую функцию — котангенс.
Слайд 5Определение.
Котангенсом угла называется отношение косинуса угла к его синусу.
Котангенс обозначается
символом сtg так что по определению
(7)
Слайд 6В прямоугольном треугольнике котангенс острого угла равен отношению прилежащего катета к
противолежащему.
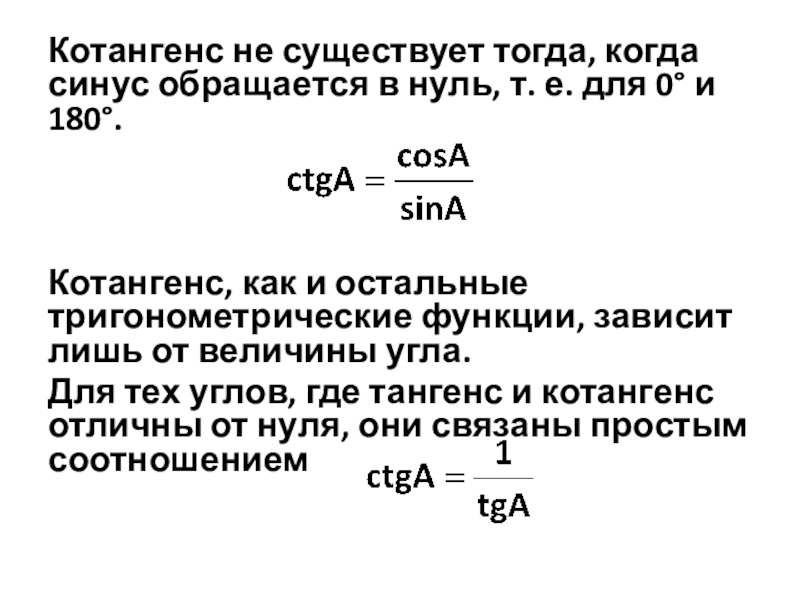
Слайд 7Котангенс не существует тогда, когда синус обращается в нуль, т. е.
для 0° и 180°.
Котангенс, как и остальные тригонометрические функции, зависит лишь от величины угла.
Для тех углов, где тангенс и котангенс отличны от нуля, они связаны простым соотношением
Котангенс, как и остальные тригонометрические функции, зависит лишь от величины угла.
Для тех углов, где тангенс и котангенс отличны от нуля, они связаны простым соотношением
Слайд 8Значения котангенсов конкретных углов находят по таблицам или с помощью калькулятора.
Так
как
sin (180° - α) = sin α и cos (180° - α) = - cos α,
то
ctg(180° - α) = - ctg α
Это равенство связывает котангенсы смежных углов.
sin (180° - α) = sin α и cos (180° - α) = - cos α,
то
ctg(180° - α) = - ctg α
Это равенство связывает котангенсы смежных углов.
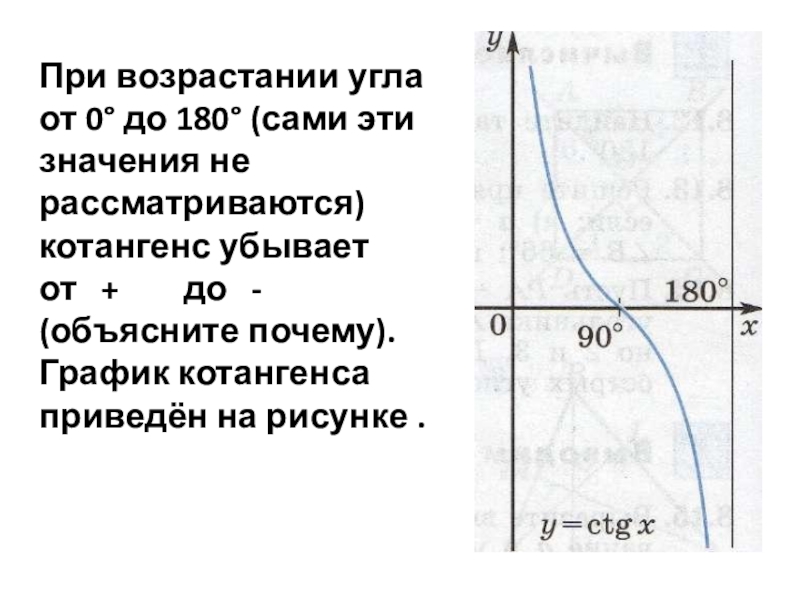
Слайд 9При возрастании угла от 0° до 180° (сами эти значения не
рассматриваются) котангенс убывает от + до - (объясните почему). График котангенса приведён на рисунке .
Слайд 10Справка словесника.
Мы познакомились с четырьмя тригонометрическими функциями — синусом, косинусом, тангенсом
и котангенсом. Приставка ко (со — первые две буквы латинского слова соmplimentus — дополнительный) в названиях функций означает, что эта функция связана с соответствующей ей функцией, в названии которой нет такой приставки, простой зависимостью: для дополнительных острых углов А и В прямоугольного треугольника АBС выполняются равенства
Первое из этих равенств нами доказано в п. 7.3, а второе следует из первого и определений тангенса и котангенса
Первое из этих равенств нами доказано в п. 7.3, а второе следует из первого и определений тангенса и котангенса
Слайд 13№ 8.28
Решение.
Возьмем центральный прямой угол АОМ, из точки М проведем
касательную ME, равную двум радиусам, и точку Е соединим с центром; угол АОВ есть искомый, так как ctg АОВ = ME/R= 2R/R= 2.
Изменив длину радиуса, мы получим треугольник, подобный треугольнику МОЕ, поэтому угол МЕО, а следовательно, и угол АОВ сохранят свою величину.
Изменив длину радиуса, мы получим треугольник, подобный треугольнику МОЕ, поэтому угол МЕО, а следовательно, и угол АОВ сохранят свою величину.
Построить угол, если известно, что его котангенс равен 2 (черт. 7).