- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Конус. Элементы конуса
Содержание
- 1. Презентация по геометрии на тему Конус. Элементы конуса
- 2. Конус – это фигура, полученная вращением прямоугольного треугольника АВС вокруг катета АВ
- 3. Конус (точнее, круговой конус) – это геометрическое
- 4. Элементы конусаОтрезки (или их длины), соединяющие вершину
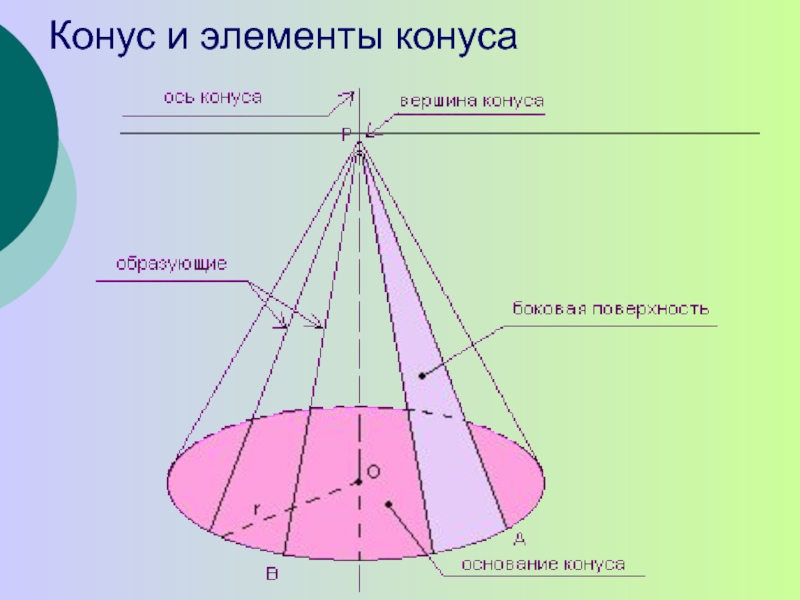
- 5. Конус и элементы конуса
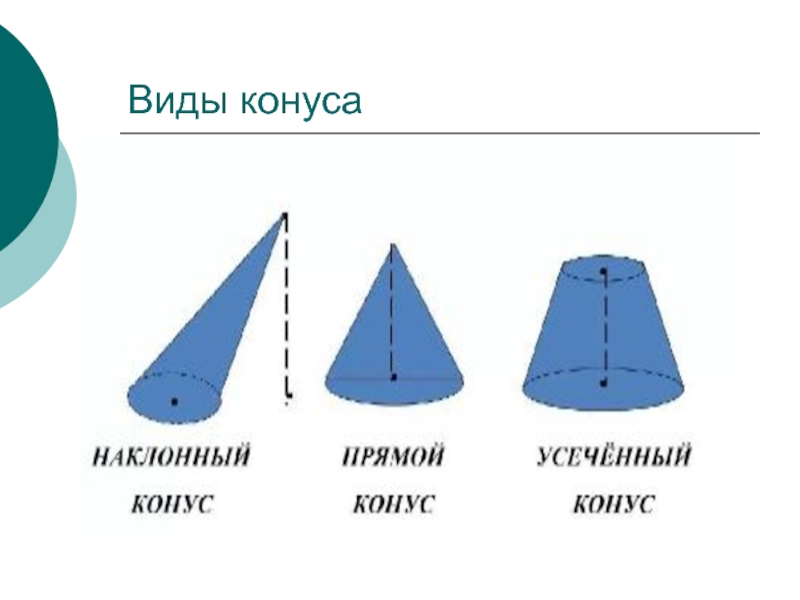
- 6. Виды конуса
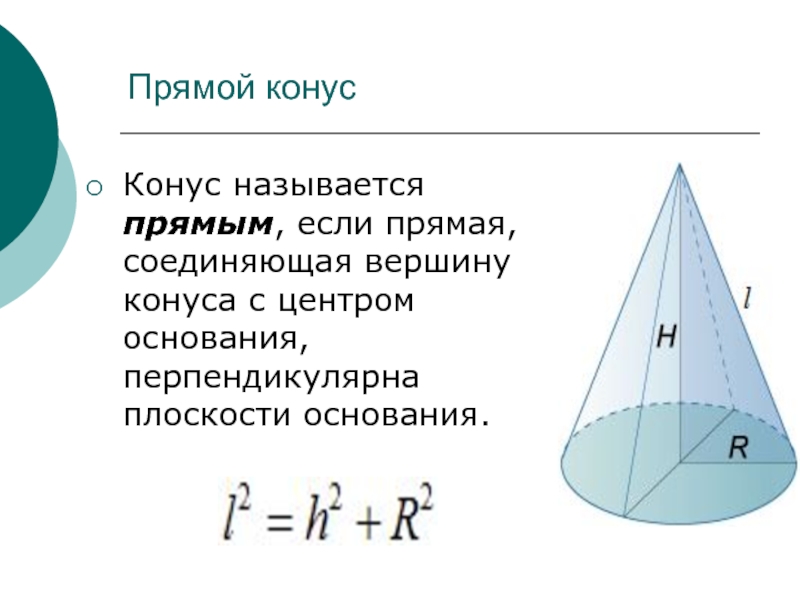
- 7. Прямой конусКонус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.
- 8. Понятия высоты и радиуса конусаРадиусом конуса называется
- 9. Осевое сечение конуса. Если секущая плоскость проходит
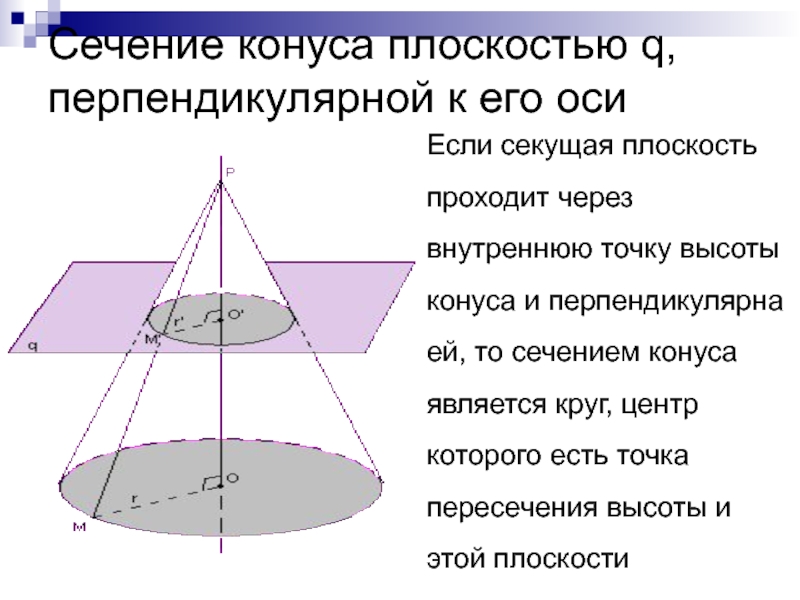
- 10. Сечение конуса плоскостью q, перпендикулярной к его
- 11. Площадь поверхности конусаЗа площадь боковой поверхности конуса
- 12. Слайд 12
- 13. Усечённый конусОпределение. Усечённым конусом называется геометрическая
- 14. Усечённый конусПлоскость, параллельная основанию конуса и пересекающая
- 15. Элементы усеченного конусаОснование исходного конуса и круг,
- 16. Объем усеченного конусаОбъем усеченного конуса равен разности
- 17. Формула вычисления объема усеченного конусаОбъём усечённого конуса
- 18. Площадь боковой поверхности усеченного конусаплощадь боковой поверхности
- 19. Формула для нахождения площади боковой поверхности усеченного
- 20. Формула для нахождения площади полной поверхности усеченного
- 21. Задания№1. Образующая конуса равна 2 см, а
Конус – это фигура, полученная вращением прямоугольного треугольника АВС вокруг катета АВ
Слайд 3
Конус (точнее, круговой конус) – это геометрическое тело, которое состоит из
круга (называемого основанием конуса), точки, не лежащей в плоскости этого круга (называемой вершиной конуса) и всех возможных отрезков, соединяющих вершину конуса с точками основания.
Слайд 4Элементы конуса
Отрезки (или их длины), соединяющие вершину конуса с точками окружности
основания, называются образующими конуса.
Все образующие прямого кругового конуса равны между собой.
Поверхность конуса состоит из основания конуса (круга) и боковой поверхности (составленной из всех возможных образующих).
Объединение образующих конуса называется образующей (или боковой) поверхностью конуса.
Все образующие прямого кругового конуса равны между собой.
Поверхность конуса состоит из основания конуса (круга) и боковой поверхности (составленной из всех возможных образующих).
Объединение образующих конуса называется образующей (или боковой) поверхностью конуса.
Слайд 7Прямой конус
Конус называется прямым, если прямая, соединяющая вершину конуса с центром
основания, перпендикулярна плоскости основания.
Слайд 8Понятия высоты и радиуса конуса
Радиусом конуса называется радиус его основания.
Высотой конуса
называется перпендикуляр (или его длина), опущенный из его вершины на плоскость основания.
У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса является прямая, проходящая через центр основания и вершину.
У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса является прямая, проходящая через центр основания и вершину.
Слайд 9Осевое сечение конуса.
Если секущая плоскость проходит через ось конуса, то
сечение представляет собой равнобедренный треугольник,
основание которого- диаметр основания конуса,
а боковые стороны- образующие конуса. Это сечение- осевое.
основание которого- диаметр основания конуса,
а боковые стороны- образующие конуса. Это сечение- осевое.
Слайд 10Сечение конуса плоскостью q, перпендикулярной к его оси
Если секущая плоскость проходит
через внутреннюю точку высоты конуса и перпендикулярна ей, то сечением конуса является круг, центр которого есть точка пересечения высоты и этой плоскости
Слайд 11
Площадь поверхности конуса
За площадь боковой поверхности конуса принимается площадь её развертки.
Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
S= π r l
Площадь полной поверхности конуса- сумма площадей боковой поверхности и основания.
S= π r (l+r)
Слайд 13Усечённый конус
Определение.
Усечённым конусом называется геометрическая фигура, полученная вращением прямоугольной
трапеции вокруг её меньшей боковой стороны.
Другими словами: усечённым конусом называется часть конуса, заключённая между основанием и параллельным основанию сечением конуса.
Осевое сечение – равнобедренная трапеция
Другими словами: усечённым конусом называется часть конуса, заключённая между основанием и параллельным основанию сечением конуса.
Осевое сечение – равнобедренная трапеция
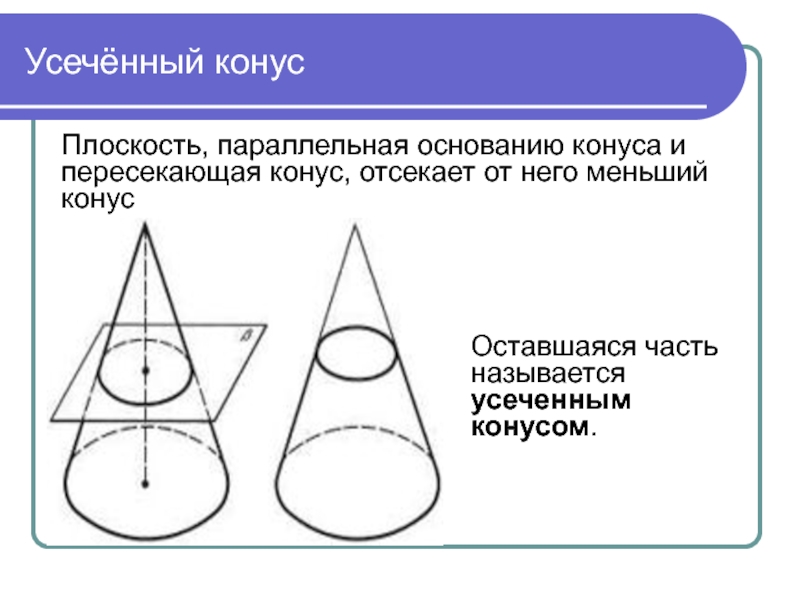
Слайд 14Усечённый конус
Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него
меньший конус
Оставшаяся часть называется усеченным конусом.
Слайд 15Элементы усеченного конуса
Основание исходного конуса и круг, получающийся в сечении этого
конуса плоскостью, называются основаниями, а отрезок, соединяющий их центры - высотой усеченного конуса.
Прямая проходящая через высоту усеченного конуса (т.е. через центры его оснований) является его осью.
Часть боковой поверхности конуса, ограничивающая усеченный конус, называется его боковой поверхностью, а отрезки образующих конуса, расположенные между основаниями усеченного конуса, называются его образующими.
Прямая проходящая через высоту усеченного конуса (т.е. через центры его оснований) является его осью.
Часть боковой поверхности конуса, ограничивающая усеченный конус, называется его боковой поверхностью, а отрезки образующих конуса, расположенные между основаниями усеченного конуса, называются его образующими.
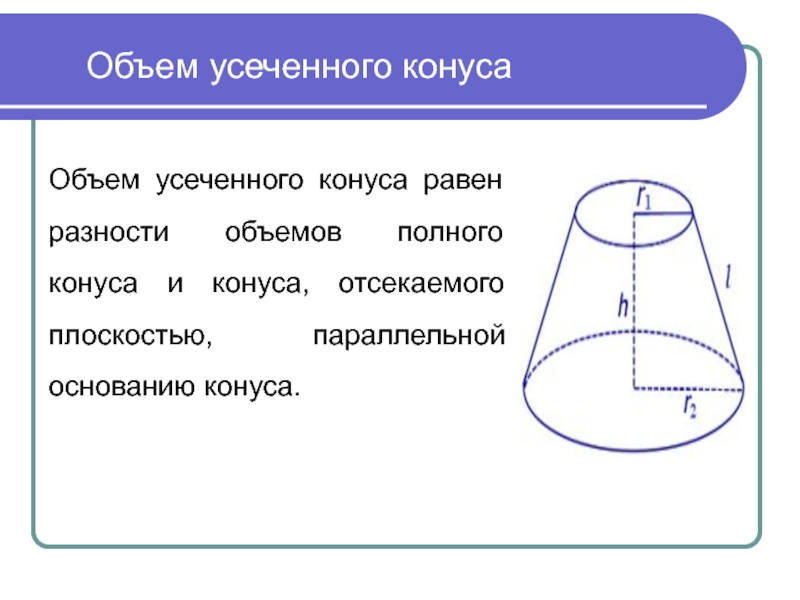
Слайд 16Объем усеченного конуса
Объем усеченного конуса равен разности объемов полного конуса и
конуса, отсекаемого плоскостью, параллельной основанию конуса.
Слайд 17Формула вычисления объема усеченного конуса
Объём усечённого конуса вычисляется по формуле:
где: S1
= πr12 и S2 = πr22 – площади оснований, h – высота усечённого конуса, r1 и r2 – радиусы верхнего и нижнего оснований усеченного конуса.
Слайд 18Площадь боковой поверхности усеченного конуса
площадь боковой поверхности усеченного конуса равна разности
площадей боковых поверхностей полного конуса и конуса, отсекаемого плоскостью, параллельной основанию конуса.
Слайд 19Формула для нахождения площади боковой поверхности усеченного конуса
Площадь боковой поверхности усеченного
конуса вычисляется по формуле:
где: P1 = 2πr1 и P2 = 2πr2 – периметры оснований усеченного конуса, l – длина образующей
где: P1 = 2πr1 и P2 = 2πr2 – периметры оснований усеченного конуса, l – длина образующей
Слайд 20Формула для нахождения площади полной поверхности усеченного конуса
Площадь полной поверхности усеченного
конуса, очевидно, находится как сумма площадей оснований и боковой поверхности:
Слайд 21Задания
№1. Образующая конуса равна 2 см, а радиус основания – 1
см. Объясните, больше или меньше 6 см2 площадь его полной поверхности.
№2. Диаметр основания конуса равен 6, а высота равна 4. Вычислите образующую конуса и расстояние от центра основания до образующей конуса.
№3. В усеченном конусе радиусы оснований равны 1 и 4, а образующая – 5. Найдите высоту конуса.
№2. Диаметр основания конуса равен 6, а высота равна 4. Вычислите образующую конуса и расстояние от центра основания до образующей конуса.
№3. В усеченном конусе радиусы оснований равны 1 и 4, а образующая – 5. Найдите высоту конуса.