март 2015 года.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Использование ИКТ при изучении при обучении геометрии 8-9 классов
Содержание
- 1. Презентация по геометрии на тему Использование ИКТ при изучении при обучении геометрии 8-9 классов
- 2. Слайд 2
- 3. Слайд 3
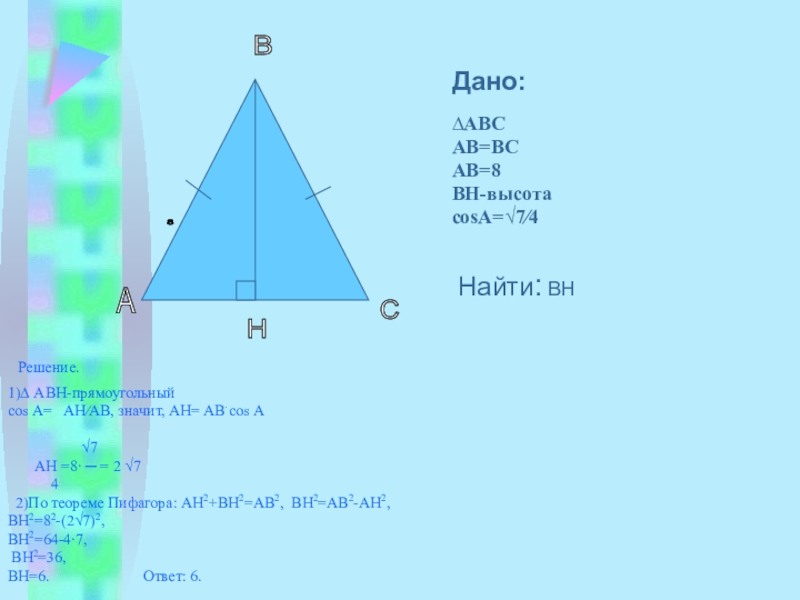
- 4. H A B Решение. 1)∆ АВН-прямоугольный cos
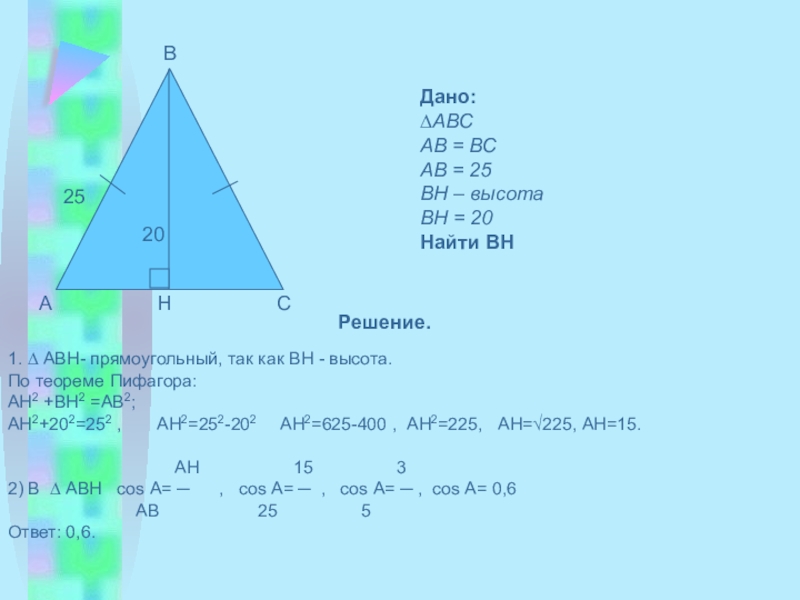
- 5. 2025ABCHДано:∆ABCAB = BCAB = 25BH
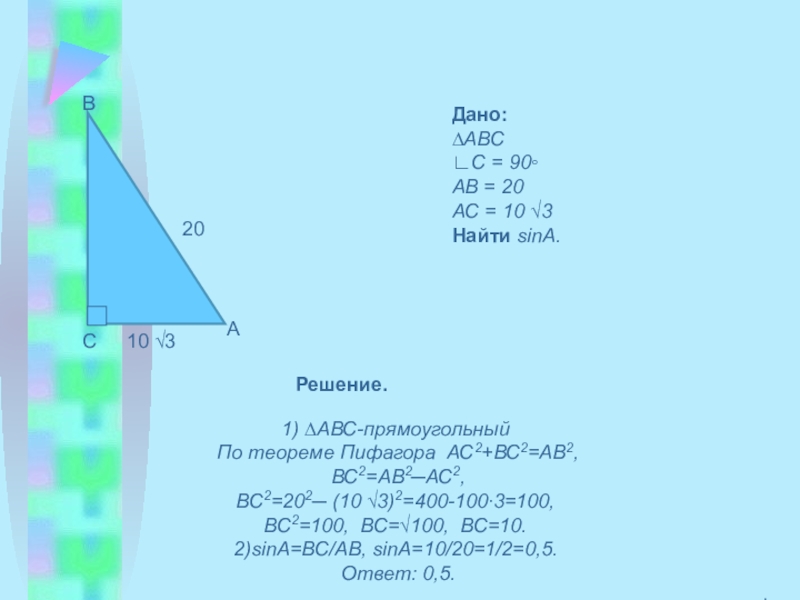
- 6. 20САВ10 √3Дано:∆ABC∟С = 90◦AB = 20AС =
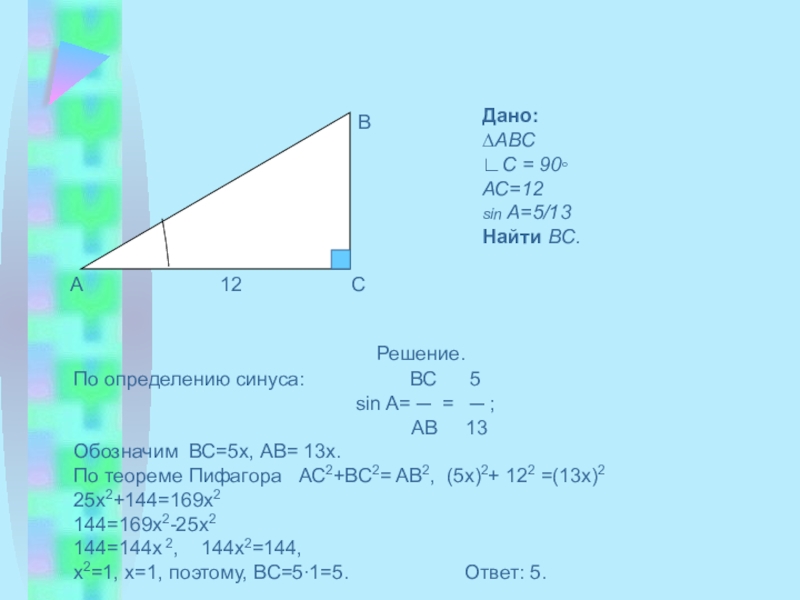
- 7. АCB12Дано:∆ABC∟C = 90◦АС=12sin A=5/13Найти BC.Решение.По определению синуса:
- 8. Второй способ.1)∆АВС –прямоугольный.По основному тригонометрическому тождеству:sin2A+cos2A=
- 9. «Теорема Пифагора»
- 10. №1. Стороны прямоугольника равны 5см и12см .
- 11. №2.Боковая сторона равнобедренного треугольника равна 10см, а
- 12. №3. Периметр ромба 100см, одна из его
- 13. Дано:
- 14. №4. Катеты прямоугольного треугольника 8см и
- 15. Слайд 15
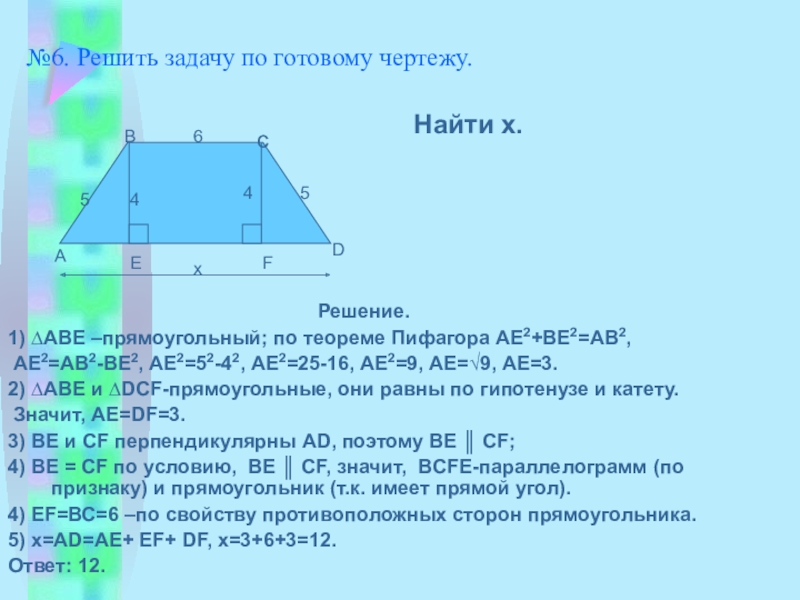
- 16. №6. Решить задачу по готовому чертежу.Найти х.
Презентацию подготовила учитель математики МБОУСОШ №13Матвеева Галина Леонидовна.
Слайд 1 Школьное методобъединение учителей математики, информатики и физики
МБОУСОШ №13.
Презентация на тему:
«Использование ИКТ при обучении геометрии в 8-9 классах».
Слайд 4
H
A
B
Решение.
1)∆ АВН-прямоугольный
cos А= AH∕AB, значит, АН=
АВ۠ cos А
√7
АН =8∙ ─ = 2 √7
4
2)По теореме Пифагора: АН2+ВН2=АВ2, ВН2=АВ2-АН2,
ВН2=82-(2√7)2,
ВН2=64-4∙7,
ВН2=36,
ВН=6. Ответ: 6.
Дано:
∆ABC
AB=BC
AB=8
BH-высота
cosA=√7∕4
C
Найти: BH
8
Слайд 5 20
25
A
B
C
H
Дано:
∆ABC
AB = BC
AB = 25
BH – высота
BH = 20
Найти BH
Решение.
1. ∆ АВН- прямоугольный, так как ВН - высота.
По теореме Пифагора:
АН2 +ВН2 =АВ2; АН2+202=252 , АН2=252-202 АН2=625-400 , АН2=225, АН=√225, АН=15.
АН 15 3
2) В ∆ АВН cos А= ─ , cos А= ─ , cos А= ─ , cos А= 0,6
АВ 25 5
Ответ: 0,6.
Слайд 6
20
С
А
В
10 √3
Дано:
∆ABC
∟С = 90◦
AB = 20
AС = 10 √3
Найти sinА.
Решение.
1) ∆АВС-прямоугольный
По теореме Пифагора АС2+ВС2=АВ2,
ВС2=АВ2─АС2,
ВС2=202─ (10 √3)2=400-100∙3=100,
ВС2=100, ВС=√100, ВС=10.
2)sinA=BC/AB, sinA=10/20=1/2=0,5.
Ответ: 0,5.
.
Слайд 7
А
C
B
12
Дано:
∆ABC
∟C = 90◦
АС=12
sin A=5/13
Найти BC.
Решение.
По определению синуса:
ВС 5
sin A= ─ = ─ ;
АВ 13
Обозначим ВС=5х, AB= 13x.
По теореме Пифагора АС2+ВС2= AB2, (5х)2+ 122 =(13х)2
25х2+144=169х2
144=169х2-25х2
144=144х 2, 144х2=144,
х2=1, х=1, поэтому, ВС=5∙1=5. Ответ: 5.
sin A= ─ = ─ ;
АВ 13
Обозначим ВС=5х, AB= 13x.
По теореме Пифагора АС2+ВС2= AB2, (5х)2+ 122 =(13х)2
25х2+144=169х2
144=169х2-25х2
144=144х 2, 144х2=144,
х2=1, х=1, поэтому, ВС=5∙1=5. Ответ: 5.
Слайд 8 Второй способ.
1)∆АВС –прямоугольный.
По основному тригонометрическому тождеству:
sin2A+cos2A= 1,
cos2A= 1-sin2A,
cos2A=1- (5 ∕ 13)2
25 144 12
cos2A=1─ ─ , cos2A= ─ , cosA= ─ .
169 169 13
sinA 5 12 5 13 5
2)tg A = ─ , tg A= ─ ׃ ─ = ─ ∙ ─ = ─ .
cos A 13 13 13 12 12
3) По определению тангенса:
BC 5
tg A= ─ , значит, ВС= АС∙tgA, ВС= 12∙ ─ = 5.
AC 12
Ответ: 5.
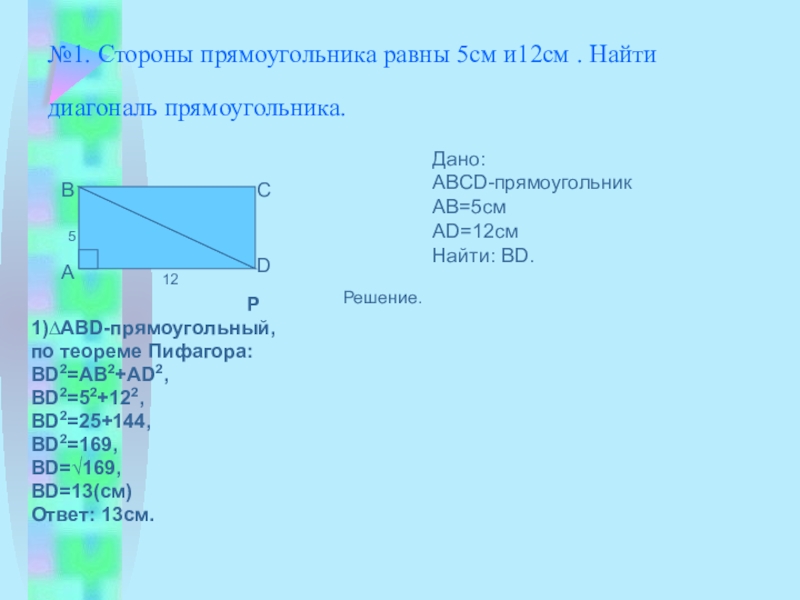
Слайд 10№1. Стороны прямоугольника равны 5см и12см . Найти диагональ прямоугольника.
Р
1)∆АВD-прямоугольный,
по теореме Пифагора:
BD2=АВ2+AD2,
BD2=52+122,
BD2=25+144,
BD2=169,
BD=√169,
BD=13(cм)
Ответ: 13см.
1)∆АВD-прямоугольный,
по теореме Пифагора:
BD2=АВ2+AD2,
BD2=52+122,
BD2=25+144,
BD2=169,
BD=√169,
BD=13(cм)
Ответ: 13см.
D
A
В
С
Дано:
АВСD-прямоугольник
АВ=5см
АD=12см
Найти: ВD.
5
12
Решение.
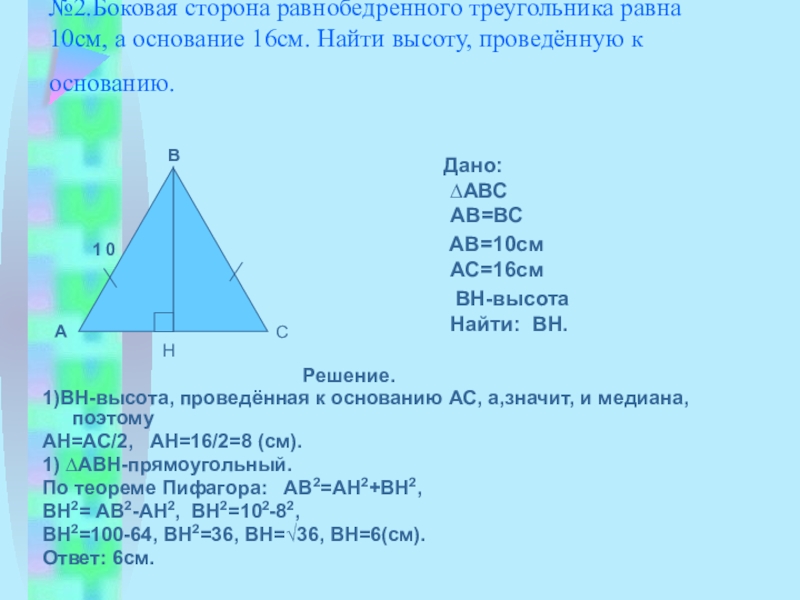
Слайд 11№2.Боковая сторона равнобедренного треугольника равна 10см, а основание 16см. Найти высоту,
проведённую к основанию.
Дано: ∆АВС АВ=ВС
АВ=10см АС=16см
ВН-высота Найти: ВН.
Решение.
1)ВН-высота, проведённая к основанию АС, а,значит, и медиана, поэтому
АН=АС/2, АН=16/2=8 (см).
1) ∆АВН-прямоугольный.
По теореме Пифагора: АВ2=АН2+ВН2,
ВН2= АВ2-АН2, ВН2=102-82,
ВН2=100-64, ВН2=36, ВН=√36, ВН=6(см).
Ответ: 6см.
А
В
С
Н
1
0
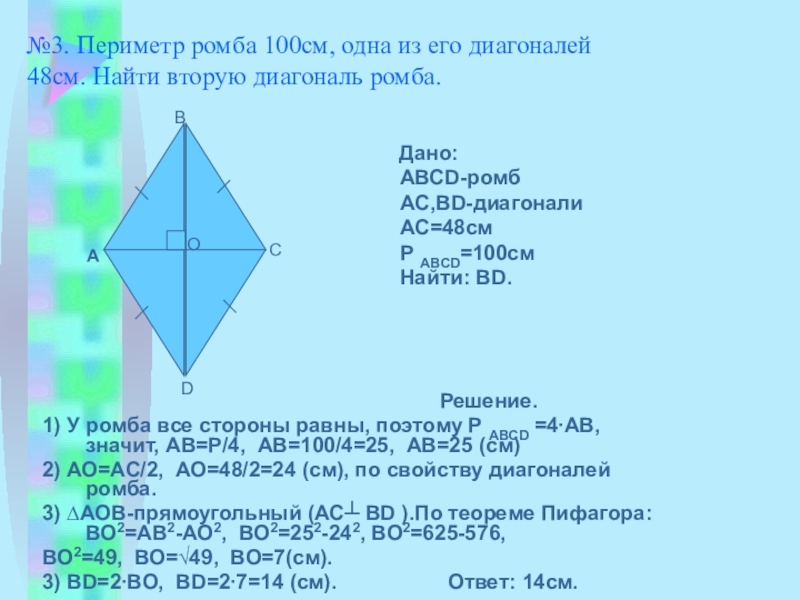
Слайд 12№3. Периметр ромба 100см, одна из его диагоналей 48см. Найти вторую
диагональ ромба.
Дано: АВСD-ромб АС,ВD-диагонали АС=48см Р АВСD=100см Найти: ВD.
Решение.
1) У ромба все стороны равны, поэтому Р АВСD =4∙АВ, значит, АВ=Р/4, АВ=100/4=25, АВ=25 (см)
2) АО=АС/2, АО=48/2=24 (см), по свойству диагоналей ромба.
3) ∆АОВ-прямоугольный (АС┴ ВD ).По теореме Пифагора: ВО2=АВ2-АО2, ВО2=252-242, ВО2=625-576,
ВО2=49, ВО=√49, ВО=7(см).
3) ВD=2∙ВО, ВD=2∙7=14 (см). Ответ: 14см.
А
В
С
D
O
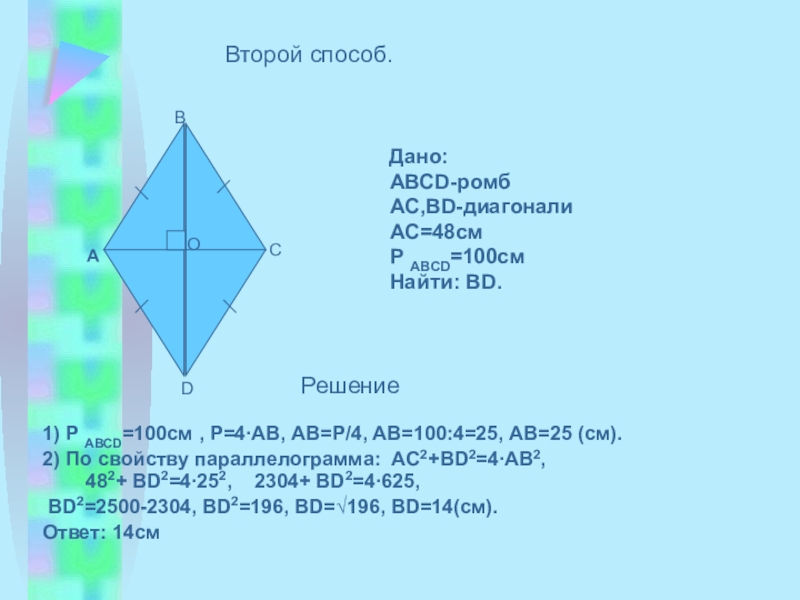
Слайд 13 Дано:
АВСD-ромб АС,ВD-диагонали АС=48см Р АВСD=100см Найти: ВD.
1) Р АВСD=100см , Р=4∙АВ, АВ=Р/4, АВ=100:4=25, АВ=25 (см).
2) По свойству параллелограмма: АС2+ВD2=4∙AB2, 482+ ВD2=4∙252, 2304+ ВD2=4∙625,
ВD2=2500-2304, ВD2=196, ВD=√196, ВD=14(см).
Ответ: 14см
А
В
С
D
O
Второй способ.
Решение
Слайд 14№4. Катеты прямоугольного треугольника 8см и 15 см . Найти медиану,
проведённую к гипотенузе.
Дано: ∆АВС-прямоугольный АС, ВС-катеты АС=8см
ВС=15см
АО=ВО
Найти: СО.
Решение.
1) ∆АВС-прямоугольный (рис.1). По теореме Пифагора:
АВ2=АС2+ВС2, АВ2=82+152, АВ2=64+225, АВ2=289, АВ=√289, АВ=17(см).
2)Построим луч СО, отложим на нём по другую сторону от точки О отрезок ОК, равный отрезку СО (рис.2) . Проведём отрезки ВК и АК.
3)АКВС-параллелограмм (по признаку параллелограмма).
4)В параллелограмме АКВС один из углов –прямой, АКВС-прямоугольник.
5) АВ=СК, по свойству диагоналей прямоугольника. НО тогда АО=ВО=СО=ОК.
АО=АВ/2, АО=17:2=8,5 (см), СО=8,5см. Ответ: 8,5см
А
В
С
О
8
15
В
А
С
О
К
Рис.2
Рис.1
Слайд 15
Решение.
1) По теореме Пифагора: АВ2+ВС2=АС2, АВ=ВС, поэтому, АВ2+АВ2=АС2,
2∙АВ2=АС2, АВ2=АС2/2,
АВ=АС/ √2. (1)
2) АВ=АС/√2, х=12/√2=6√2.
Итак, АВ=ВС=6√2.
Ответ: 6√2.
Из решённой задачи полезно запомнить формулу (1).
Если обозначить гипотенузу прямоугольного равнобедренного треугольника
через а, то его катет х можно найти по формуле: а
х= ─
√2
1) По теореме Пифагора: АВ2+ВС2=АС2, АВ=ВС, поэтому, АВ2+АВ2=АС2,
2∙АВ2=АС2, АВ2=АС2/2,
АВ=АС/ √2. (1)
2) АВ=АС/√2, х=12/√2=6√2.
Итак, АВ=ВС=6√2.
Ответ: 6√2.
Из решённой задачи полезно запомнить формулу (1).
Если обозначить гипотенузу прямоугольного равнобедренного треугольника
через а, то его катет х можно найти по формуле: а
х= ─
√2
С
А
В
12
х
х
Найти Х.
№5
Слайд 16№6. Решить задачу по готовому чертежу.
Найти х.
Решение.
1) ∆АВЕ –прямоугольный; по теореме Пифагора АЕ2+ВЕ2=АВ2,
АЕ2=АВ2-ВЕ2, АЕ2=52-42, АЕ2=25-16, АЕ2=9, АЕ=√9, АЕ=3.
2) ∆АВЕ и ∆DСF-прямоугольные, они равны по гипотенузе и катету.
Значит, АЕ=DF=3.
3) ВЕ и СF перпендикулярны АD, поэтому ВЕ ║ СF;
4) ВЕ = СF по условию, ВЕ ║ СF, значит, BCFE-параллелограмм (по признаку) и прямоугольник (т.к. имеет прямой угол).
4) ЕF=ВС=6 –по свойству противоположных сторон прямоугольника.
5) х=АD=АЕ+ ЕF+ DF, х=3+6+3=12.
Ответ: 12.
1) ∆АВЕ –прямоугольный; по теореме Пифагора АЕ2+ВЕ2=АВ2,
АЕ2=АВ2-ВЕ2, АЕ2=52-42, АЕ2=25-16, АЕ2=9, АЕ=√9, АЕ=3.
2) ∆АВЕ и ∆DСF-прямоугольные, они равны по гипотенузе и катету.
Значит, АЕ=DF=3.
3) ВЕ и СF перпендикулярны АD, поэтому ВЕ ║ СF;
4) ВЕ = СF по условию, ВЕ ║ СF, значит, BCFE-параллелограмм (по признаку) и прямоугольник (т.к. имеет прямой угол).
4) ЕF=ВС=6 –по свойству противоположных сторон прямоугольника.
5) х=АD=АЕ+ ЕF+ DF, х=3+6+3=12.
Ответ: 12.
А
В
с
D
5
5
6
Е
F
4
4
х
