СОШ №14
Ефремов Демид
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Геометрия в разрезе(7 класс)
Содержание
- 1. Презентация по геометрии на тему Геометрия в разрезе(7 класс)
- 2. Увлечение математикой часто начинается с размышления над какой-то особенно понравившейся задачей.
- 3. Актуальность. Техника разрезания дает первоначальный
- 4. Гипотеза.«Простая техника задач на разрезание помогает в решении задач и доказательстве теорем по геометрии».
- 5. Цель и задачи.Цель: доказать, что простая техника
- 6. Объект исследования: задачи на разрезание. Предмет исследования:
- 7. История задач на разрезание. Задачи
- 8. История задач на разрезание.Гильберт.Третья проблема Соломон Голомб 1953 год. Головоломка «полимино»
- 9. Виды задач на разрезание. Головоломки на разрезание
- 10. Задачи на разрезание В основе решения этих
- 11. Задачи на разрезание на клетчатой бумагеПопробуйте разрезать
- 12. Задачи на разрезание и перекраивание фигур:а) данный
- 13. Задания из ЕГЭ.Найдите площадь треугольника АВС, считая стороны квадратных клеток равными 1.АВСВD
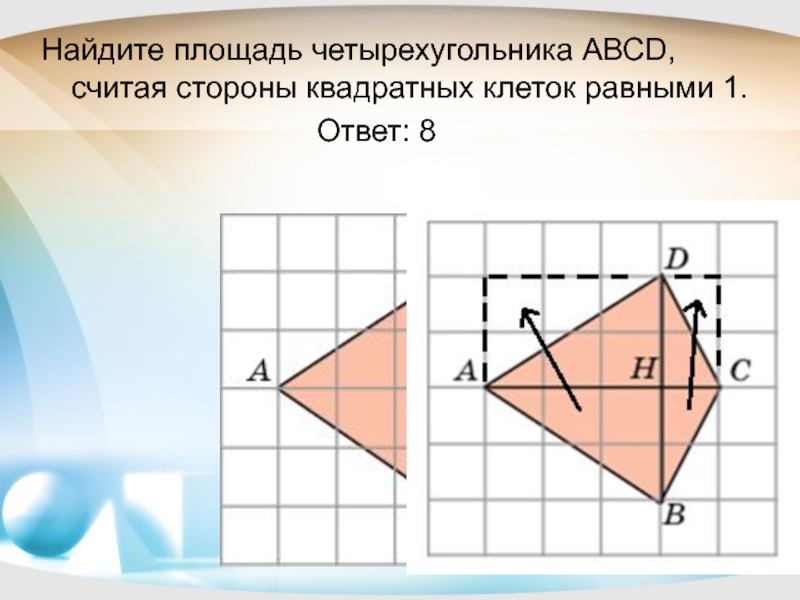
- 14. Найдите площадь четырехугольника АВСD, считая стороны квадратных
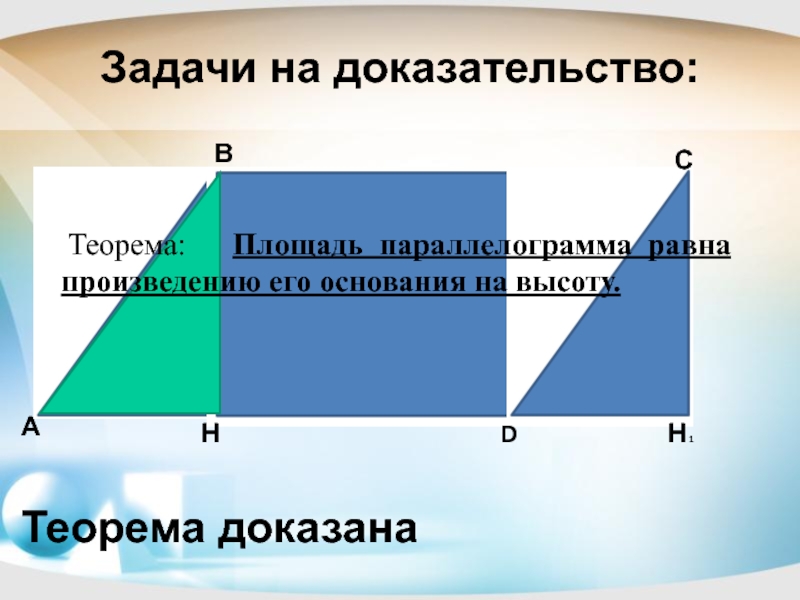
- 15. Задачи на доказательство:АВDСН 1Н Теорема доказана Теорема: Площадь параллелограмма равна произведению его основания на высоту.
- 16. Выводы: «Геометрия полна приключений, потому
- 17. Спасибо за внимание
Увлечение математикой часто начинается с размышления над какой-то особенно понравившейся задачей.
Слайд 2 Увлечение математикой часто начинается с размышления над какой-то
особенно понравившейся задачей.
Слайд 3Актуальность.
Техника разрезания дает первоначальный опыт математического моделирования.
При решении задач мы знакомимся с методами математических рассуждений, расширяем кругозор находим общие методы для решения различных задач.
ЕГЭ!
Слайд 4Гипотеза.
«Простая техника задач на разрезание помогает в решении задач и доказательстве
теорем по геометрии».
Слайд 5Цель и задачи.
Цель: доказать, что простая техника задач на разрезание может
решить математические задачи простыми наглядными методами.
Задачи:
узнать историю и освоить технику задач на разрезание;
выявить связь задач на разрезание и геометрии;
решить задачи и доказать некоторые теоремы геометрии с использованием техники задач на разрезание;
показать применение техники разрезания и перекраивания в заданиях ОГЭ и ЕГЭ.
Задачи:
узнать историю и освоить технику задач на разрезание;
выявить связь задач на разрезание и геометрии;
решить задачи и доказать некоторые теоремы геометрии с использованием техники задач на разрезание;
показать применение техники разрезания и перекраивания в заданиях ОГЭ и ЕГЭ.
Слайд 6Объект исследования: задачи на разрезание.
Предмет исследования: методы и приёмы решения
задач на разрезание.
Методы исследования.
Сравнение;
Сопоставление;
Физический опыт;
Анализ;
Обобщение;
Моделирование.
Слайд 7История задач на разрезание.
Задачи на разрезание, как один
из видов головоломок, привлекали к себе внимание с древнейших времен.
II в. до н.э. «Начала» Евклид
X век. Первый трактат Абу аль – Вефа.
Слайд 8История задач на разрезание.
Гильберт.
Третья проблема
Соломон Голомб
1953 год.
Головоломка «полимино»
Слайд 9Виды задач на разрезание.
Головоломки на разрезание и складывание.
Танграм
Полимино— плоские геометрические фигуры,
образованные путём соединения нескольких одноклеточных квадратов по их сторонам.
Головоломка "Танграм" - квадрат, разрезанный на 7 частей из которых составляют различные силуэты, которые складывают определённым образом для получения другой.
Слайд 10Задачи на разрезание
В основе решения этих задач лежит применение аксиомы:
«Прямая разбивает плоскость на две полуплоскости».
«Семь раз отмерь, один раз отрежь!» - эта пословица предостерегает нас от поспешности в решении задач.
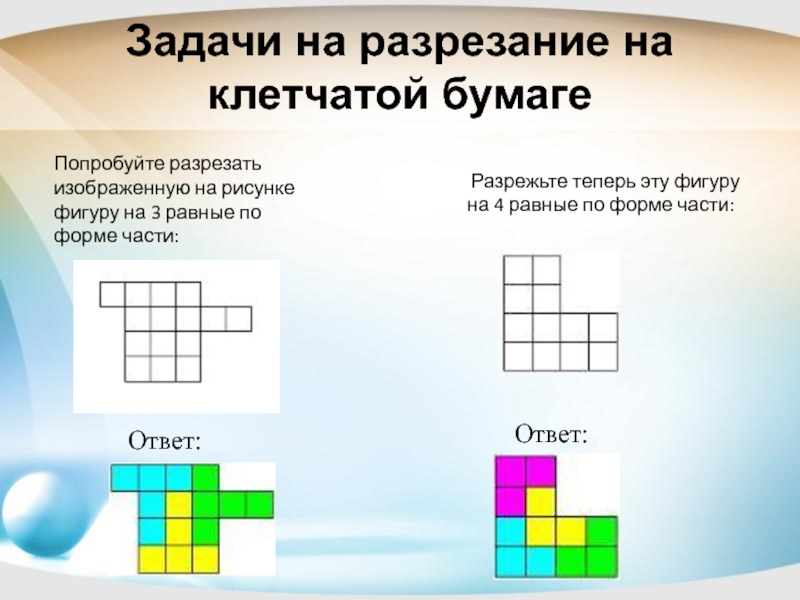
Слайд 11Задачи на разрезание на клетчатой бумаге
Попробуйте разрезать изображенную на рисунке фигуру
на 3 равные по форме части:
Ответ:
Разрежьте теперь эту фигуру на 4 равные по форме части:
Ответ:
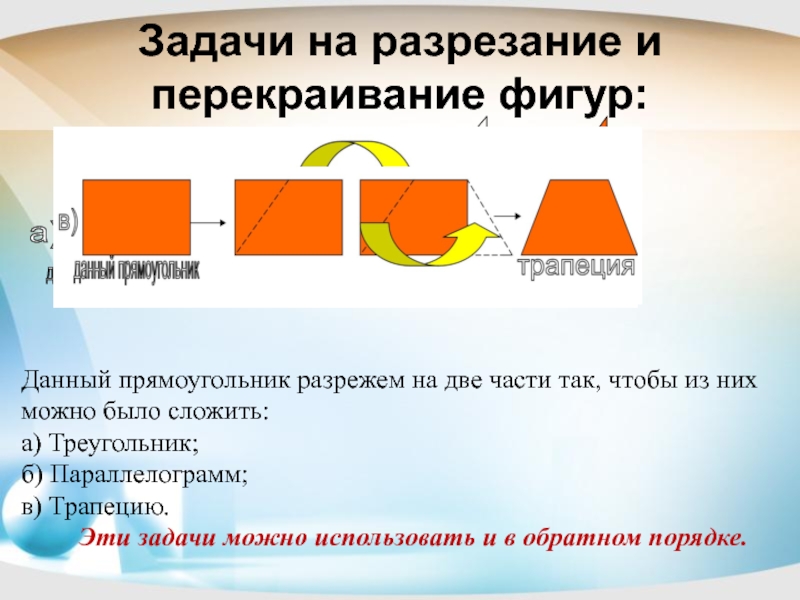
Слайд 12Задачи на разрезание и перекраивание фигур:
а)
данный прямоугольник
треугольник
Данный прямоугольник
разрежем на две части так, чтобы из них можно было сложить:
а) Треугольник;
б) Параллелограмм;
в) Трапецию.
Эти задачи можно использовать и в обратном порядке.
а) Треугольник;
б) Параллелограмм;
в) Трапецию.
Эти задачи можно использовать и в обратном порядке.
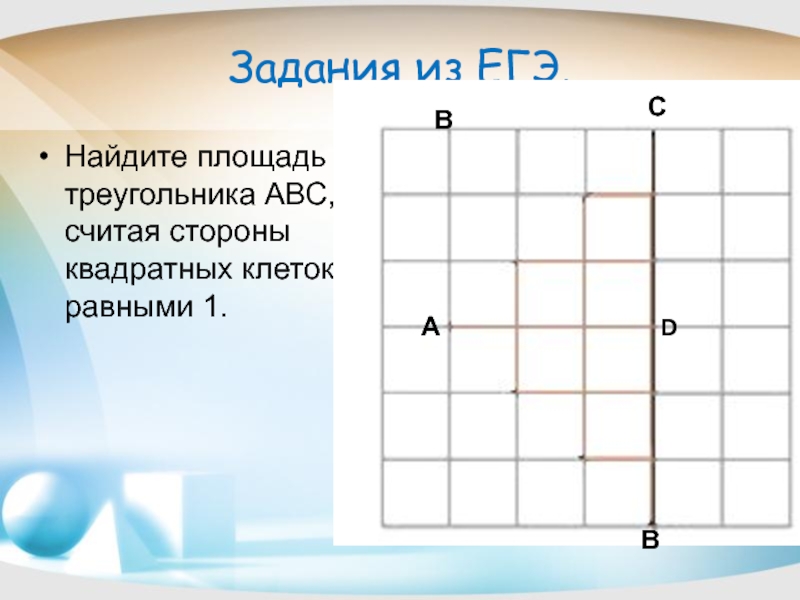
Слайд 13Задания из ЕГЭ.
Найдите площадь треугольника АВС, считая стороны квадратных клеток равными
1.
А
В
С
В
D
Слайд 15Задачи на доказательство:
А
В
D
С
Н 1
Н
Теорема доказана
Теорема: Площадь параллелограмма равна
произведению его основания на высоту.
Слайд 16Выводы:
«Геометрия полна приключений, потому что за каждой задачей
скрывается приключение мысли. Решить задачу – это значит пережить приключение».
Задачи на разрезание появились в древние времена, но ими так увлекаются и до сих пор.
Многие задачи по геометрии можно решить, не используя формулы, а применяя метод разрезания и перекраивания.
Улучшают пространственное воображение.
Знакомят на практике с основными геометрическими понятиями.
Задачи на разрезание могут помочь при нахождении геометрических величин и доказательстве теорем.
Технику задач на разрезание можно применить для решения задач на ЕГЭ.
Развивают творческие способности.
Моя гипотеза подтвердилась.
