- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Формулы вычисление площадей геометрических фигур (8 класс)
Содержание
- 1. Презентация по геометрии на тему Формулы вычисление площадей геометрических фигур (8 класс)
- 2. Цели и задачи урокаПовторить основные формулы вычисления
- 3. Вспомним формулы:Площадь прямоугольникаПараллелограмма;Трапеции;Ромба;Прямоугольного треугольника;ТреугольникаквадратаS =a*bS = a*hS
- 4. Периметр квадратаПериметр прямоугольника;Теореме Пифагора;Как найти катет по
- 5. ЗапомнитьS =
- 6. Решить № 499А)а=24см в = 25см с = 7 смP= (24+25+7)/2 =28
- 7. Боковые стороны трапеции равны 9 см и
- 8. АDВСНО30 см.15 см.12 см.9 см.Решение.1Проведем BH ⎪⎪CD,
- 9. Решение задач по готовым чертежам.1.ABCD - параллелограмм. Найти: ВЕ.ACBDE45°4
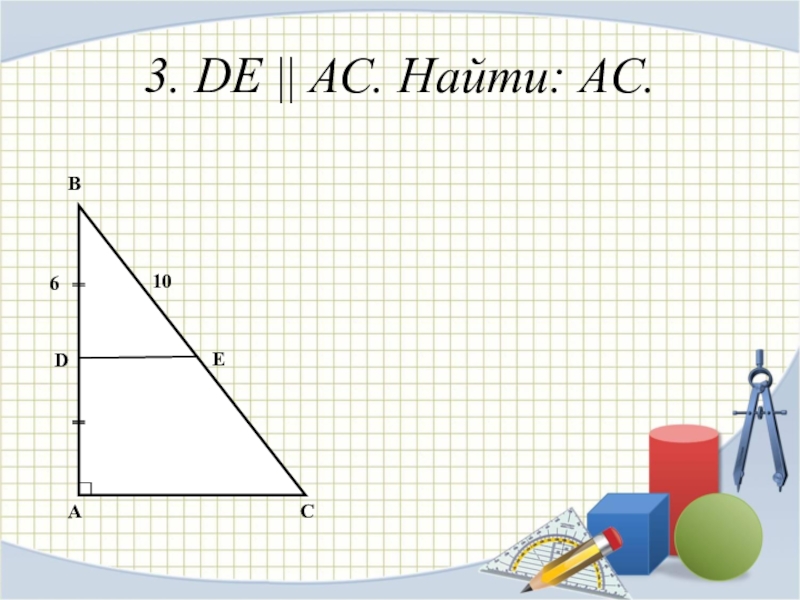
- 10. 3. DE || АС. Найти: AC.ABCDE610
- 11. 4.Найдите площадь треугольника со сторонами 5, 6,
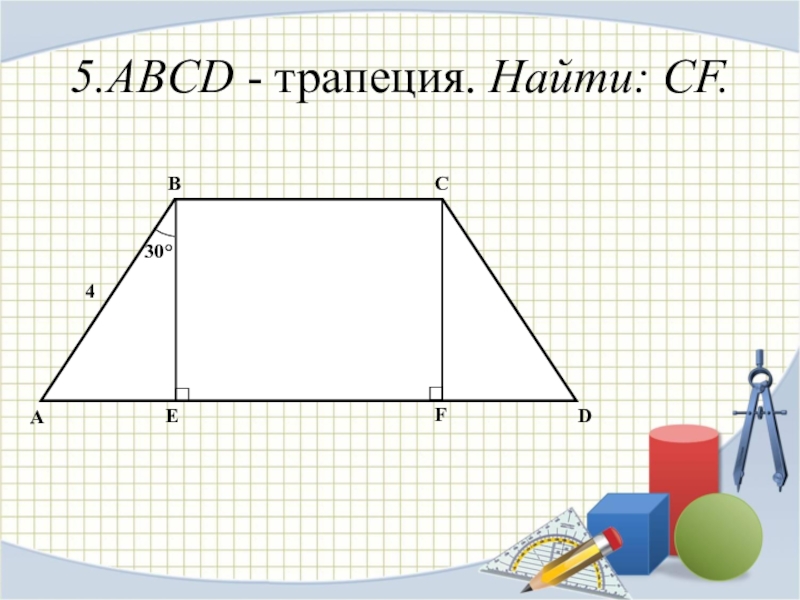
- 12. 5.ABCD - трапеция. Найти: CF.ABCDEF430°
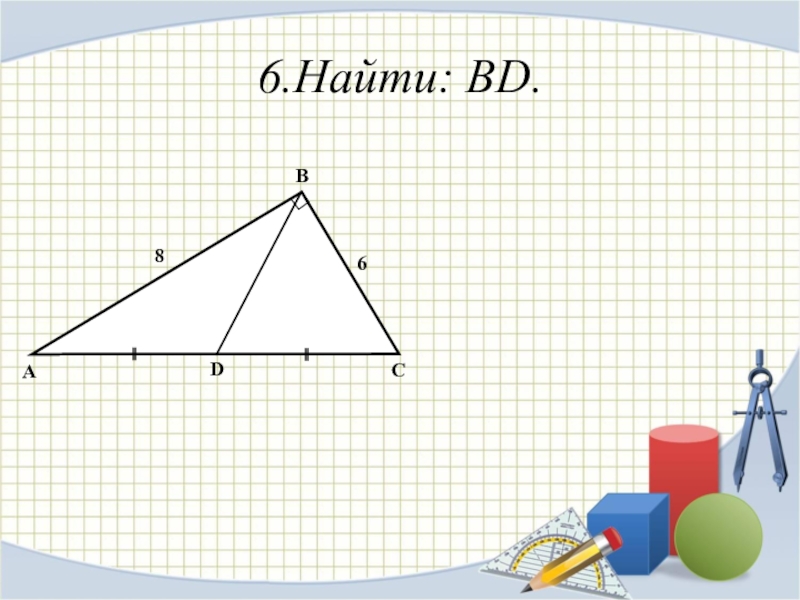
- 13. 6.Найти: BD.ABCD86
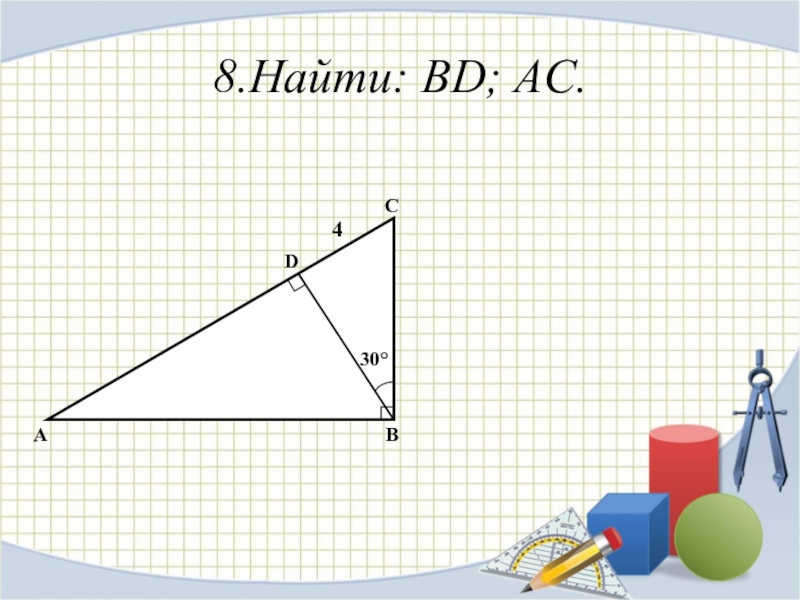
- 14. 8.Найти: BD; AC.ABCD30°4
- 15. Боковая сторона равнобедренного треугольника равна 17 см,
- 16. Самостоятельная работа2 уровень171.Найти: площадь трапеции.I вариантII вариант202.В
Цели и задачи урокаПовторить основные формулы вычисления площадей известных фигур;Решать задачи, используя изученные формулы;Познакомить с формулой Герона;Подготовиться к контрольной работе
Слайд 2Цели и задачи урока
Повторить основные формулы вычисления площадей известных фигур;
Решать задачи,
используя изученные формулы;
Познакомить с формулой Герона;
Подготовиться к контрольной работе
Познакомить с формулой Герона;
Подготовиться к контрольной работе
Слайд 3Вспомним формулы:
Площадь прямоугольника
Параллелограмма;
Трапеции;
Ромба;
Прямоугольного треугольника;
Треугольника
квадрата
S =a*b
S = a*h
S = (a+b)/2 *h
S =
1/2d1*d2
S =1/2 a*b
S = 1/2a*h
S = a*a
S =1/2 a*b
S = 1/2a*h
S = a*a
Слайд 4Периметр квадрата
Периметр прямоугольника;
Теореме Пифагора;
Как найти катет по теореме Пифагора;
P= 4a
P =
2(a+b)
c2 =a2 +b2
b2 =c2 - a2
c2 =a2 +b2
b2 =c2 - a2
Слайд 7Боковые стороны трапеции равны 9 см и 12 см, а основания
30 см и 15 см. Найдите угол, который образуют продолжения боковых сторон трапеции
Слайд 8
А
D
В
С
Н
О
30 см.
15 см.
12 см.
9 см.
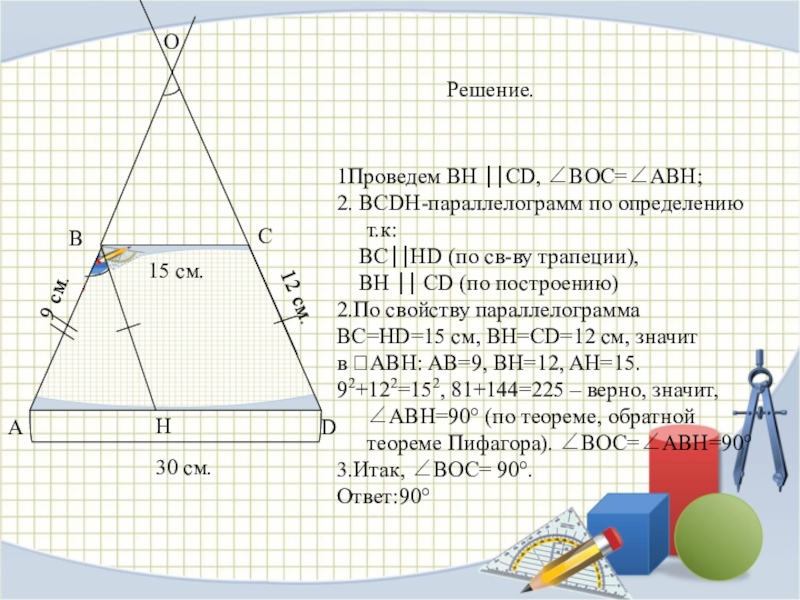
Решение.
1Проведем BH ⎪⎪CD, ∠BOC=∠ABH;
2. ВСDН-параллелограмм по определению
т.к:
ВС⎪⎪НD (по св-ву трапеции),
ВН ⎪⎪ СD (по построению)
2.По свойству параллелограмма
ВС=НD=15 см, BH=CD=12 см, значит
в ABH: AB=9, BH=12, AH=15.
92+122=152, 81+144=225 – верно, значит, ∠ABH=90° (по теореме, обратной теореме Пифагора). ∠BOC=∠ABH=90°
3.Итак, ∠BOC= 90°.
Ответ:90°
ВС⎪⎪НD (по св-ву трапеции),
ВН ⎪⎪ СD (по построению)
2.По свойству параллелограмма
ВС=НD=15 см, BH=CD=12 см, значит
в ABH: AB=9, BH=12, AH=15.
92+122=152, 81+144=225 – верно, значит, ∠ABH=90° (по теореме, обратной теореме Пифагора). ∠BOC=∠ABH=90°
3.Итак, ∠BOC= 90°.
Ответ:90°
Слайд 15
Боковая сторона равнобедренного треугольника равна 17 см, а биссектриса, проведенная к
основанию – 15 см. Найдите площадь и периметр этого треугольника.
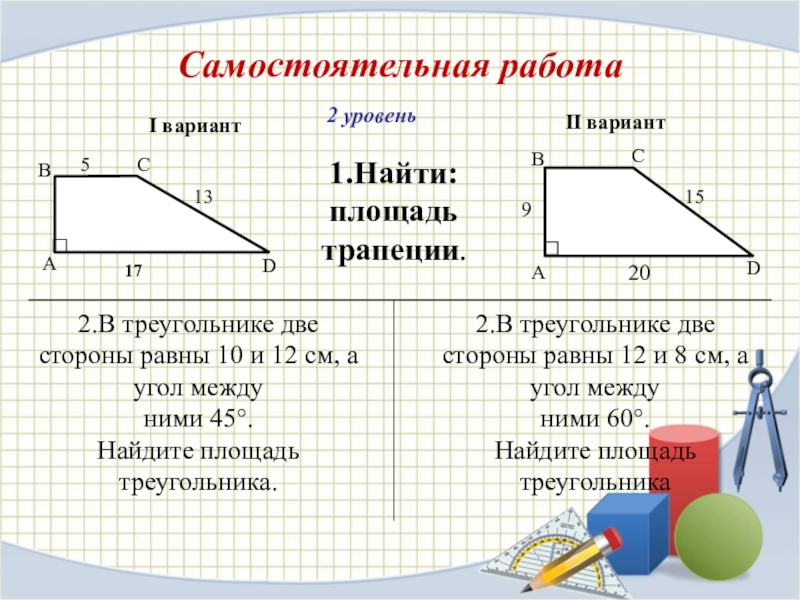
Слайд 16Самостоятельная работа
2 уровень
17
1.Найти: площадь трапеции.
I вариант
II вариант
20
2.В треугольнике две стороны равны
10 и 12 см, а угол между
ними 45°.
Найдите площадь треугольника.
Найдите площадь треугольника.
5
13
А
B
C
D
А
B
C
D
2.В треугольнике две стороны равны 12 и 8 см, а угол между
ними 60°.
Найдите площадь треугольника
9
15