- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Формула Герона
Содержание
- 1. Презентация по геометрии на тему Формула Герона
- 2. Герон Александрийский -древнегреческий математик и механик, живший, вероятно, в 1 в. н. э.
- 3. Теорема. Площадь S треугольника, стороны которого
- 4. Из уравнения (1) получаем, что 2ax=a2+c2-b2,Поскольку AD2=AB2-BD2,
- 5. Слайд 5
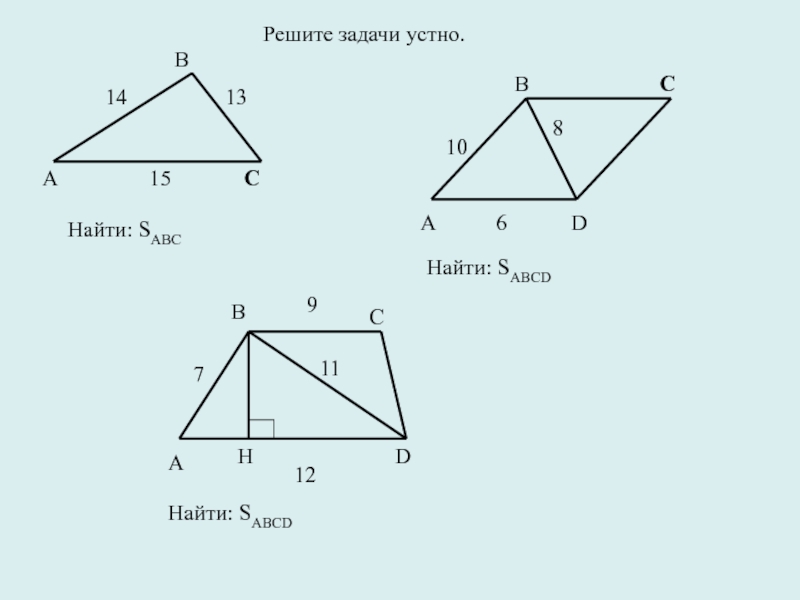
- 6. Решите задачи устно.
- 7. Задача №504. Меньшая сторона параллелограмма равна 29см.
- 8. Задача №517. Найдите площадь четырехугольника ABCD, если
- 9. 2 способВ треугольнике АВС ВС2=АВ2+АС2, поэтому треугольник
Слайд 3Теорема. Площадь S треугольника, стороны которого равны
где p – полупериметр треугольника.
Дано: ABC, AB=c, AC=b, BC=a
p –полупериметр АВС.
Док-ть:
Доказательство.
Проведем высоту АD треугольника ABC.
Введем обозначения: AD=h,
BD=x, тогда DC=a-x.
По теореме Пифагора AD2=AB2-BD2 и AD2=AC2-CD2. Поэтому AB2-BD2=AC2-CD2, то есть c2-x2=b2-(a-x)2. (1)
Слайд 4Из уравнения (1) получаем, что 2ax=a2+c2-b2,
Поскольку AD2=AB2-BD2, то h2=c2-x2 (2) и
D
h
x
a-x
c2-x2=b2-(a-x)2 (1)
(3)
Последовательно раскладывая на множители разность квадратов в числителе правой части равенства (3), получаем:
(4)
Периметр a+b+c треугольника ABC обозначим 2p. Получим
a+b-c=2p-2c, a+c-b=2p-2b, b+c-a=2p-2a. Поэтому окончательно
Так как площадь S треугольника АВС выражается формулой S=0,5ah, то, подставляя в нее h по формуле (5), получаем, что
(5)
Слайд 7Задача №504. Меньшая сторона параллелограмма равна 29см. Перпендикуляр, проведенный из точки
Дано: АВСD – параллелограмм, АВ=29см,
АС, ВD – диагонали, АС BD=O,
АК AD, AK=33см, KD=12см.
Найти: SABCD.
Решение.
В треугольнике ABD проведем BH AD.
H
По теореме Фалеса HK=KD=12cм.
Тогда AH=AK-HK=33-12=21(cм).
В прямоугольном треугольнике ABH по теореме Пифагора имеем:
SABCD=AD·BH=45·20=900(см2)
Слайд 8Задача №517. Найдите площадь четырехугольника ABCD, если AB=5см, BC=13см, CD=9см, DA=15см,
Применим к треугольникам ABC и ACD формулу Герона.
SABCD=SABC+SACD=30+54=84(см2)
1 способ
Слайд 92 способ
В треугольнике АВС ВС2=АВ2+АС2, поэтому треугольник АВС прямоугольный с гипотенузой
SABC=0,5AB·AC=0,5·5·12=30(см2)
Аналогично доказывается, что треугольник ACD прямоугольный
SACD=0,5AC·CD=0,5·12·9=54(см2)
SABCD=84(см2)