и плоскостью?
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Двугранный угол
Содержание
- 1. Презентация по геометрии на тему Двугранный угол
- 2. Вопрос № 1.Сформулируйте теорему о трёх перпендикулярах.
- 3. Вопрос №2.Постройте куб АВСДА¹В¹С¹Д¹(1вариант) и МNOPM¹N¹O¹P¹( 2вариант).Укажите
- 4. Рассмотрим два полупространства , образованных непараллельными плоскостями
- 5. Прямую , по которой пересекаются плоскости –
- 6. Двугранный угол с гранями α , β
- 7. Для измерения двугранного угла введём понятие его
- 8. аαβОАВТак как ОА ⊥ а ,ОВ ⊥а
- 9. Теорема : Величина линейного угла не зависит
- 10. Двугранный угол является острым , прямым или
- 11. Двугранный угол является острым , прямым или
- 12. Двугранный угол является острым , прямым или
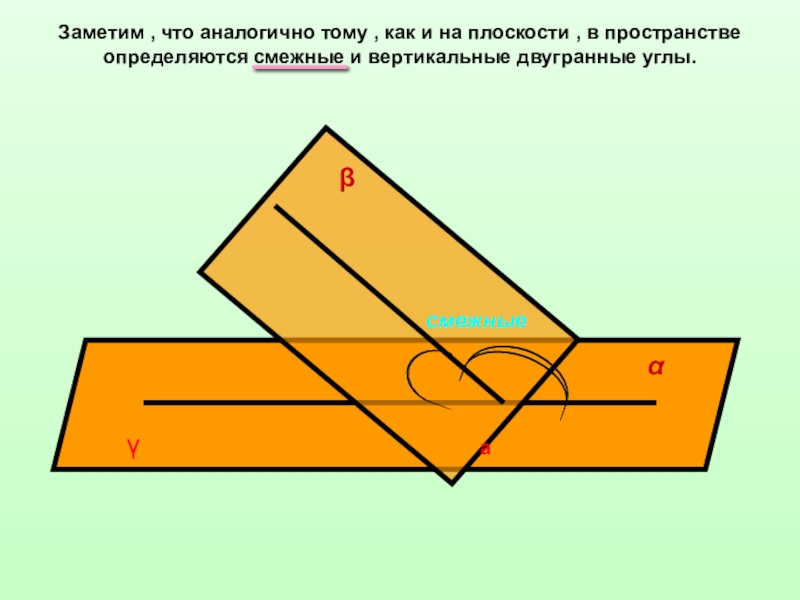
- 13. Заметим , что аналогично тому , как
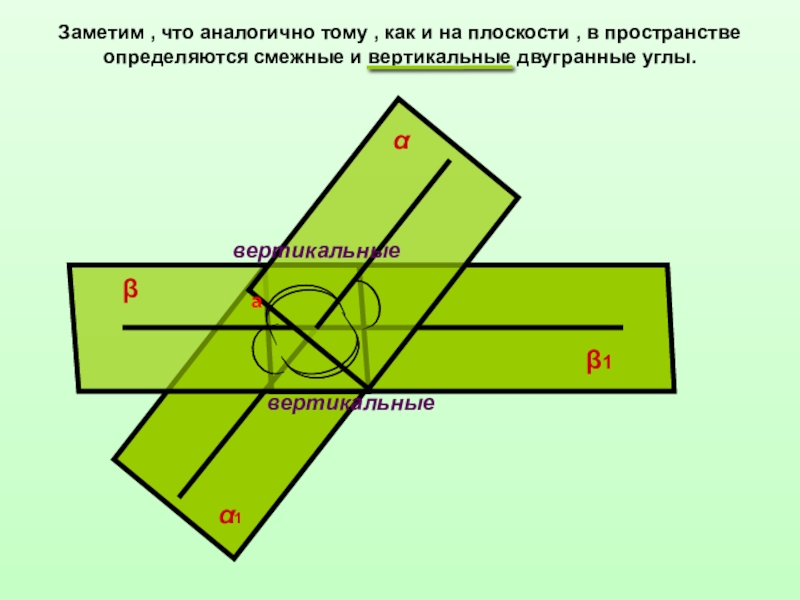
- 14. Заметим , что аналогично тому , как
- 15. Определение : Углом между двумя пересекающимися плоскостями
- 16. ββ1аαα1сϕВеличина угла между плоскостями принадлежит промежутку [0°;90°].
Вопрос № 1.Сформулируйте теорему о трёх перпендикулярах.
Слайд 1Двугранный угол
Что называют углом между пересекающимися прямыми?
Что называют углом между прямой
Слайд 3Вопрос №2.
Постройте куб АВСДА¹В¹С¹Д¹(1вариант) и МNOPM¹N¹O¹P¹( 2вариант).
Укажите проекцию диагонали АС¹ на
АВСД(1вар) и N¹Р на МNOP(2 вар).
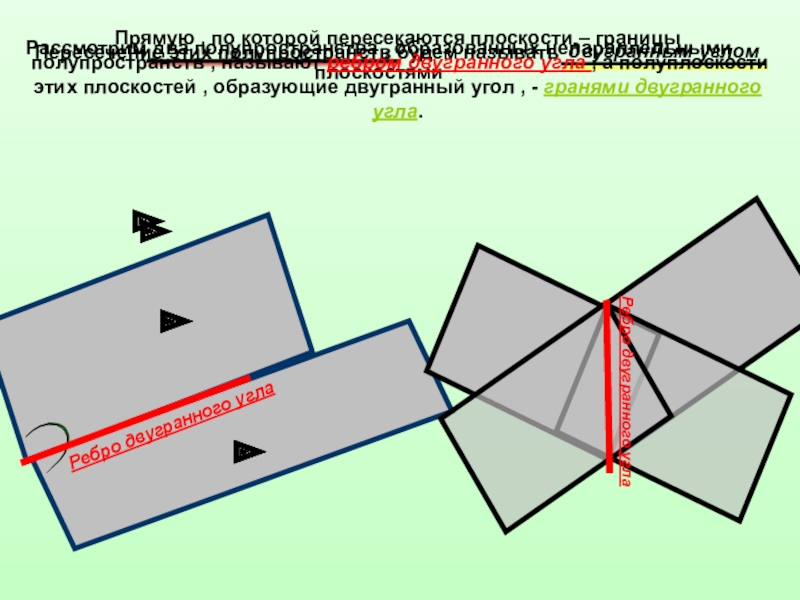
Слайд 4Рассмотрим два полупространства , образованных непараллельными плоскостями
Пересечение этих полупространств будем
называть
двугранным углом
Прямую , по которой пересекаются плоскости – границы полупространств , называют ребром двугранного угла , а полуплоскости этих плоскостей , образующие двугранный угол , - гранями двугранного угла.
Ребро двугранного угла
Ребро двугранного угла
Слайд 5
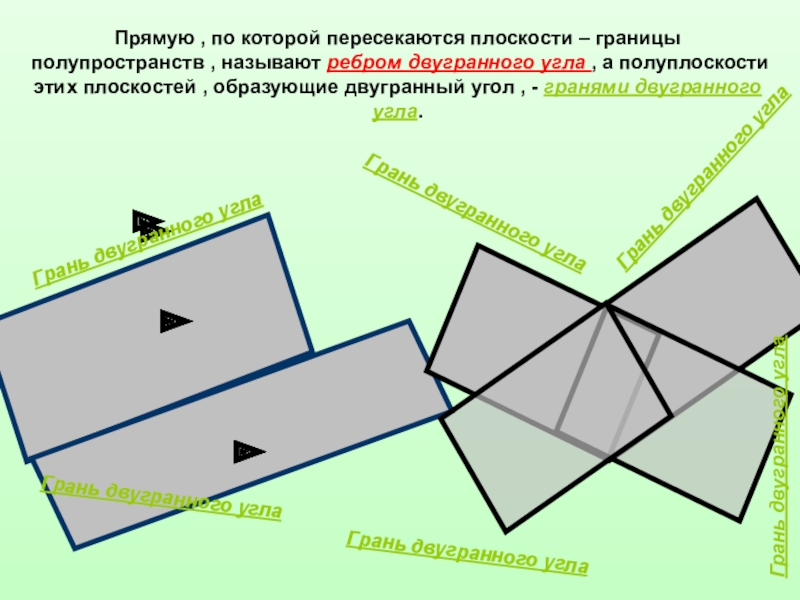
Прямую , по которой пересекаются плоскости – границы полупространств , называют
ребром двугранного угла , а полуплоскости этих плоскостей , образующие двугранный угол , - гранями двугранного угла.
Грань двугранного угла
Грань двугранного угла
Грань двугранного угла
Грань двугранного угла
Грань двугранного угла
Грань двугранного угла
Слайд 6
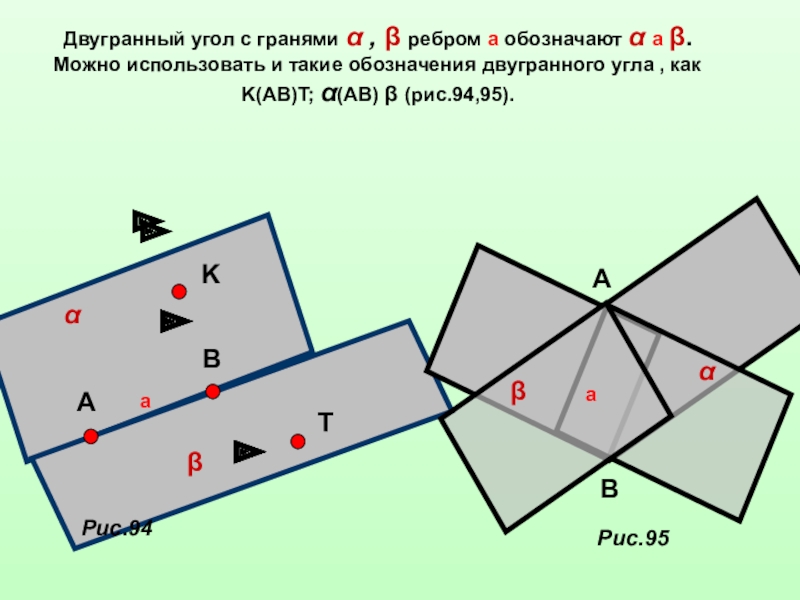
Двугранный угол с гранями α , β ребром а обозначают α
а β.
Можно использовать и такие обозначения двугранного угла , как
K(AB)T; α(AB) β (рис.94,95).
Можно использовать и такие обозначения двугранного угла , как
K(AB)T; α(AB) β (рис.94,95).
Рис.94
Рис.95
Слайд 7
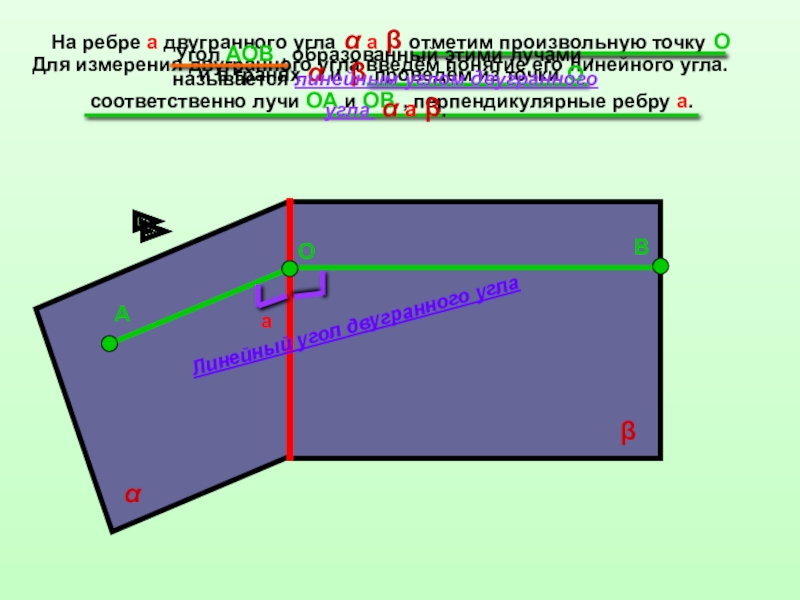
Для измерения двугранного угла введём понятие его линейного угла.
На ребре а
двугранного угла α а β отметим произвольную точку O и в гранях α и β проведём из точки O
соответственно лучи ОА и ОВ , перпендикулярные ребру а.
соответственно лучи ОА и ОВ , перпендикулярные ребру а.
а
α
β
О
А
В
Угол АОВ , образованный этими лучами , называется линейным углом двугранного угла α а β.
Линейный угол двугранного угла
Слайд 8
а
α
β
О
А
В
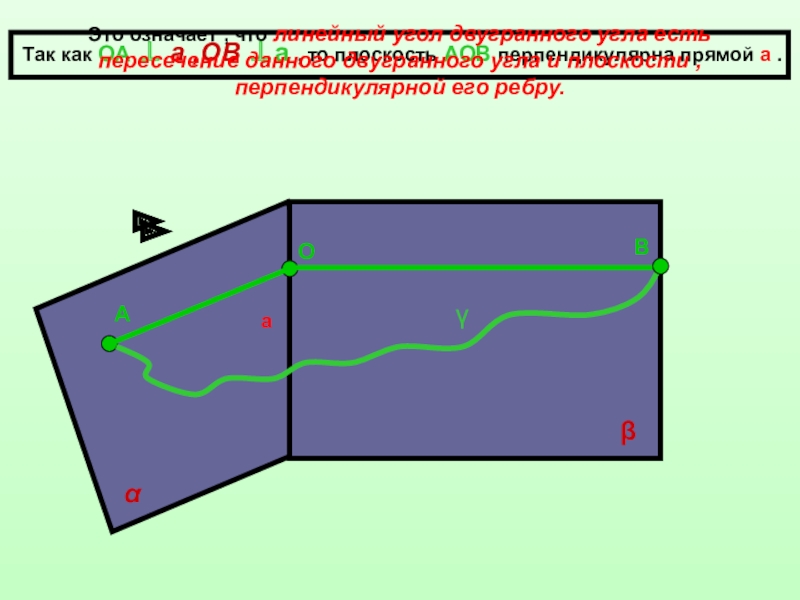
Так как ОА ⊥ а ,ОВ ⊥а , то плоскость АОВ
перпендикулярна прямой а .
γ
Это означает , что линейный угол двугранного угла есть пересечение данного двугранного угла и плоскости , перпендикулярной его ребру.
Слайд 9
Теорема : Величина линейного угла не зависит от выбора его вершины
на ребре двугранного угла.
Определение : Величиной двугранного угла называется величина его линейного угла.
Величина двугранного угла (измеренная в градусах ) принадлежит промежутку (0°;180°).
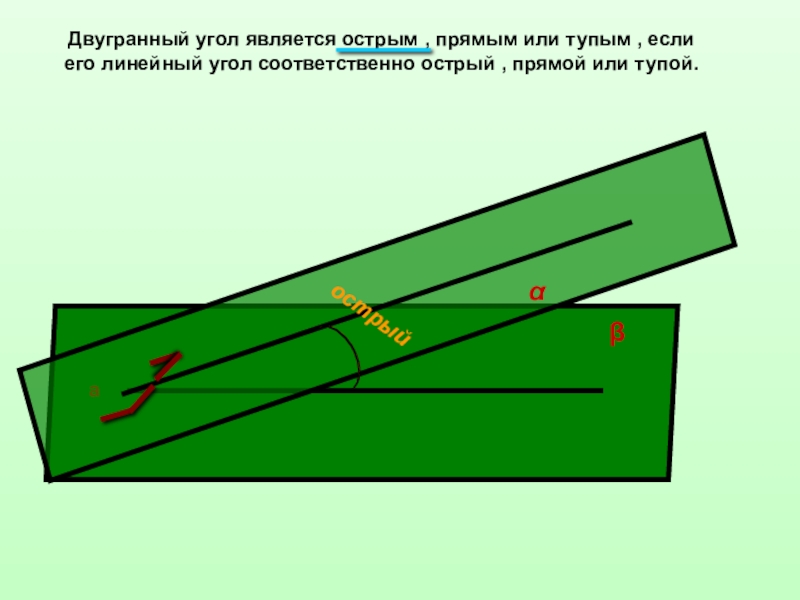
Слайд 10Двугранный угол является острым , прямым или тупым , если его
линейный угол соответственно острый , прямой или тупой.
острый
Слайд 11
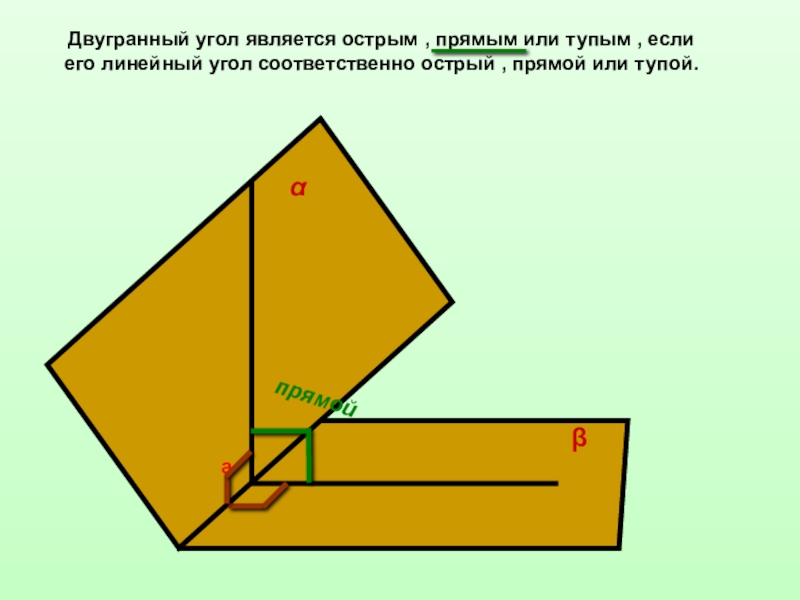
Двугранный угол является острым , прямым или тупым , если его
линейный угол соответственно острый , прямой или тупой.
прямой
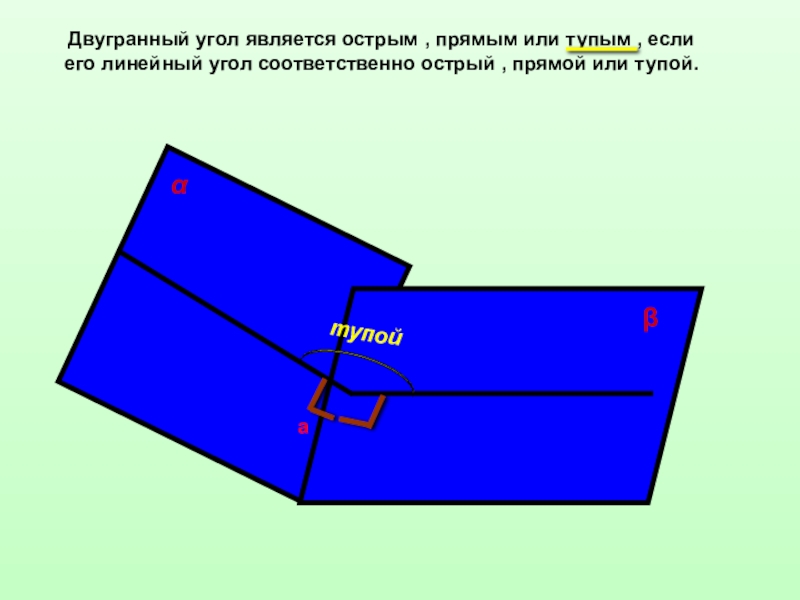
Слайд 12Двугранный угол является острым , прямым или тупым , если его
линейный угол соответственно острый , прямой или тупой.
тупой
Слайд 13Заметим , что аналогично тому , как и на плоскости ,
в пространстве определяются смежные и вертикальные двугранные углы.
Слайд 14Заметим , что аналогично тому , как и на плоскости ,
в пространстве определяются смежные и вертикальные двугранные углы.
β
β1
а
α
α1
Слайд 15Определение : Углом между двумя пересекающимися плоскостями называется наименьший из двугранных
углов , образованных при их пересечении.
Угол между параллельными или совпадающими плоскостями полагается равным нулю.
![ββ1аαα1сϕВеличина угла между плоскостями принадлежит промежутку [0°;90°].](/img/tmb/7/679695/8dd722a1e0af147a080fb7f5b9144e0c-800x.jpg "Презентация по геометрии на тему Двугранный угол ββ1аαα1сϕВеличина угла между плоскостями принадлежит промежутку [0°;90°].")
